Les lois de la gravitation énoncées par en 1687 représentent une
rupture dans l’évolution des idées en physique. Newton fût en effet un
acteur important de la révolution scientifique qui eut lieu entre le
XVIIᵉ et le XVIIIᵉ siècle. Héritier direct de (entre autres) Descartes,
Galilée, Brahé ou Copernic, Newton se nourrit
de leurs travaux et des observations de Kepler pour élaborer une théorie mathématique permettant
d’expliquer les phénomènes observés. Ce sont ces deux aspects – la
mathématisation de la physique d’une part, et de sa théorie d’autre part – qui représentent
une révolution dans l’évolution des idées en physique et qui auront une
influence profonde pour les siècles à venir, jusqu’à aujourd’hui.
Les anciens (depuis Aristote jusqu’à Galilée) avaient rapidement
pressenti que les mathématiques pouvaient être l’outil ultime pour
modéliser les phénomènes observés et ainsi écrire le « grand livre de la
Nature ». Mais Newton est véritablement le premier à mettre en oeuvre et
réussir la mathématisation de lois de la physique. Avec ses travaux, il
montre que la physique ne se limite pas aux observations, mais que tout
peut être traduit en langage mathématique.
L’universalité de sa théorie, qui permet d’expliquer aussi bien les
phénomènes célestes (mouvements des planètes, mouvements des lunes,
comètes)
que les phénomènes terrestres (chute des objets, par exemple
une pomme), était également nouveau à une époque où l’on se contentait
d’expliquer les phénomènes de manière « locale » et individuelle.
L’universalité devînt dès lors la quête ultime des physiciens
développant de nouvelles théories, depuis Fourier, Maxwell, Einstein
etc… jusqu’à nos jours puisque la recherche d’une grande théorie du
Tout unifiant l’ensemble des interactions fondamentales restent une des
plus grandes préoccupations de la science moderne.
L’histoire de la chute d’une pomme qui aurait inspiré sa théorie à
Newton n’est qu’un épisode d’une histoire beaucoup plus riche et
illustratrice de l’effervescence scientifique à cette époque. Le premier à émettre l’hypothèse que la force d’attraction des corps
suit une loi inversement proportionnelle au carré de la distance est
apparemment Robert Hooke, un
scientifique contemporain de Newton. Mais
malgré ses efforts, celui-ci n’arrive pas à démontrer son hypothèse. Sir
Edmond Halley, un riche scientifique resté dans l’histoire pour avoir
calculé l’orbite de la comète du même nom, est passionné par cette
question et offre un prix à celui qui pourra en faire la démonstration.
Après plusieurs années sans que personne ne trouve de solution, Halley
contacte Isaac Newton à Cambridge en 1684 pour lui présenter le
problème. Newton est immédiatement fasciné par la question. Grâce à
l’aide financière de Halley il va travailler d’arrache pied pendant
trois ans (durant lesquels aura lieu l’épisode de la pomme) pour publier
en 1687 ses fameux ouvrages Philosophiae naturalis principia mathematica
La loi de la gravitation stipule que deux objets massifs interagissent à
distance par l’intermédiaire d’une force qui est toujours attractive.
Cette loi prend une forme simple dans le cas de deux sphères uniformes,
ou encore dans le cas de deux corps de forme quelconque mais dont les
dimensions sont suffisamment réduites pour qu’ils puissent être
considérés comme ponctuels vis-à-vis de la distance qui les sépare.
Le raisonnement qui a conduit Newton à la découverte de la loi de la
gravitation est basé sur les hypothèses suivantes:
le corps \(A\) exerce sur le corps \(B\) une force proportionnelle à la quantité de matière qui compose le corps \(A\). Autrement dit, la force est proportionnelle à la masse du corps\(A\).
d’après le principe des actions réciproques, la force exercée par \(B\) sur \(A\) doit être de même intensité mais de sens opposé à la force de \(A\) sur \(B\). Il en découle donc que la force de gravitation est également proportionnelle à la masse du corps\(B\).
enfin, l’intensité de la force diminue avec la distance séparant les centres de masse des deux corps. Pour que l’expression soit compatible avec les lois phénoménologiques établies par Kepler (1571–1630), Newton conclut que la force gravitationnelle doit être inversement proportionnelle au carré de la distance.
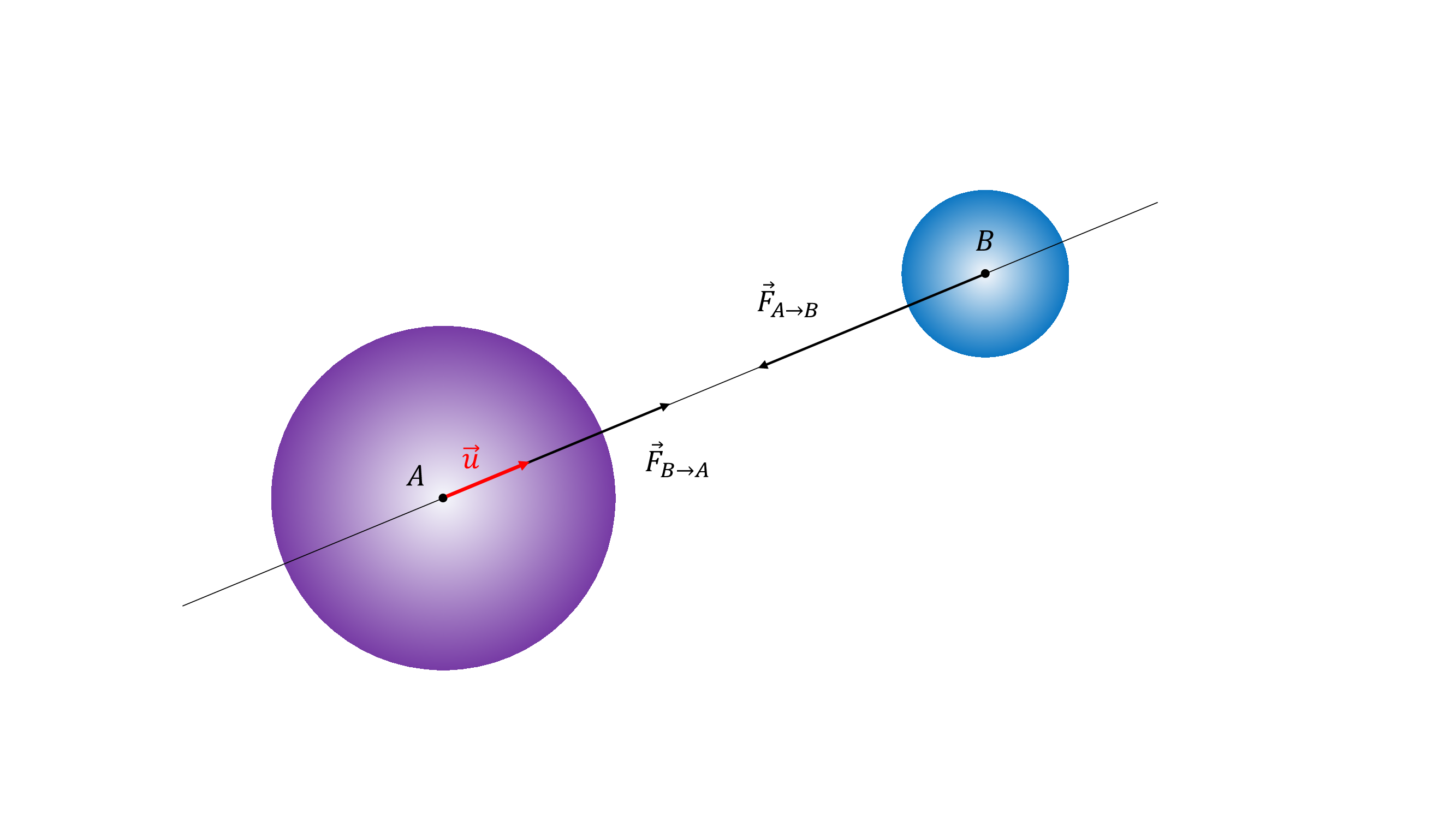
Fig. 16 Deux corps massifs s’attirent selon la loi universelle de la gravitation.
Loi
Loi universelle de la gravitation
Deux corps de masse \(m_A\) et \(m_B\), dont les centres de gravité \(A\) et \(B\) sont séparés de la distance \(r\), exercent l’un sur l’autre la force gravitationnelle :
avec \(\vec{u}=\overrightarrow{AB}/\Vert \overrightarrow{AB} \Vert\) est le vecteur unitaire de la droite \((AB)\) — voir la Fig. 16 — et \(\mathcal{G}\) la constante gravitationnelle : \(\mathcal{G} \approx 6.67\times10^{-11}~\text{N} \cdot \text{m}^{2} \cdot \text{kg}^{-2}\).
Étant donnée la valeur très faible de \(\mathcal{G}\), la force d’attraction entre deux objets de masses usuelles est donc négligeable.
Un peu d’Histoire… l’expérience de Cavendisch
Isaac Newton ne réussi pas à mesurer la constante \(\mathcal{G}\). C’est Henry Cavendish (1731–1810) qui la mesura pour la première fois. Pour ce faire, il utilisa une balance de torsion avec deux boules en plomb de masse m placées le long d’une tige horizontale (Fig. 17, boules jaunes). La connaissance du moment d’inertie de l’ensemble tige+boules et de la constante de torsion du fil de suspension permet de prédire la fréquence des oscillations de la balance. La très faible attraction gravitationnelle causée par deux autres boules de plomb (boules grises), placées indépendamment à l’extrémité de la balance, cause une légère modification des oscillations, et permet de calculer la force de gravité entre les boules, et ainsi la valeur de la constante de gravitation \(\mathcal{G}\). Le dispositif a été largement amélioré depuis les travaux de Cavendish : en 2021, des scientifiques sont parvenus à mesurer l’interaction gravitationnelle entre deux billes de masse \(m\simeq 90\) mg.
L’excellent blog de Walter Bislin propose une simulation numérique de l’expérience et reprend l’analyse mathématique détaillée du problème.
Fig. 17 Balance de torsion utilisée par Cavendish pour mesurer \(\mathcal{G}\).
Application 5.1: Calculer la force gravitationnelle entre deux billes d’or de rayon \(a=1\) mm séparées de la distance \(d=5\) mm. On donne la masse volumique de l’or : \(\rho=19,3~\text{g}\cdot \text{cm}^{-3}\).
Calculons la masse d’une bille: elle est donnée par le volume de la bille multiplié par la masse volumique:
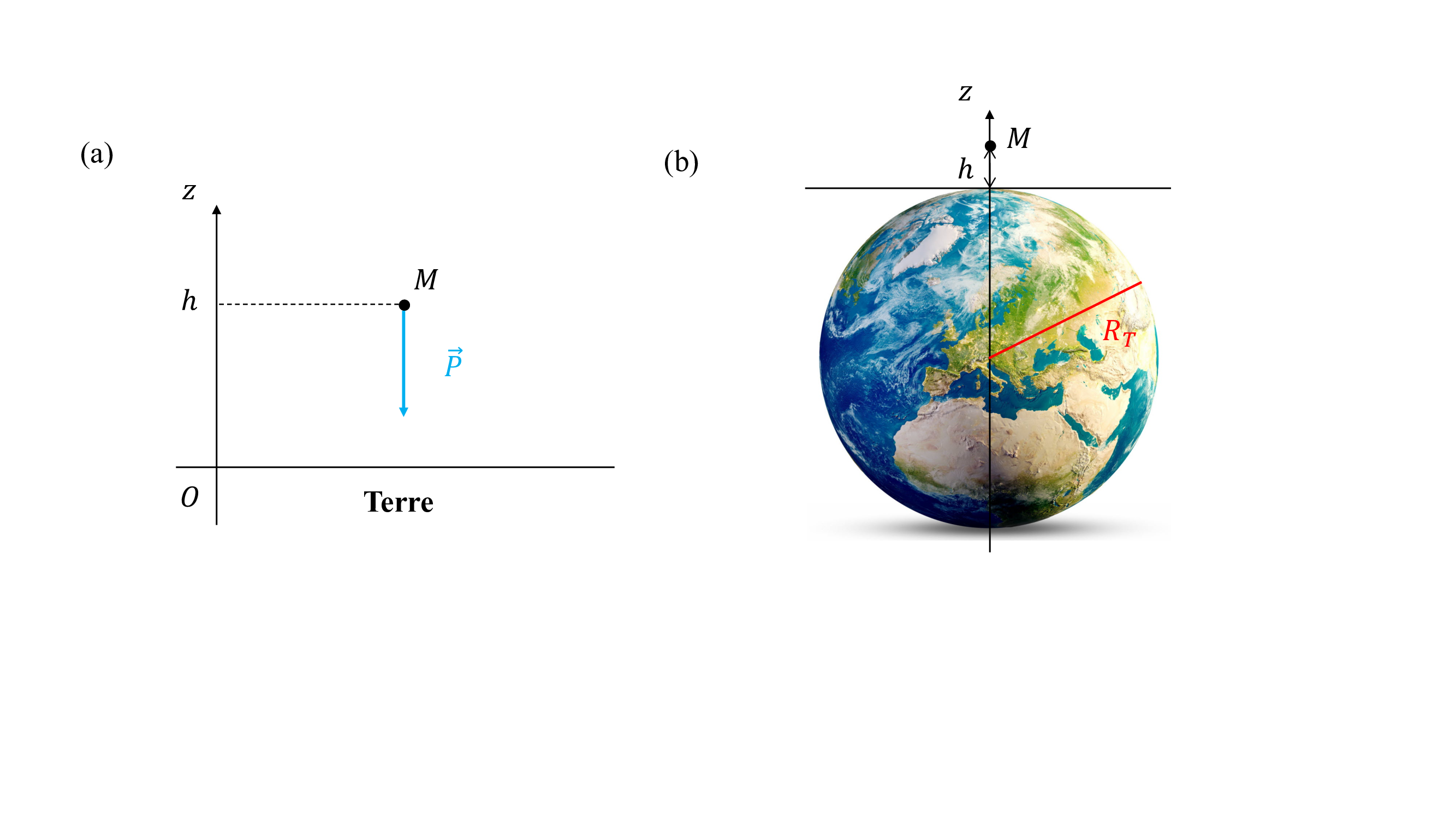
Fig. 18 Le poids (a) et la force gravitationnelle (b) sont deux manifestations de la même force.
Comparons à présent les deux situations présentées sur la Fig. 18. Précédemment, nous avons vu qu’un objet de masse \(m\) est soumis à la surface de la Terre à son poids :
où \(g\) est l’accélération de la pesanteur. D’un autre côté, la loi
universelle de la gravitation énonce qu’un objet de masse \(m\)
située à l’altitude \(h\) par rapport à la surface de la Terre est
attiré par la force gravitationnelle \(\vec{F}\):
où \(m_T\) est la masse de la Terre et \(R_T\) son rayon. Or
d’après Newton, ces deux forces sont l’expression d’une seule et unique interaction. En comparant les équtions (48) et (49), nous pouvons directement déduire que
l’accélération de la pesanteur est donnée par :
Arrêtons-nous quelques instants pour commenter la relation (50):
l’accélération de la pesanteur est indépendante de la masse de l’objet qui subit la force. Deux corps de masses différentes en chute libre mettrons donc la même durée pour atteindre le sol.
l’attraction gravitationnelle diminuant avec la distance, il en résulte que \(g\) décroît à mesure que l’altitude augmente. Cependant, le rayon de la Terre étant de plusieurs milliers de km, cette variation reste très faible pour des altitudes \(h \ll R_T\).
La théorie de Newton permet ainsi de calculer la valeur de \(g\) à la surface de la Terre (\(h=0\)) :
Une autre conséquence de la relation (50) est que le poids d’un objet varie d’un astre à l’autre. Considérons par exemple la
Lune : en appliquant la formule (50) avec les valeurs numériques \(m_L \approx 7,35 \times 10^{22}\) kg et
\(R_L \approx 1736~\)km, on obtient : \(g_L \approx 1,63~\text{m}\cdot \text{s}^{-2}\). La gravité est
donc environ 6 fois plus faible sur la lune que sur la Terre, comme illustré sur la Fig. 19 (a).
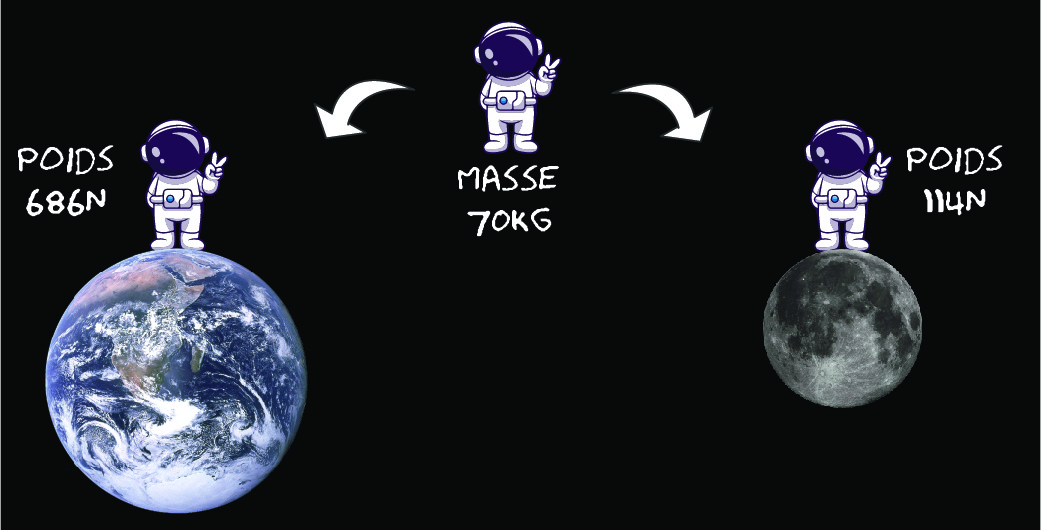
Fig. 19 Le poids d’un astronaute de 70kg est de 686 N sur la Terre, contre seulement 114 N sur la Lune.
Enfin, notons encore que la détermination précise de \(g\) est
rendue complexe par le fait que la Terre n’est ni pas parfaitement
sphérique, ni parfaitement homogène. La valeur de \(g\) varie donc
légèrement d’un endroit à un autre — voir la Fig. 20.
Pour les besoins pratiques, la Conférence générale des poids et mesures a défini en 1901 une valeur normale de l’accélération de la pesanteur, à l’altitude 0, sur un ellipsoïde idéal approchant la surface terrestre, pour une latitude de 45°, égale à 9.80665 m s⁻², souvent approximé à 9.81 m s⁻².
Pour comprendre le mouvement orbital d’un satellite autour d’une planète
ou d’une planète autour d’une étoile, revenons sur le principe d’inertie
qui peut s’énoncer ainsi :
« Tout corps persévère dans son état de repos ou de mouvement uniforme
en ligne droite, à moins qu’il ne soit contraint, par des forces
s’imprimant sur lui, à changer cet état. »
De fait, une trajectoire circulaire implique la présence d’une force qui
empêche le corps de poursuivre son mouvement « naturel » rectiligne. Sur
l’illustration de gauche de la Fig. 21, une
personne fait tourner un ballon au bout d’une corde. La force de tension
permet de maintenir le ballon sur la trajectoire circulaire. Si la corde
casse, la force de tension s’annule et le ballon poursuit son mouvement
selon une trajectoire rectiligne, conformément au principe d’inertie.
En énonçant le premier principe de la dynamique, Galilée puis Newton firent le constat que le mouvement circulaire n’était pas un mouvement « naturel », puisque d’après ce principe les seuls mouvements « naturels » (c’est à dire en l’absence de force) sont le repos (absence de mouvement) et le mouvement rectiligne uniforme. Dès lors, le mouvement circulaire (qui jusqu’alors était considéré comme un mouvement naturel) impliquait l’existence de forces pour contraindre les objets sur leurs trajectoires.
Dans le cas des astres, c’est la force de gravité qui empêche la Lune ou
les satellites artificiels de s’échapper de leur trajectoire circulaire,
tout comme la corde empêche le ballon de continuer en ligne droite
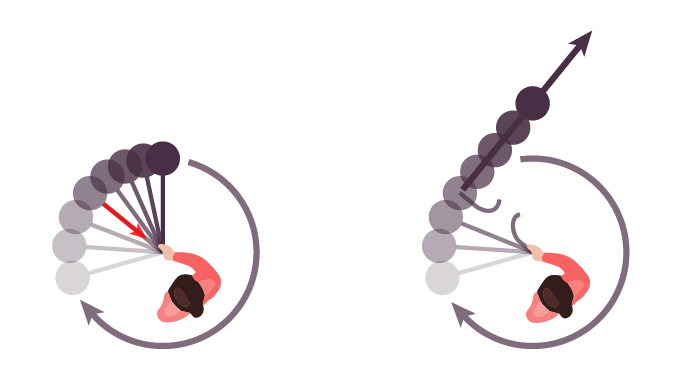
Fig. 21 Le mouvement circulaire implique l’existence d’une force centripète.
Nous avons établi au Chapitre 2 que le mouvement circulaire uniforme est
un mouvement uniformément accéléré : la norme \(v\) du vecteur vitesse est constante mais sa direction change à tout instant. Le
vecteur accélération est centripète, c’est-à-dire orienté vers le centre du cercle :
Il peut sembler contre-intuitif qu’un objet dont la norme de la vitesse est constante soit en fait accéléré à tout instant.
On sait qu’en physique un changement du vecteur vitesse est par définition appelé une accélération. Ce changement peut intervenir sur la norme du vecteur, sur sa direction, ou sur les deux.
Dans le mouvement circulaire uniforme, la norme du vecteur vitesse est constante mais sa direction change à tout instant. Le mouvement circulaire uniforme est donc un mouvement en accélération continue.
On peut l’expliquer en considérant la variation de vitesse entre deux instants: la Fig. 22 illustre l’accélération centripète. À tout instant, la vitesse d’un objet en mouvement circulaire uniforme est perpendiculaire au mouvement. Entre deux positions 1 et 2:
la norme reste constante \(||\vec{v_{1}}||=||\vec{v_{2}}||\)
l’orientation du vecteur vitesse varie, et cette variation s’exprime comme \(\Delta \vec{v}=\vec{v_{2}}-\vec{v_{1}}\)
On voit que la variation de vitesse \(\Delta \vec{v}\) entre ces deux points est orientée vers le centre du cercle qui constitue l’orbite.
Or une variation de vitesse n’est rien d’autre qu’une accélération, et l’on voit dans la Fig. 22 que cette accélération est centripète.
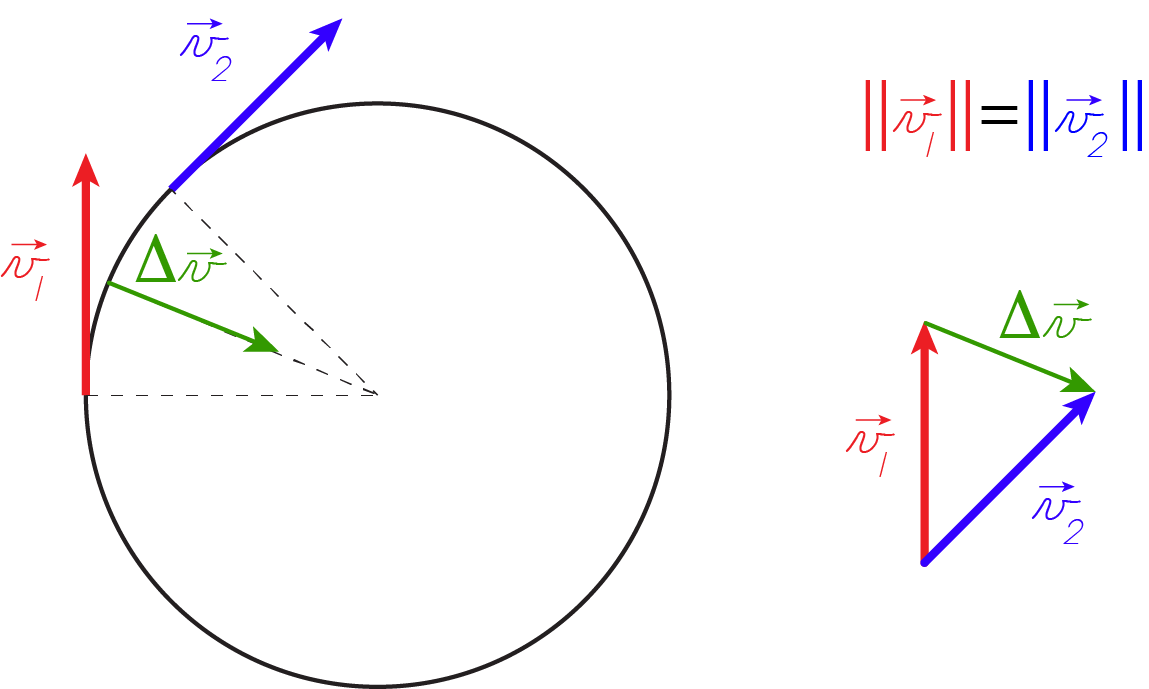
Fig. 22 Le mouvement circulaire uniforme est un mouvement accéléré, avec une accélération centripète.
D’après le principe fondamental de la dynamique,
l’intensité \(F_c=\Vert \vec{F}_c \Vert\) de la force centripète
associée à cette accélération est alors égale à : \(F_c=ma_c\).
Dans le cas des astres, c’est la gravité qui empêche à tout instant la
Lune ou les satellites artificiels de s’échapper de leur trajectoire
circulaire, tout comme la corde empêche le ballon de continuer en ligne
droite (Fig. 23).
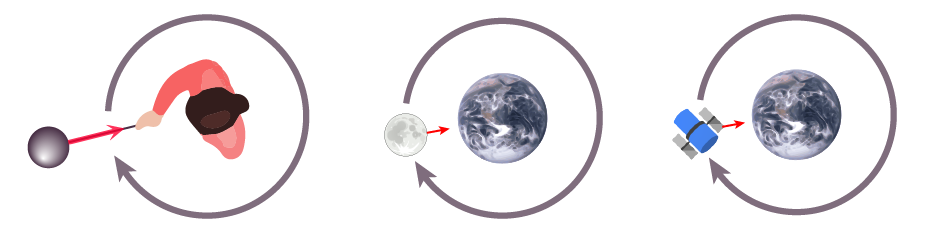
Fig. 23 La Lune et les satellites artificiels suivent des trajectoires
circulaires autour de la Terre car ils sont soumis à une force
centripète.
Mais qu'est ce qui empêche les satellites (naturels ou artificiels) de retomber sur Terre sous l’effet de la gravité?
Pour répondre à cette question, il faut commencer par comprendre comment les satelites artificiels sont placés sur orbite.
Qu’est ce qui empêche un satellite (naturel ou artificiel) de retomber sur Terre sous
l’effet de la gravité ? Pour répondre à cette question, il faut d’abord
comprendre comment les satellites artificiels sont placés sur orbite.
Newton a imaginé pour cela l’expérience de pensée illustrée par les figures ci-dessous: on place un canon sur la plus haute
montagne de la Terre, les boulets étant soumis uniquement à la gravité.
Expérience (a)
Expérience (b)
Expérience (c)
Expérience (d)
Cette exercice de pensée naïf nous montre qu’il existe une vitesse minimale permettant de compenser l’attraction gravitationnelle. Contrairement à une idée répandue, le boulet n’est pas en impesanteur. On comprend également qu’un satellite est en permanence en train de retomber sur la Terre, mais il est maintenu sur sa trajectoire circulaire par son inertie.
En principe, il serait possible de placer des satellites en orbite à
n’importe quelle altitude. Néanmoins, la dissipation d’énergie due aux
frottements avec l’air de l’atmosphère empêchent de placer un satellite
à moins de \(\approx 200\) km d’altitude. À titre d’exemple, les satellites Starlink ou encore le téléscope spatial Hubble sont sur des orbites situées autour de 550km, tandis que la station spatial internationale se trouve à une altitude moyenne de 400km.
L’applet ci-dessous vous permet de suivre la position de la station spatiale internationale (ISS) et du télescope spatiale Hubble (HST) en temps réel.
Trouvons l’expression de la vitesse de satellisation par analyse dimensionnelle.
Identification des paramètres importants
Puisque la force impliquée dans notre problème est la gravité, on peut raisonnablement supposer que la vitesse en question dépendra de:
\(m_{\rm T}\) la masse de la Terre
\(\mathcal{G}\) la constante de la gravitation
\(R\) l’altitude du satellite (définie ici comme la distance au centre de la Terre, et non pas à la surface de la Terre)
Précisons les dimensions de chacun des paramètres importants que nous venons d’identifier:
\(R\) est une distance et a donc la dimension d’une longueur \(L\)
\(v\) est une vitesse et a la dimension d’une longueur divisée par une durée \(L T^{-1}\)
\(m_{\rm T}\) est une masse et a la dimension d’une masse \(M\)
La dimension de la constante de la gravitation \([\mathcal{G}]\) n’est pas triviale. On peut facilement la déterminer en utilisant la loi de la gravitation de Newton. Les dimensions doivent être égale de chaque côtés de l’équation:
Nous pouvons maintenant être plus quantitatif en trouvant l’expression exacte et complète de la vitesse
d’un satellite sur une orbite circulaire de rayon \(R\). Pour cela,
on applique bien sûr le principe fondamental de la dynamique à un point matériel
de masse \(m\) soumis à la force de gravitation (47). Étant donné
l’expression (51) de l’accélération, on obtient :
la constante qui nous manquait dans l’analyse dimensionnelle vaut simplement 1.
Cette vitesse est indépendante le la masse du satellite : cela signifie qu’à altitude égale, un petit satellite de quelques kilogrammes comme CubeSat aura la même vitesse que la station spatiale internationale qui pèse 450 tonnes.
Pour aller plus loin: Comment les planètes ont-elles acquis la vitesse nécéssaire pour être en orbite autour du Soleil?
Les planètes se forment dans le disque de poussière (disque proto-planétaire) qui entourait le Soleil dans sa jeunesse. À cause de la gravitation et des asymétries dans le nuage de poussière originel, ce disque était en rotation. Les planètes qui s’y sont formé ont hérité de cette rotation. Il est fort probable que de nombreuses autres planètes se soient formées au début de la vie du Soleil, certaines ayant été « avalées » par le Soleil car leurs vitesses n’étaient pas suffisante et d’autres ayant été éjectées dans l’espace intersidéral car leurs vitesses étaient trop importantes. Les interactions gravitationnelles entre planétésimaux peuvent en effet modifier leurs vitesses et provoquer des migrations et des éjections.
Application 5.2: La station spatiale internationale (ISS) est en orbite autour de la Terre à une altitude moyenne de 400 km. Calculer la vitesse de l’ISS. Quelle est la période de l’orbite ?
On rappelle:
la masse de la Terre \(5.97\times10^{21}\) tonnes
le rayon de la Terre: 6371 km
la valeur de \(\mathcal{G}=6.67\times10^{-11} N m^{2} kg^{-2}\)
à 400km: on a alors \(R=6371\times10^{3} + 400\times10^{3} = 6771\times10^{3}~m\)
De la même manière on peut s’amuser à calculer à quelle vitesse nous nous déplaçons sutour du Soleil: la Terre tourne autour du Soleil sur une trajectoire à peu près circulaire de 150 000 000 km de rayon en 365.25 jours.
On peut en déduire que la vitesse de révolution vaut:
\[v=\frac{2\pi \times 150\times10^{9}}{365.5\times24\times3600}=29865 m\cdot s^{-1} = 170515 km \cdot h^{-1}\]
Pour certaines applications (télécommunications, météorologie, …), il
est nécessaire que l’orbite du satellite soit synchronisée avec le
mouvement de rotation de la Terre. Depuis la surface de la Terre, le
satellite semble fixe : on parle de satellite géostationnaire. Or la
vitesse — et donc que la période — d’un satellite ne dépend que du rayon
de son orbite. Il existe donc une altitude unique, située à près de 36
000 km de la surface de la Terre, appelée orbite géostationnaire.
Cette altitude très spéciale est donc évidemment très prisée par les différents acteurs de la conquête spatiale: les états et les entreprises en ont besoin pour les communications (téléphonie, internet, télévision), les militaires et les scientifiques pour l’observation de la Terre en continue. Il y a environ 22 000 satellites géostationnaires actuellement en orbites!
Fig. 24 Orbite géostationnaire: la période du satellite étant synchronisé avec celle de la Terre, celui-ci observe toujours la même partie de la Terre. Crédit: NASA.
Historiquement, Newton a utilisé les lois empiriques de Kepler pour
mettre au point sa théorie de la gravitation. Ici, nous menons le
raisonnement inverse afin de démontrer la troisième loi de Kepler
relative au mouvement des planètes :
« Le carré de la période de révolution est proportionnel au cube de la distance au Soleil ».
Pour établir cette loi, notons tout d’abord que la vitesse \(v\)
d’une planète sur une orbite circulaire de rayon \(R\) est reliée à
sa période \(T\) :
\[v = \frac{2 \pi R}{T} \ .\]
Si l’on compare à l’expression (53) on obtient donc
directement la troisème loi de Kepler:
Loi
Troisième Loi de Kepler.
Le carré de la période de révolution T d’un corps en
orbite autour d’un astre de masse M est
proportionnel au cube du rayon R de sa trajectoire
La Figure interactive ci-dessous présente la période observée pour les 8 planètes du système solaire ainsi que Pluton en fonction du rayon observé de leur orbite, et compare avec la prédiction théorique de la Troisième Loi de Kepler. On voit que les mesures sont en excellents accord (zoomez pour mieux voir sur le planètes telluriques).
La théorie de Newton permet donc de démontrer la loi que Kepler avait
établie de manière empirique à partir des mesures de la position des
planètes, réalisées en particulier par l’astronome danois Tycho
Brahe (1546-1601). Il
devient ainsi possible d’expliquer et de prédire avec précision les
paramètres orbitaux de tous les astres (planètes, satellites, comètes)
du système solaire. Notons cependant que nous avons restreint la
discussion aux seules orbites circulaires : en fait, une étude plus
approfondies des équations du mouvement montrent que les trajectoires
sont des coniques : ce sont soit des ellipses (dont le cercle est un
cas particulier), soit des hyperboles, soit des paraboles.
Un peu d’Histoire…
Les lois de Kepler, et donc les lois de Newton dont elles découlent, permettent donc d’expliquer et de prédire avec une précision redoutable les paramètres orbitaux de toutes les planètes et satellites du système solaire. Toutes? Alors que les mesures s’affinaient grâce à l’amélioration des instruments, les astrophysiciens de la fin du XIXème siècle se rendirent compte que Mercure posait problème: les lois de Newton ne permettaient pas de prédire correctement son orbite et il y avait un décalage de quelques secondes d’arc par siècle. On parla alors de l”anomalie de Mercure. Par analogie avec l’anomalie de l’orbite d’Uranus, qui avait mené l’astronome Le Verrier à prédire l’existence et la position de Neptune, les astronomes supposèrent que l’anomalie de Mercure était sans doute dûe à la présence d’une autre planète inconnue (qu’ils appelèrent Vulcain) et qui perturberait le mouvement de cette dernière. Malgré leurs efforts les astronomes ne purent jamais observer Vulcain, même si certains prétendaient l’avoir vue sans fournir de preuves.
En 1916, Albert Einstein énonce la théorie de la relativité générale, qui revisite et explique la gravitation non plus comme une force mais comme une déformation de l’espace-temps. La théorie d’Einstein montre en particulier que des effets non-prévus par la théorie Newtonienne apparaissent au voisinage de corps de masses très importantes, comme le Soleil. En appliquant sa théorie au mouvement de Mercure, Einstein fournit l’explication du décalage observé avec une précision remarquable.
Pourquoi seule l'orbite de Mercure est affectée?
En fait la relativité générale s'applique à toutes les planètes du système solaire, mais la correction par rapport à la théorie Newtonienne n'est significative que dans le cas de Mercure, qui est la planète la plus proche du Soleil.
Malgré ce résultat, une partie de la communauté était toujours sceptique vis à vis de la théorie révolutionnaire d’Einstein. L’astronome anglais Arthur Eddington profite d’une éclipse de soleil le 29 mai 1919 pour apporter la preuve expérimentale de la théorie d’Einstein en observant l’effet de lentille gravitationnelle produit par le Soleil sur les étoiles situées derrière lui. Le film « Einstein et Eddington » sorti en 2008 raconte l’histoire de l’expérience d’Eddington.
De la même manière, sans la prise en compte des effets relativistes les satellites de géopositionnement comme GPS ou Galiléo auraient une précision de l’ordre de plusieurs kilomètres, au lieu de quelqiues centimètres!
Kepler s'est basé sur les observations des planètes du systèmes solaires pour construire sa loi empirique.
Oui, c'est bien cela
Mais alors cette loi est-elle valable pour d'autres systèmes planétaires, au-delà du système solaire?
Vérifions le expérimentalement pour un système d'exoplanètes!
Nous allons étudier le système d”exo-planètes orbitant l’étoile naine rouge TRAPPIST 1 de masse \(M=1.78\times10^{29}\) kg.
Ce système possède 7 planètes dont les périodes ont été mesurées avec précision par la méthode des transits.
Les données de ces exo-planètes sont les suivantes (on considère en première approximation que leurs orbites sont circulaires):
On confirme donc que la Troisième Loi de Kepler est valide pour un système d’exoplanètes quelconque!
Nous savions que les lois de Newton dont découle la Troisième Loi de Kepler sont en effet universelles et s’appliquent partout dans l’Univers (sauf lorsque l’environnement est relativiste).
Pour aller plus loin: TRAPPIST-1 au Laboratoire d’Astrophysique de Bordeaux
La figure Fig. 25 ci-dessous a fait la couverture de la revue Nature. Elle représente le système planétaire TRAPPIST 1 et illustre les propriétés remarquables de ces exo-planètes.
Premièrement on voit que l’étoile est très rouge: c’est en effet une naine ultra-froide, dont la température atteind seulement 2500K (comparée aux 5800K du Soleil).
Les planètes sont entre 20 et 100 fois plus proches de leur étoile que ne l’est la Terre du Soleil.
Les deux premières planètes (b et c) sont très proches de l’étoile, trop proches pour que l’eau existe sous forme liquide. L’artiste a donc representé de la vapeur d’eau autour des orbites de ces planètes.
La dernière planète (h) est quant à elle tellement éloignée de son étoile qu’elle ne recoit pas suffisamment de chaleur pour que l’eau existe sous forme liquide. L’artiste a donc representé des cristaux de glace au-delà de son orbite.
Les 4 autres planètes (d,e,f,g) sont en revanche à des distances intermédiaires qui, selon les estimations des astrophysiciens, pourraient permettre l’existence d’eau liquide. Cette zone très particulière défini la zone d’habitabilité, car la vie telle qu’on la connait a besoin d’eau pour exister.
