2. Cinématique du point

2.1 Vitesse et accélération \((\ast)\)

On considère le mouvement unidimensionnel décrit par : \(x(t) = x_0 e^{-\alpha t}\) pour \(t \geq 0\), où \(x_0\) et \(\alpha\) sont deux constantes positives.

1. Quelle est la dimension du paramètre \(x_0\) ? Du paramètre \(\alpha\) ?

2. Calculer la vitesse \(v(t)\). Vérifier la dimension du résultat.

3. Déterminer également l’accélération \(a(t)\).

4. Tracer la courbe représentative de la fonction \(x(t)\), sur laquelle on fera figurer le paramètre \(\alpha\).

Solution

Question 1.

Le paramètre \(x_0\) doit avoir la même dimension que \(x\), c’est-à-dire une longueur \(L\).

Comme vu en cours, l’argument de la fonction exponentielle doit être sans dimension, donc le paramètre \(\alpha\) doit être homogène à l’inverse d’un temps \(T^{-1}\).

Question 2.

La vitesse est donnée par la dérivée de la position en fonction du temps. On a ici une fonction composée:

\[\begin{split}\begin{align} f(u)=x_0 \cdot e^{u}\\ x(t)=-\alpha t \end{align}\end{split}\]

La dérivée d’une fonction composée d’obtient par: \(\frac{df(u)}{dt}=\frac{df}{du} \cdot \frac{du}{dt}\). Ici nous avons:

\[\begin{split}\begin{align} \frac{df}{du} &= x_0 \cdot e^{u} \\ \frac{dx}{dt} &= -\alpha \end{align}\end{split}\]

Donc finalement l’expression de la vitesse est:

\[\begin{split}\begin{align} \frac{dx(t)}{dt} &= x_0 \times e^{u} \times -\alpha\\ &= -\alpha x_0 e^{-\alpha t} \end{align}\end{split}\]

Vérifions la dimension du résultat obtenu:

\[\begin{split}\begin{align} [v]=[\alpha] \cdot [x_0]\\ [v]= T^{-1} \cdot L \end{align}\end{split}\]

On retrouve bien la dimension d’une vitesse.

Question 3.

L’expression de la vitesse est une fonction composée:

\[\begin{split}\begin{align} f(u)=-\alpha x_0 e^{u}\\ x(t)=-\alpha t \end{align}\end{split}\]

La dérivée d’une fonction composée d’obtient par: \(\frac{df(u)}{dt}=\frac{df}{du} \cdot \frac{du}{dt}\). Ici nous avons:

\[\begin{split}\begin{align} \frac{df}{du} &= -\alpha x_0 e^{u}\\ \frac{dx}{dt} &= -\alpha \end{align}\end{split}\]

Donc finalement l’expression de l’accélération est:

\[\begin{split}\begin{align} \frac{dv(t)}{dt} &= \overbrace{-\alpha x_0 e^{u}}^{\displaystyle{df / du}} \times \overbrace{-\alpha}^{\displaystyle{dx / dt}}\\ &= -\alpha^2 x_0 e^{-\alpha t} \end{align}\end{split}\]

Note: on vérifie facilement que la dimension de l’expression obtenue est bien \(L\cdot T^{-2}\).

Question 4.

Voici l’allure de la fonction pour \(x_0=10\) m et \(\alpha=5\) s.

(Source code, html)

2.2 Mouvement hélicoïdal \((\ast \ast)\)

On considère le mouvement d’un point M(x, y, z) décrit par les équations horaires :

\[\begin{split}\begin{align} x(t) &=\alpha \cos{\omega t} \\ y(t) &= \alpha \sin{\omega t} \\ z(t) &=\beta t \end{align}\end{split}\]

ou \(\alpha,\beta\) et \(\omega\) sont des constantes positives

1. Quelles sont les dimensions des paramètres α, β et ω ?

2. Déterminer les composantes du vecteur vitesse \(\vec{v}(t)\).

3. Procéder de même pour le vecteur accélération \(\vec{a}(t)\).

4. Montrer que la norme de ces deux vecteurs est constante. On rappelle que : cos² x + sin² x = 1.

5. Calculer le produit scalaire \(\vec{v} \cdot \vec{a}\). En déduire que \(\vec{v}\) et \(\vec{a}\) sont orthogonaux.

Solution

Question 1.

L’argument d’une fonction mathématique doit être sans dimension. Donc l’argument des fonctions sinus et cosinus \([\omega t]\) n’a pas de dimension. Or, comme \([t]=T\), il faut donc que \([\omega]=T^{-1}\) pour que \([\omega t]\) n’ait pas de dimension.

x, y et z dont des positions, et donc leur dimension est homogène à une longueur L. Comme les fonctions sinus et cosinus n’ont pas de dimension, on déduit que [α] est homogène à une longueur L. Pour que [β t] soit homogène à une longueur, il faut que \([\beta t] = [\beta] T = L\), et donc que \([\beta]= L T^{-1}\).

Question 2.

\[\begin{split}v_x(t) = \parder{x}{t} = \parder{(\alpha \cos{\omega t})}{t} = -\alpha \omega \sin{\omega t} \\ v_y(t) = \parder{y}{t} = \parder{(\alpha \sin{\omega t})}{t} = \alpha \omega \cos{\omega t} \\ v_z(t) = \parder{z}{t} = \parder{\beta t}{t} = \beta \\\end{split}\]

Question 3.

\[\begin{split}a_x(t) = \parder{v_x}{t} = \parder{(-\alpha \omega \sin{\omega t})}{t} = -\alpha \omega^2 \cos{\omega t} \\ a_y(t) = \parder{v_y}{t} = \parder{(\alpha \cos{\omega t})}{t} = -\alpha \omega^2 \sin{\omega t} \\ a_z(t) = \parder{v_z}{t} = \parder{\beta}{t} = 0 \\\end{split}\]

Question 4.

Par définition de la norme d’un vecteur, on a :

\[\begin{split}\begin{align} ||\vec{v}|| &= \sqrt{v_x^2 + v_y^2 + v_z^2} = \sqrt{\alpha^2 \omega^2 \sin^2{\omega t}+ \alpha^2 \omega^2 \cos^2{\omega t} + \beta^2} \\ &= \sqrt{\alpha^{2}\omega^{2} \underbrace{(\cos^2{\omega t} + \sin^2{\omega t} )}_{=1} + \beta^2} \\ &=\sqrt{\alpha^{2}\omega^{2} + \beta^2} \\ \end{align}\end{split}\]

\[\begin{split}\begin{align} ||\vec{a}|| &= \sqrt{a_x^2 + a_y^2 + a_z^2} = \alpha^2 \omega^4 \sin^2{\omega t}+ \alpha^2 \omega^4 \cos^2{\omega t} \\ &= \sqrt{\alpha^{2}\omega^{4} \underbrace{(\cos^2{\omega t} + \sin^2{\omega t} )}_{=1}} &=\sqrt{\alpha^{2}\omega^{4}} \\ &= \alpha \omega^2 \end{align}\end{split}\]

Question 5.

Le produit scalaire de deux vecteurs peut se calculer de deux façons. On a d’une part :

\[\begin{split}\begin{align} \vec{v}\cdot\vec{a} &= v_x a_x + v_y a_y + v_z a_z \\ &= (\alpha \omega \sin{\omega t} \times \alpha \omega^2 \cos{\omega t}) + (\alpha \omega \cos{\omega t} \times -\alpha \omega^2 \sin{\omega t}) + \beta \\ &= 0 \\ \end{align}\end{split}\]

D’autre part, on peut aussi écrire que le produit scalaire est égal à:

\[\vec{v} \cdot \vec{a}= ||\vec{v}|| \times ||\vec{a}|| \times \cos(\widehat{\vec{v},\vec{a}})\]

On sait que \(\vec{v}\neq 0\) et que \(\vec{a}\neq 0\), donc la seule possibilté pour que \(\vec{v} \cdot \vec{a}=0\) est que \(\cos(\widehat{\vec{v},\vec{a}})=0\). Pour que le cosinus d’un angle soit égal à zéro il faut que cet angle soit égal à \(\frac{\pi}{2}=90^{\circ}\), donc les 2 vecteurs doivent être perpendiculaires.

2.3 Nom de Zeus ! \((\ast \ast \ast)\)

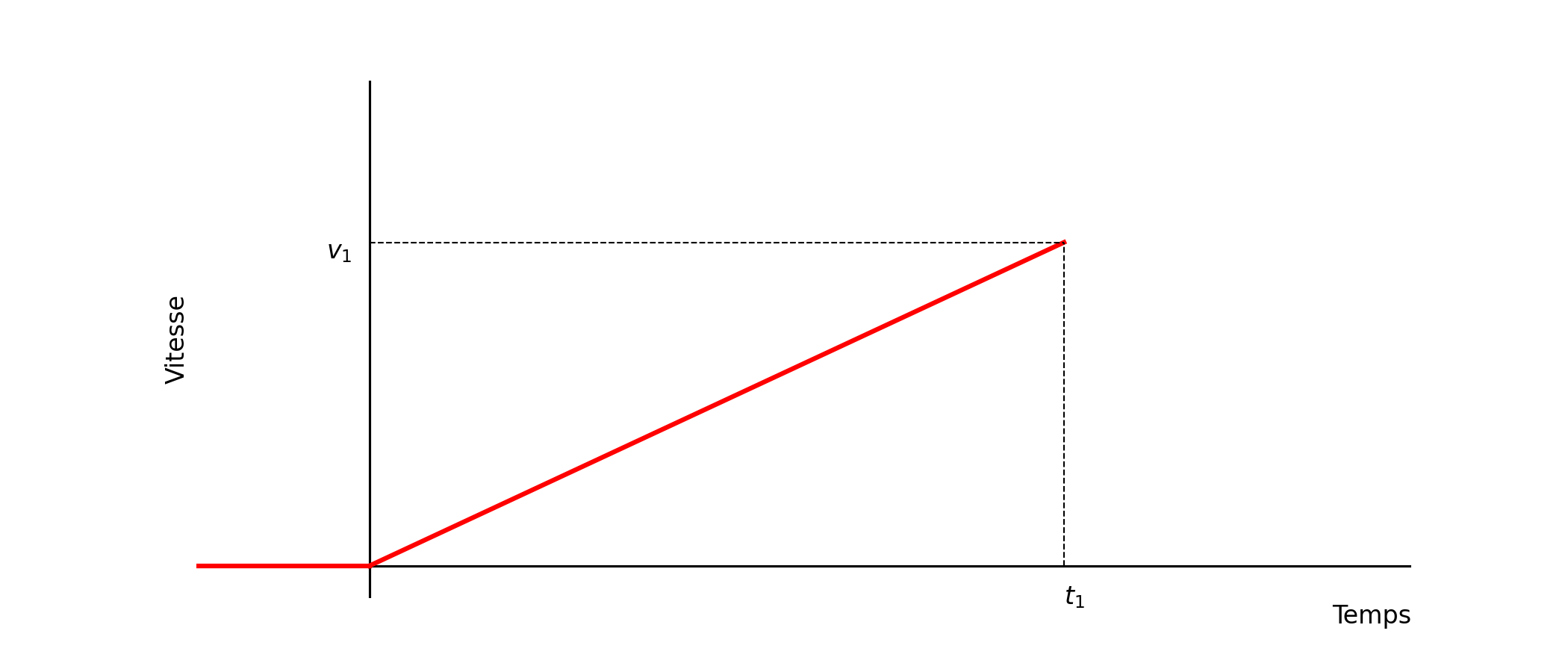
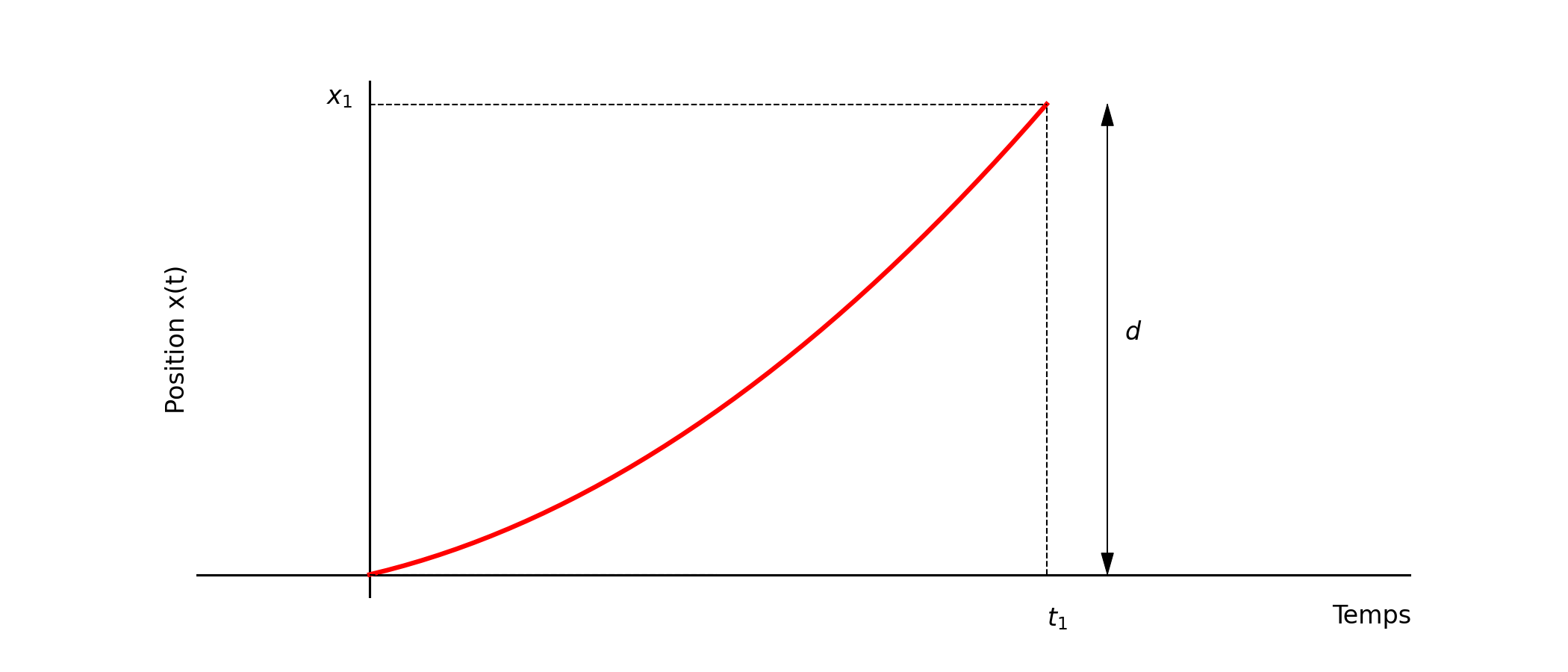
Dans le film « Retour vers le futur » de R. Zemeckis (1985), le héros Marty McFly doit atteindre au volant de sa DeLorean la vitesse \(v_0=88\) mph à l’instant précis où la foudre s’abat sur l’horloge de l’hôtel de ville. On note \(x(t)\) et \(v(t)\) respectivement la position et la vitesse du véhicule à l’instant \(t\), avec les conditions initiales \(x(0)=0\) et \(v(0)=0\). On suppose que le mouvement est rectiligne et uniformément accéléré : \(a(t)=a_0>0\). La distance qui sépare la position initiale de l’hôtel de ville est \(d=1~\text{mile} \ (\simeq 1609~\text{m})\).

1. Tracer graphiquement l’évolution de la vitesse, puis de la position, en fonction du temps.

2. Déterminer l’expression de \(v(t)\) pour \(t\geq 0\).

3. On note \(\tau\) l’instant où la voiture atteint la vitesse \(v_0\). Exprimer \(\tau\) en fonction de \(v_0\) et \(a_0\).

4. Déterminer également l’expression de \(x(t)\) pour \(t\geq 0\).

5. Étant donné que \(x(\tau)=d\), établir une relation entre \(a_0\), \(v_0\) et \(d\). En déduire que : \(\tau = 2d/v_0\)

6. La foudre frappe l’horloge précisément à 22h 04mn 00s. Déterminer, à la seconde près, l’heure à laquelle Marty doit démarrer.

Solution

Question 1.

Jusqu’à \(t=0\), la vitesse est nulle (la voiture n’a pas démarré). À partir de \(t\ge0\) la vitesse augmente de manière constante, on a donc une droite de pente \(a_0\).

Fig. 30 \(v(t)\)

Jusqu’à \(t=0\), la voiture est à sa position initiale en \(x=0\). À partir de \(t\ge0\) la vitesse augmente de manière constante et donc la position augmente de plus en plus rapidement.

Fig. 31 \(x(t)\)

Question 2.

Pour \(t\ge 0\) l’accélération est constante et donc: \(a(t=0)= a_0 = \frac{dv}{dt}\).

donc:

\(v(t)=a_0 t + C\).

Or, à l’instant \(t=0\) on a: \(v(t_0)=a_0 \times 0 + C = 0\) puisque la DeLorean démarre à l’arrêt. Donc: \(C=0\) et finalement:

\(\boxed{v(t)=a_0 t }\)

Question 3.

\[\begin{split}v(t=\tau)=v_0=a_0 \tau \\ \Leftrightarrow \boxed{\tau=\frac{v_0}{a_0}}\end{split}\]

Question 4.

La position s’obtient grâce à: \(v(t)=\frac{dx}{dt} \Rightarrow x(t) = \frac{a_0}{2} t^2 + C'\).

Or à l’instant \(t=0\) on a: \(x(t=0)=\frac{a_0}{2} \times 0^2 + C' = 0 \Rightarrow C'=0\)

et donc finalement: \(\boxed{x(t)=\frac{a_0}{2} t^2}\).

Question 5.

On a vu d’une part:

\[\begin{split}x(t)=\frac{a_0}{2} t^2 \\ \Rightarrow x(\tau)=\frac{a_0}{2} \tau^2 = d\end{split}\]

et d’autre part:

\[\tau=\frac{v_0}{a_0}\]

En injectant la seconde expression dans la première on obtient:

\[\begin{split}d= \frac{a_0}{2} \tau^2 = \frac{a_0}{2} \underbrace{\frac{v_0^2}{a_0^2}}_{\tau^2} \\ \Rightarrow \boxed{d = \frac{v_0^2}{2a_0}}\end{split}\]

On a donc:

(56)\[\begin{split}d=\frac{v_0^2}{2a_0} = \frac{v_0}{2} \times \underbrace{\frac{v_0}{a_0}}_{\tau} \\ \Leftrightarrow \boxed{\tau=\frac{2d}{v_0}}\end{split}\]

Question 6.

Étant donné que:

\[\begin{split}\begin{cases} d=1\text{ mile}=1609m\\ v_0=88mph=39.33 m\cdot s^{-1} \end{cases}\end{split}\]

on déduit immédiatement en utilisant la relation établie par l’équation (56) dans la question précédente que la durée \(\tau\) du trajet est:

\[\tau=\frac{2d}{v_0}=\frac{2\times1609}{39.33}=81.8s\]

Pour arriver précisément à 22h 04mn 00s, Marty doit donc démarrer à 22h 04mn 00s - 81.8s = 22h02min38s (en arrondissant à la seconde prêt)