5. La gravitation
Pour les applications numériques, on prendra : \(\mathcal{G} \simeq 6.67\times10^{-11}~\text{N} \cdot \text{m}^{2} \cdot \text{kg}^{-2}\).
5.1 Centrifugeuse (\(\ast\) - 5min)
Afin de préparer leurs missions, les astronautes s’entraînent à résister à des accélération extrêmes dans de grandes centrifugeuses, comme celle du centre de recherche de la NASA présentée sur la Fig. 9. La distance entre l’axe de rotation et le siège où s’installe l’astronaute est R= 18 m. Le système est mis en rotation à la vitesse angulaire ω = 20 tours/min. Étant donné la relation a = Rω², calculer l’accélération subie par l’astronaute. On exprimera le résultat en « nombre de g », où g ≃9, 8 m/s².
5.2 Gravité sur Mars (\(\ast\) - 5~10min)
On donne le rayon \(R_M\simeq 3\, 400\) km et la masse \(m_M\simeq 6,4 \times 10^{23}\) kg de la planète Mars.
Déterminer l’expression de l’accélération de la pesanteur \(g_M\) en fonction de \(m_M\), \(R_M\), et \(\mathcal{G}\).
Comparer le poids d’un astronaute de masse \(m=70\) kg sur Mars et sur la Terre.
5.3 Troisième loi de Kepler (\(\ast \ast\) - 20∼30min)
Une planète décrit une orbite circulaire autour d’une étoile de masse \(m\). On souhaite déterminer la relation entre la période \(T_p\) du mouvement et le rayon \(R_p\) de l’orbite. Pour cela, on procède par analyse dimensionnelle.
Quelle est l’unité de la constante gravitationnelle \(\mathcal{G}\) dans le système international ?
On suppose qu’il existe une relation de la forme : \(T_p=C\, R_p^{\alpha}\, m^{\beta}\, \mathcal{G}^{\gamma}\), où \(C\) est une constante numérique sans dimension. Déterminer la valeur des exposants \(\alpha\), \(\beta\) et \(\gamma\).
Vénus est la deuxième planète du système solaire. La période de son orbite est \(T_V\simeq 225\) jours. Étant donné la période (\(T_T\simeq 365\) jours) et le rayon (\(R_T\simeq 150 \times 10^6\) km) de l’orbite terrestre, calculer la rayon \(R_V\) de l’orbite de Vénus.
5.4 Orbite géostationnaire (\(\ast \ast\) - 10∼15min)
L’orbite géostationnaire est une orbite circulaire de période égale à la période de rotation de la Terre (\(T\simeq 24\) h). On donne : \(m_T \simeq 6 \times 10^{24}\) kg et \(R_T \simeq 6\, 400\) km.
Calculer l’altitude de l’orbite géostationnaire.
Déterminer la vitesse d’un satellite en orbite géostationnaire.
5.5 Points de Lagrange (\(\ast \ast \ast\) - 20∼30min)
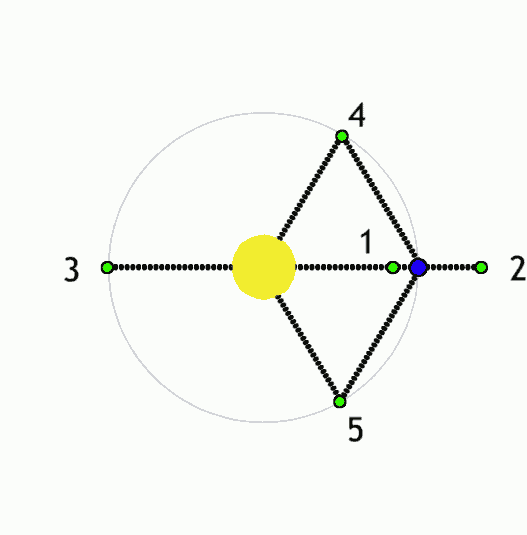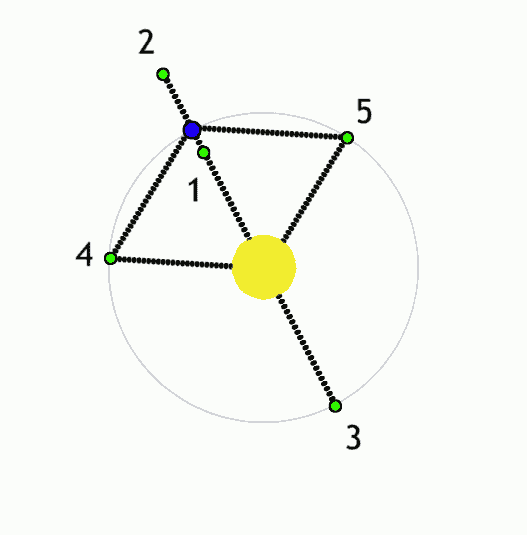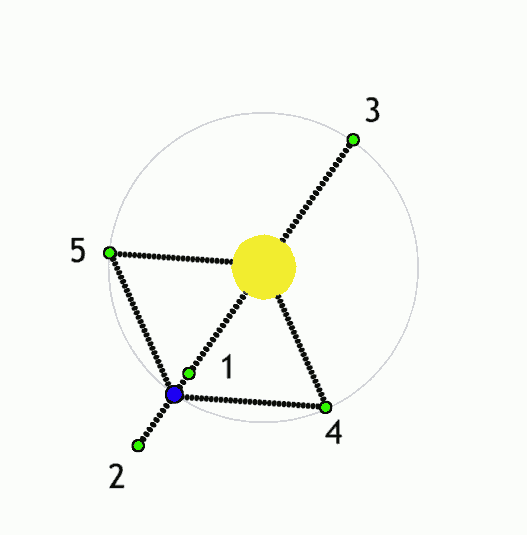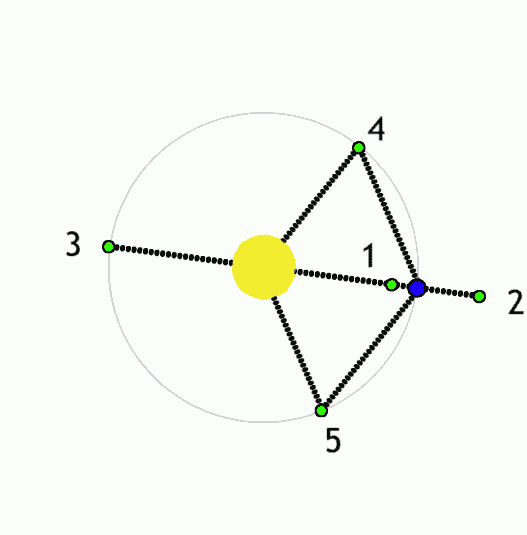
On considère un satellite de masse \(m\) situé sur l’axe Terre-Soleil — voir la Fig. 35. On souhaite déterminer les positions où les forces qui s’exercent sur le satellite se compensent. On note \(d\) la distance Terre-satellite et \(D\) la distance Terre-Soleil. On suppose que la masse \(m_T\) de la Terre est très inférieure à la masse \(m_S\) du Soleil. On néglige les forces d’inertie.
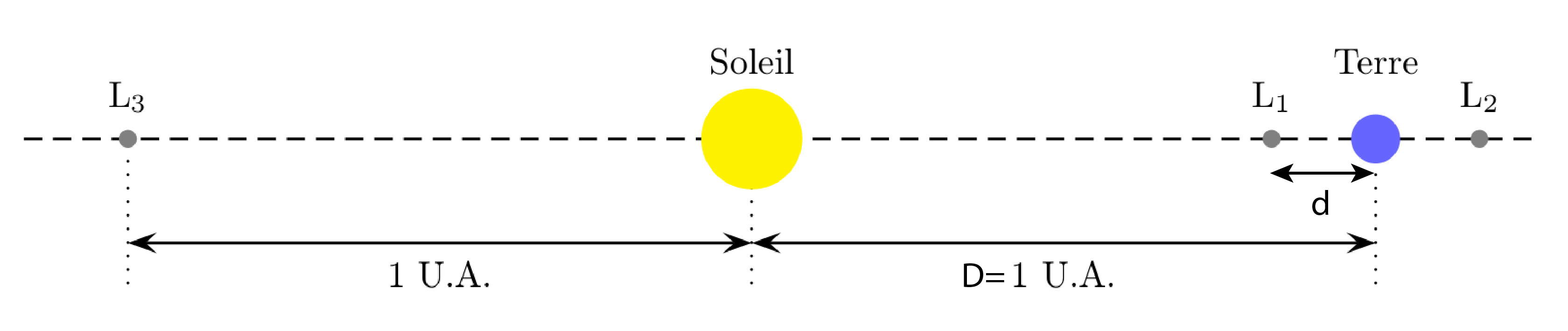
Fig. 35 Points de Lagrange sur l’axe Terre-Soleil.
On se place tout d’abord dans le cas où le satellite est situé au point \(\text{L}_1\) entre la Terre et le Soleil. Faire le bilan des forces et les représenter sur le schéma.
Montrer que la condition d’équilibre mécanique implique l’égalité : \(\frac{m_T}{d^2}=\frac{m_S}{\left( D-d\right)^2}\)
On suppose que \(d\ll D\). En déduire l’expression de la distance Terre-satellite \(d\) en fonction de \(m_T\), \(m_S\) et \(D\).
Faire l’application numérique pour \(m_T \simeq 6 \times 10^{24}\) kg, \(m_S\simeq 2 \times 10^{30}\) kg, et \(D\simeq 150 \times 10^6\) km. L’approximation \(d \ll D\) était-elle justifiée ?
L’équilibre mécanique est-il réalisable pour les points \(\text{L}_2\) et \(\text{L}_3\) ? Commenter.