A.3. Les lois du mouvement de Newton

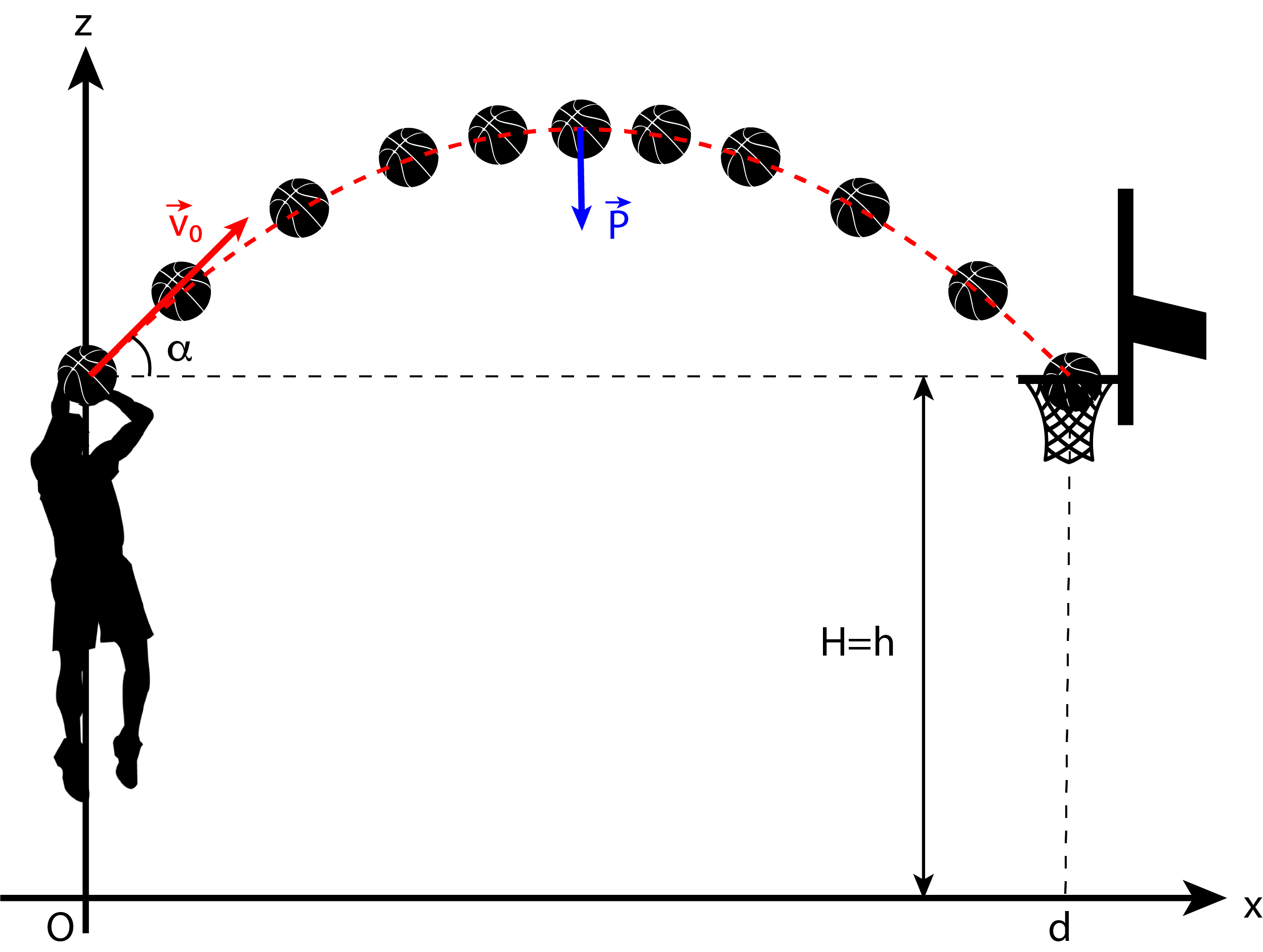
A.3.1) Lancé au basket-ball \((\ast \ast)\)

Au basket-ball, un panier est validé lorsque le ballon traverse l’arceau qui est situé à la hauteur \(H\). Le ballon est lancé de la hauteur \(h\) avec une vitesse initiale \(\vec{v}_0\) qui fait un angle \(\alpha\) avec l’horizontale. Le lanceur est situé à la distance horizontale \(d\) du panier. On assimile le ballon à un point matériel de masse \(m\). On suppose que la trajectoire est contenue dans le plan \(Oxz\), l’axe vertical \((Oz)\) étant orienté vers le haut. L’origine \(z=0\) correspond au niveau du sol.

Fig. 57 Lancé de basket-ball. Crédits: Toyota

1. Faire un schéma du problème. Donner les coordonnées des point définis dans l’énoncé.

2. Écrire les équations du mouvement. Préciser les conditions initiales.

3. En déduire les équations horaires \(x(t)\) et \(z(t)\).

4. Déterminer finalement l’équation de la trajectoire \(z(x)\).

On souhaite maintenant déterminer les paramètres du lancé pour que le panier soit réussi. On suppose que le joueur effectue son tir en extension, de telle sorte que : \(h=H\).

5. Donner la condition pour que le panier soit marqué.

6. Montrer que la problème admet une solution à condition que la vitesse \(v_0\) soit supérieure à une valeur seuil \(v_{0}^{\textrm{min}}\).

7. Déterminer cette vitesse seuil pour \(d=5\) m et \(g\approx 9,81~\text{m}\cdot \text{s}^{-2}\).

Rappels

On rappelle que : \(\sin 2 \alpha = 2 \sin \alpha \cos \alpha\).

Solution

Question 1.

Fig. 58 Lancé de basket-ball.

Le ballon est lancé à partir du point \(\begin{pmatrix}0\\ h\end{pmatrix}\).

Le panier est situé au point: \(\begin{pmatrix}d\\ H\end{pmatrix}\).

Le poids a pour coordonnées à tout instant \(\begin{pmatrix} 0 \\ -m g \end{pmatrix}\)

Question 2.

Le bilan des forces se résume au poids \(\vec{P}=m\vec{g}=-m g \vec{e}_{z}\).

Le principe fondamental de la dynamique va cond s’écrire: \(\sum \vec{F} = \vec{P} = m \vec{g} = m \vec{a} \Leftrightarrow \vec{a}=\vec{g}\).

Les conditions initiales au moment du lancé s’écrivent:

\[\begin{split}\begin{cases} \vec{r}(0)=\begin{pmatrix}0 \\ h\end{pmatrix} \\ \vec{v}(0)=\begin{pmatrix}v_0 \cos{\alpha}\\ v_0 \sin{\alpha} \end{pmatrix} \end{cases}\end{split}\]

Question 3.

Nous allons d’abord intégrer suivant l’axe \(Ox\):

\(a_{x}=\frac{dv_{x}}{dt}=0 \Rightarrow v_x(t)=C_1\)

or à l’instant \(t=0\) nous avons: \(v_x(0)=v_0 \cos{\alpha} = C_1\)

Donc finalement: \(\boxed{v_x(t)=v_0 \cos{\alpha}}\).

La vitesse suivant \(x\) est constante. Intuitivement c’est logique puisqu’aucune force horizontale ne s’applique sur le ballon une fois lancé.

On peut intégrer de nouveau pour déterminer l’expression de \(x(t)\):

\(v_x(t)=v_0 \cos{\alpha}=\frac{dx}{dt} \Rightarrow x(t)=v_0 t \cos{\alpha} + C_2\)

or à l’instant \(t=0\) nous avons: \(x(0)=0 = C_2\)

Donc finalement: \(\boxed{x(t)=v_0 t \cos{\alpha} }\).

Procédons de la même façon suivant \(Oz\):

\(a_z=\frac{dv_z}{dt}=-g \Rightarrow v_z(t)= -g t + C_3\)

Et à l’instant \(t=0\) nous avons: \(v_z(0)=v_0 \sin{\alpha} = C_3\)

Donc finalement: \(\boxed{v_z(t)= -g t + v_0 \sin{\alpha}}\).

On peut intégrer de nouveau pour déterminer l’expression de \(z(t)\):

\(v_z(t)=-g t v_0 \sin{\alpha}=\frac{dz}{dt} \Rightarrow z(t)=-\frac{1}{2} g t^2 + v_0 t \sin{\alpha} + C_3\)

À l’instant \(t=0\) nous avons: \(z(t)=h=C_3\).

Donc finalement: \(\boxed{z(t)=-\frac{1}{2} g t^2 + v_0 t \sin{\alpha} + h}\).

Question 4.

Exprimos \(t(x)\) pour ensuite reporter dans \(z(t)\):

\[\begin{split}x(t) &= v_0 t \cos{\alpha} \Leftrightarrow t = \frac{x}{v_0 \cos{\alpha}} \\ \Rightarrow z(x) &= -\frac{1}{2} g \Big(\frac{x}{v_0 \cos{\alpha}}\Big)^2 + v_0 \Big(\frac{x}{v_0 \cos{\alpha}}\Big) \sin{\alpha} + h \\\end{split}\]

(59)\[\boxed{z(x) = -\frac{g}{2v_0^2 \cos^2{\alpha}} x^2 + x \tan{\alpha} + h}\]

Question 5.

Pour que le panier soit marqué, il faut que \(z(d)=H\)

Question 6.

Fig. 59 Lancé de basket-ball. Le lanceur est en extension et lance le ballon depuis la hauteur \(h=H\).

Écrivons la condition \(z(d)=H\) avec \(h=H\) (Fig. 59). D’après l’équation (59):

\[\begin{split}z(d) = -\frac{g}{2 v_0^2 \cos^2{\alpha}} d^2 + d \tan{\alpha} + H &= H \\ \Leftrightarrow d\big(-\frac{g}{2v_0^2\cos^2{\alpha}} d + \frac{\sin{\alpha}}{\cos{\alpha}}\big) &= 0 \\ \Leftrightarrow d\big(d - \frac{2v_0^2 \cos\alpha \cos\alpha \sin{\alpha}}{g \cos{\alpha}}\big) &= 0 \\ \Leftrightarrow d\big(d - \frac{v_0^2\sin{2\alpha}}{g}\big) &=0\end{split}\]

Cette équation possède deux solutions:

\[\begin{split}\begin{cases} d=0 \\ d=\frac{v_0^2\sin{2\alpha}}{g} \end{cases}\end{split}\]

L’angle \(\alpha\) doit toujours être compris entre \(0\le \alpha\le \frac{\pi}{2}\), et donc \(0\le \sin{2\alpha} \le 1\). On voit alors que \(d \le \frac{v_0^2}{g}\), ou encore \(v_0^2\ge gd\). Pour qu’il y ait une solution et que le joueur marque un panier, il faut donc que la vitesse initiale remplisse la condition:

\(\boxed{v_0\ge\sqrt{gd}=v_{0}^{\rm min}}\).

Question 7.

Application numérique: \(v_0^{\rm min}=\sqrt{9.81\times5} = 7 m\cdot s^{-1}\).

A.3.2) Écran à tube cathodique \((\ast \ast \ast)\)

Dans les anciennes générations de télévisions, l’image est créée par un faisceau d’électrons qui vient frapper une surface recouverte d’une matière phosphorescente. La déflexion du faisceau est contrôlée par un champ électrique appliqué entre deux plaques métalliques parallèles à l’axe \((Ox)\). Le système est représenté sur la Fig. 60. Pour comprendre le principe de fonctionnement, on étudie le mouvement dans le plan horizontal \(Oxy\) d’un électron de masse \(m\) et de charge \(-e\). La région soumise au champ électrique \(\vec{E}=E \vec{e}_y\) correspond à l’intervalle \(0\leq x \leq L\). L’électron arrive de la gauche et pénètre au point \(O\) avec la vitesse initiale \(\vec{v}(0)=v_0 \vec{e}_x\).

1. Énumérer les forces qui sont mises en jeu. Laquelle peut-on négliger ?

2. En appliquant le principe fondamental de la dynamique, déterminer les équations horaires \(x(t)\) et \(y(t)\).

3. En déduire l’équation de la trajectoire \(y(x)\), ainsi que la valeur de l’ordonnée \(y_L=y(L)\) lorsque l’électron quitte la zone où règne le champ électrique.

4. Caractériser la trajectoire de l’électron dans la zone \(x>L\).

5. Un écran est placé en \(x=D\). Montrer que l’ordonnée \(y_D=y(D)\) à laquelle l’électron vient frapper l’écran peut se mettre sous la forme :

   \[y_D = k E\]

   où \(k\) est une constante que l’on déterminera en fonction des données du problème. Vérifier l’homogénéité du résultat.

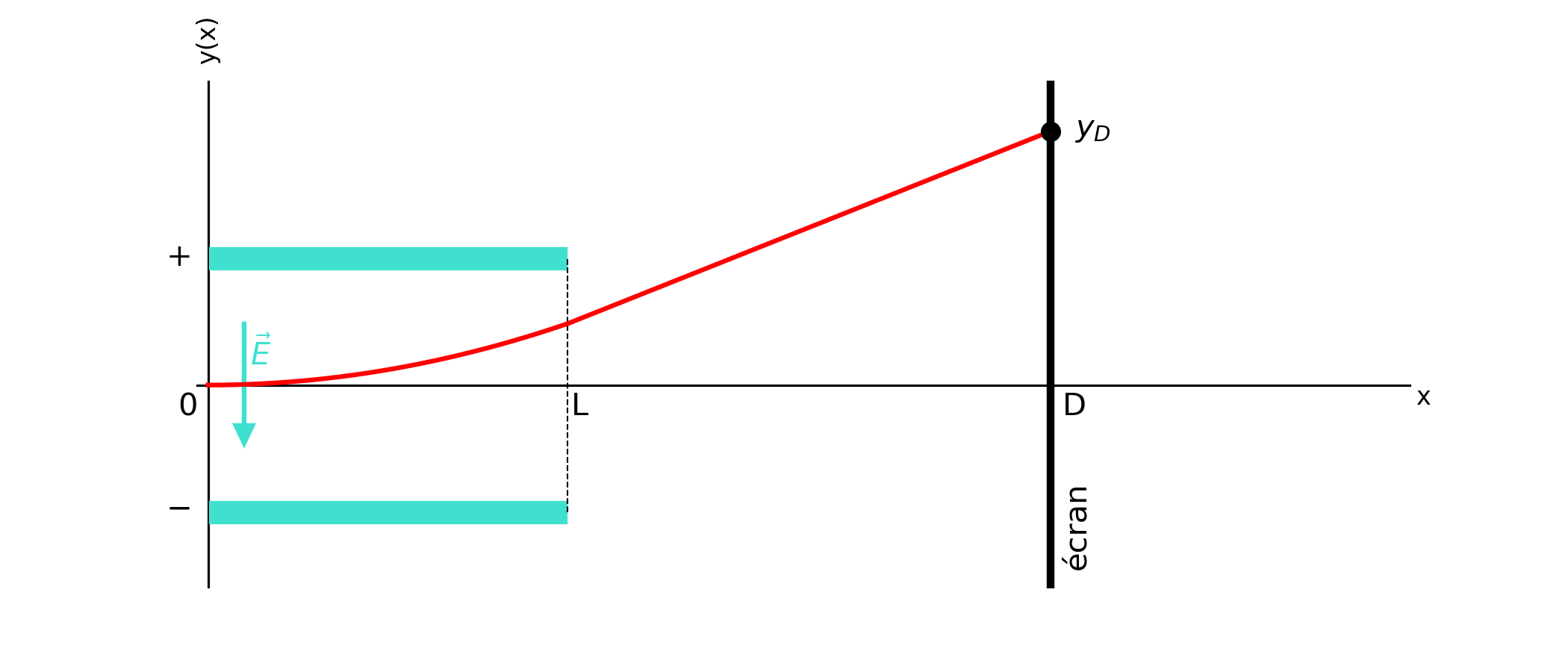
Fig. 60 Schéma du tube cathodique

Solution

Question 1.

Deux forces sont présentes: la poids et la force électrique:

\[\begin{split}\begin{cases} \vec{P}=m\vec{g} \Rightarrow \vert\vert \vec{P} \vert\vert = P = m g = 1.67 \times 10^{-27} \times 9.81 \approx 10^{-26} N \\ \vec{F}_c=-e \vec{E} \Rightarrow \vert\vert \vec{F_c} \vert\vert = F_c = 1.6\times10^{-19} \times 1 \approx 10^{-19} N \\ \end{cases}\end{split}\]

On voit que \(P<<F_c\) et donc qu’il peut être négligé.

Question 2.

Le principe fondamental de la dynamique s’écrit: (en négligeant le poids)

\[\begin{split}\sum \vec{F} = -e \vec{E} = m \vec{a} \Rightarrow \begin{cases}\frac{dv_x}{dt}= 0 \\ \frac{dv_y}{dt}=\frac{e}{m} E \end{cases}\end{split}\]

car \(\vec{E} = E \vec{e}_{y}\) est orienté suivant l’axe \(Oy\).

En intégrant on obtient:

\[\begin{split}\begin{cases} v_x(t)=C \\ v_y(t)=\frac{e}{m}E t + C' \end{cases}\end{split}\]

À \(t=0\) on a \(v_x(0)=v_0=C\) et \(v_{y}(0)=0 = C'\), et donc finalement:

\[\begin{split}\boxed{\begin{cases}v_x(t)=v_0 \\ v_{y}(t)=\frac{e}{m} E t\end{cases}}\end{split}\]

En intégrant une nouvelle fois, on obtient:

\[\begin{split}\begin{cases} x(t)=v_0 t + C_1 \\ y(t)=\frac{eE}{2m} t^2 + C_2 \end{cases}\end{split}\]

Les conditions initiales permettent de déduire:

\[\begin{split}\begin{cases} x(0)=C_1=0 \\ y(0)=C_2=0 \end{cases}\end{split}\]

et donc finalement:

\[\begin{split}\boxed{\begin{cases}x(t)=v_0 t \\ y(t)=\frac{eE}{2m} t^2 \end{cases}}\end{split}\]

Avertissement

Cette équation n’est valable qu’à l’intérieur du condensateur, c’est à dire en \(0\le x \le L\) !!!

Question 3.

L’équation horaire de \(x(t)\) permet d’écrire que: \(t=\frac{x}{v_0}\). En remplaçant \(t\) dans l’équation horaire de \(y(t)\) on obtient alors l’équation de la trajectoire:

\[\boxed{y(x) = \frac{e E}{2m v_0^2} x^2}\]

L’électron quitte donc le condensateur en \(\boxed{y(L)=\frac{e E}{2m v_0^2} L^2}\).

Question 4.

En \(x>L\), l’électron est isolé et ne subit plus aucune force extérieure. D’après le premier principe de la dynamique, il va donc suivre une trajectoire rectiligne uniforme, et conservera la vitesse (direction et amplitude) qu’il a acquise à la sortie du condensateur:

\[\begin{split} \begin{cases} v_x(t)=v_x(t_L=\frac{L}{v_0})=v_0 \\ v_y(t)=v_y(t_L=\frac{L}{v_0})=\frac{eE}{m}\frac{L}{v_0} \end{cases}\end{split}\]

On peut alors intégrer pour déterminer les nouvelles équations horaires. Commençons par \(x(t)\):

\(x(t)=v_0 t + C'_1\), avec \(x(t_L)=L=v_0 \frac{L}{v_0} + C'_1 \Rightarrow C'_1 = 0\)

et donc: \(\boxed{x(t)=v_0 t}\)

De même pour \(y(t)\):

\(y(t)=\frac{eE}{m}\frac{L}{v_0} t + C'_2\) avec \(y(t_L)=\frac{eE}{m}\frac{L^2}{v_0^2} + C'_2 = y_L = \frac{e E}{2m v_0^2} L^2 \Rightarrow C'_2 = -\frac{e E}{2m v_0^2} L^2 = -y_L\)

et donc finalement: \(\boxed{y(t)=\frac{eE}{m}\frac{L}{v_0} t - y_L}\).

Question 5.

L’électron atteind l’écran à l’instant \(t_D\) tel que:

\(x(t_D)=v_0 t_D = D\) et donc \(t_D=\frac{D}{v_0}\)

En reportant dans l’expression de \(y(t)\) on obtient:

\[\begin{split}y(t_D) &=\frac{eE}{m}\frac{L}{v_0} t_D - \frac{e E}{2m v_0^2} L^2 = \frac{eE}{m}\frac{L}{v_0} \frac{D}{v_0} - \frac{e E}{2m v_0^2} L^2 \\ &=\frac{eEL}{2mv_0^2}(2D-L)\end{split}\]

On trouve donc bien que:

\(y(t_D)=k \cdot E\) avec \(\boxed{k=\frac{eL}{2mv_0^2}(2D-L)}\)