3. Les lois du mouvement de Newton
Dans le chapitre précédent, nous avons étudié les propriétés des mouvements indépendamment de leur origine. Nous allons maintenant établir le lien entre les forces qui agissent sur un point matériel et le mouvement qui en résulte. Nous présentons d’abord les lois de Newton qui régissent les trajectoires des points matériels. Nous appliquons ensuite ces principes à la chute libre.
Mouvement d’un point matériel
Définitions
L’étude générale d’un mouvement est une question complexe : outre le déplacement de son centre de gravité, le système peut tourner sur lui-même ou encore se déformer. Le point de vue de la mécanique du point consiste à adopter la modélisation mathématique la plus simple possible en assimilant le système étudié à un point géométrique. On définit un point matériel \(M\) par :
son vecteur position \(\vec{r}=\overrightarrow{OM}\), dont découlent le vecteur vitesse \(\vec{v}= d \vec{r}/ d t\) ainsi que le vecteur accélération \(\vec{a}= d \vec{v} / d t\).
sa masse \(m\), dont l’unité est le kilogramme (kg).
En règle générale, on peut réduire un système à un point matériel si ses dimensions sont petites par rapport aux échelles caractéristiques du mouvement. Considérons par exemple le mouvement de révolution de la Terre autour du Soleil. Le rayon de la Terre est d’environ \(6,4\times 10^3\) km, alors que la distance Terre-Soleil vaut approximativement \(1,5\times 10^8\) km. Il est donc possible de réduire la Terre à un point matériel, de masse \(m_T\simeq 6\times 10^{24}\) kg.
Masse inerte
La masse \(m\) du point matériel qui intervient dans l’étude des mouvements est aussi appelée masse inerte. L’expérience montre en effet qu’il est plus difficile de communiquer une vitesse donnée à une balle de golf qu’à une balle de ping-pong. Il est aussi plus difficile de l’arrêter une fois qu’elle est lancée. On appelle inertie la résistance que présente un corps à toute modification de sa vitesse. Plus la masse du corps est importante, plus il aura tendance à conserver sa vitesse.
Forces élémentaires et forces de contact
Une force est une action physique ayant pour effet de produire ou modifier le mouvement d’un point matériel. Elle est spécifiée par un vecteur, généralement noté \(\vec{F}\). Une force est donc définie par sa direction, son sens et son intensité \(F=\Vert \vec{F} \Vert\). L’unité de force est le newton : \(1~\text{N}= 1~\text{kg}\cdot \text{m} \cdot \text{s}^{-2}\).
Au niveau fondamental, on ne connaît que 4 forces (ou interaction) élémentaires :
l’interaction gravitationnelle, qui gouverne l’attraction des corps sous l’effet de leur masse.
l’interaction électromagnétique, qui décrit les forces entre charges électriques.
l’interaction faible, qui est responsable de certaines désintégrations radioactives.
l’interaction forte, qui est impliquée dans le cohésion des noyaux atomiques.
Les interactions faibles et fortes sont toutes deux à très courte portée (au plus \(10^{-15}\) m) : elles sont donc pertinentes aux échelles subatomiques. L’interaction électromagnétique est dominante aux échelles microscopiques. Elle est impliquée dans la structure des atomes et des molécules. La force gravitationnelle prédomine quant à elle aux très grandes échelles. Elle gouverne la structure de l’univers.
L’expérience montre qu’il est néanmoins nécessaire d’introduire des forces supplémentaires pour décrire les phénomènes de la vie quotidienne. En effet, les interactions (d’origine électromagnétique) entre atomes et molécules se manifestent au niveau macroscopique par des forces de frottement (avec le fluide environnant ou entre solides) ou des forces de réaction (qui nous empêchent de passer à travers le sol par exemple). Bien que ces forces de contact dérivent des interactions fondamentales, elles ne sont pas considérées comme telles.
La force de pesanteur et la masse grave
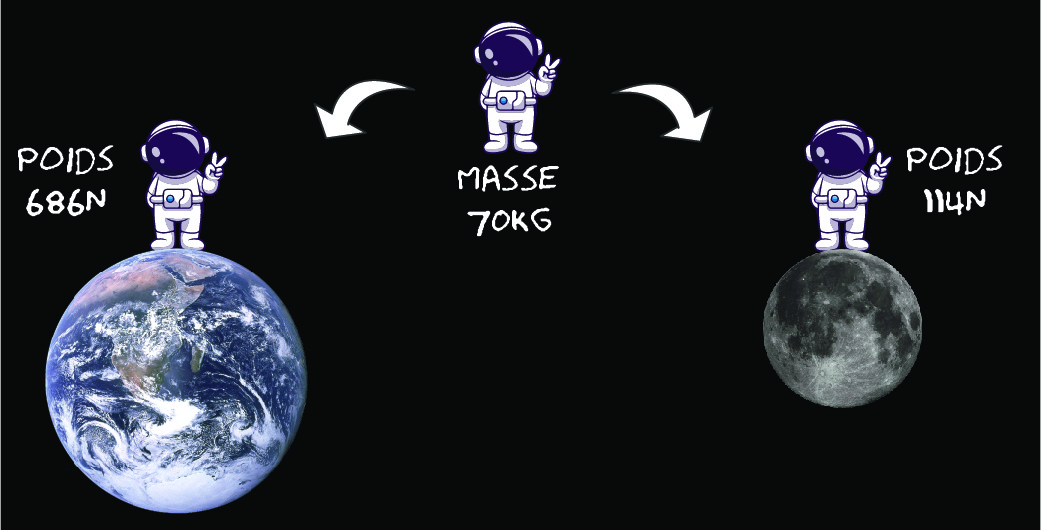
En pratique, les forces que nous allons étudier dans ce cours se divisent en deux catégories : les forces à distance (force de gravitation, force électromagnétique) et les forces de contact (forces de frottement, de réaction). Dans ce chapitre, nous serons encore plus restrictif en considérant uniquement la force de pesanteur. On définit le poids \(\vec{P}\):
(19)\[\vec{P} = m \vec{g} \ ,\]où le vecteur \(\vec{g}\) est l’accélération de la pesanteur, de direction verticale et orientée vers le bas, et \(m\) est la masse grave.
Attention!
Le poids étant une force, il se mesure en newton et non pas en kg ! Dans le langage courant, on assimile souvent le poids à la masse et on l’exprime de manière erronée en kilogrammes.
Dans le référentiel du quotidien qu’est la surface de la Terre, la force d’attraction exercée par la Terre est (plus ou moins) constante et par abus de langage, le mot «poids» est utilisé comme synonyme de la masse.
C’est un exemple important où le langage courant et le vocabulaire scientifique sont en conflit.
Alors que le poids d’un corps dépend des masses qui exercent une attraction sur ce corps (par exemple le poids change selon que l’on se trouve à la surface d’une planète plus ou moins massive), sa masse n’en dépend pas.
Fig. 10 Un astronaute de masse 70kg a un poids de 686N sur Terre et de 114N sur la Lune.
Nous verrons au Chapitre 5 que la force de pesanteur est une manifestation locale de l’interaction gravitationnelle. Elle dépend donc des propriétés du corps attracteur. À la surface de la Terre, l’intensité \(g = \Vert \vec{g} \Vert\) du champ de pesanteur vaut :
La masse grave
La masse grave (parfois appelée masse gravitationnelle ou masse pesante) est une mesure de la quantité de matière présente dans un objet.
Tous les objets macroscopiques qui nous entourent possèdent une masse gravitationnelle: les êtres vivants, les matériaux, les planètes, les galaxies, etc… À l’échelle des particules élémentaires, ce n’est pas le cas et certaines particules ne possèdent pas de masse gravitationnelle.
Dans le Système International, l’unité de la masse est le kilogramme (kg). Le Tableau 4 donnent les masses (ou l’ordre de grandeur) de quelques objets typiques allant des particules sub-atomiques au grandes structures de l’Univers.
Objet |
Masse (kg) |
|---|---|
Électron |
\(9\times10^{-31}\) |
Proton |
\(2\times10^{-27}\) |
Atome d’oxygène |
\(3\times10^{-26}\) |
Molécule d’insuline |
\(10^{-23}\) |
Amibe géante |
\(10^{-8}\) |
Fourmi |
\(10^{-5}\) |
Être humain |
\(10^{2}\) |
Baleine bleue |
\(10^{5}\) |
Terre |
\(6\times10^{24}\) |
Soleil |
\(2\times10^{30}\) |
Voix Lactée |
\(10^{41}\) |
Principe d’équivalence
Il n’y a a priori aucune raison fondamentale imposant que masse inerte et masse grave soient identiques, puisqu’elles sont définies de manière indépendante. C’est le principe d’équivalence énoncé par Einstein dans le cadre de la théorie de la relativité générale (1915) qui stipule que la masse inertielle et la masse gravitationnelle sont proportionnelles quel que soit le corps.
Avec un choix d’unités judicieux on donc peut facilement obtenir leur égalité, et on écrit souvent que le principe d’équivalence énonce l’égalité entre masse inertielle et masse gravitationnelle. Dans la suite de ce cours nous parlerons donc de masse, sans préciser s’il s’agit de la masse gravitationnelle ou inertielle.
Un peu d’Histoire…
Ce principe, comme tous les principes de la Physique, est un constat expérimental, jamais démenti mais inexpliqué. De nombreuses expériences ont testé cette égalité, réduisant toujours plus l’écart possible entre ces deux masses. La dernière en date a été menée e 2016 par le Centre National d’Études Spatiales avec le satellite MICROSCOPE et a demontré que la différence, si elle existe, doit être plus petite que \(2\times10^{-15}\).
Fig. 11 Le satellite MICROSCOPE (Crédit: CNES)
Les lois de la dynamique
En 1687, Issac Newton (1642-1727) formule un ensemble de trois lois fondamentales qui constituent encore aujourd’hui les bases de la mécanique classique. Ses travaux marquent un tournant décisif dans l’histoire des sciences en proposant une description mathématique de la physique.
Première loi de Newton
En mécanique du point, un système est dit isolé s’il n’est soumis à aucune force extérieure [1]. En pratique, cette définition a peu de sens car il est difficile — voire impossible — de soustraire un système de toute influence externe. On introduit alors la notion de système pseudo-isolé lorsque la résultante des forces qui lui sont appliquées est nulle. La première loi de Newton, ou principe d’inertie, s’énonce de la manière suivante :
1.1 Principe d’inertie
Il existe une famille de référentiels, appelés référentiels galiléens, tels que, par rapport à l’un de ces référentiels, tout système isolé ou pseudo-isolé est soit au repos, soit animé d’un mouvement rectiligne uniforme.
où \(\vec{v}_0\) est un vecteur constant (\(\vec{v}_0 = \vec{0}\) pour un système au repos).
Le principe d’inertie fait appel à la notion de référentiel, que l’on définit comme un ensemble de points fixes par rapport auxquels on repère une position ou un mouvement. Considérons par exemple un train qui se déplace selon un mouvement rectiligne uniforme. Le principe d’inertie s’applique aussi bien pour un observateur à l’intérieur du train (qui est lié au référentiel en translation uniforme) que pour un observateur extérieur (qui est lié au référentiel fixe de la gare par exemple). Par contre, si le train freine ou suit une trajectoire courbe, l’observateur à l’intérieur du train ressent des forces d’inertie. Dans ce cas, la première loi de Newton ne s’applique plus.
Le principe d’inertie inclut donc une définition empirique d’un référentiel galiléen. Cependant, le caractère inertiel d’un référentiel reste toujours approximatif. Par exemple, le référentiel terrestre n’est pas parfaitement galiléen car la Terre tourne sur elle-même. En pratique, nous n’aborderons ce semestre que des situations où le principe d’inertie est vérifié. Il sera donc toujours sous-entendu que le référentiel d’étude est galiléen.
Parmi les référentiels galiléens que nous rencontrerons, on peut citer :
le référentiel de Copernic (ou héliocentrique), qui a pour origine le centre du Soleil et dont les axes sont définis par trois étoiles suffisamment éloignées pour pouvoir être considérées comme fixes. Il permet d’étudier le mouvement des planètes.
le référentiel géocentrique, qui a pour origine le centre de masse de la Terre et dont les axes sont parallèles à ceux du référentiel de Copernic. Il sert, par exemple, à l’étude du mouvement des satellites artificiels.
le référentiel terrestre, qui a pour origine un point de la Terre et dont les axes ont des directions fixes (par exemple : le repère défini par trois arêtes d’une salle de classe).
Le caractère inertiel d’un référentiel reste toujours approximatif. En effet, la Terre tournant sur elle-même, le référentiel terrestre n’est pas parfaitement galiléen. De la même façon, la Terre tourne autour du Soleil, ce dernier tournant autour du centre de la Voie Lactée. Il en résulte que ni le référentiel géocentrique, ni le référentiel héliocentrique ne sont parfaitement galiléens.
Deuxième loi de Newton
La deuxième loi de Newton, ou principe fondamental de la dynamique, s’énonce ainsi :
1.2 Principe fondamental de la dynamique.
Dans un référentiel galiléen, la somme des forces extérieures appliquées au système est égale au produit de sa masse et de son accélération.
Il est intéressant de noter que l’on retrouve le principe d’inertie dans le cas d’un système isolé :
où \(\vec{v}_0\) est un vecteur constant. Pour autant, le principe d’inertie (20) ne doit pas être considéré comme un cas particulier de l’équation (22). En effet, le principe d’inertie est un préalable permettant d’identifier, de manière opérationnelle, les référentiels galiléens dans lesquels le principe fondamental de la dynamique peut ensuite être appliqué. Précisons également que, si le principe d’inertie énonce qu’aucune force extérieure n’est requise pour entretenir un mouvement rectiligne uniforme, l’action de forces extérieures est nécessaire pour modifier le vecteur vitesse (en norme et en direction).
Troisième loi de Newton
La troisième loi de Newton est également appelée principe des actions réciproques :
1.3 Principe des actions réciproques.
Si un corps \(A\) exerce une force sur un corps \(B\) , il subit en retour une force d’intensité égale, de même direction mais de sens opposé.
Fig. 12 Action et réaction.
Ce principe implique en particulier que les deux forces sont portées par la droite qui relie les points \(A\) et \(B\) — voir la Fig. 12 ci-contre. Newton a fait appel à ce principe pour déterminer l’expression de la force de gravitation entre deux corps massifs, qui sera discutée au Chapitre 5. En pratique, cette loi est surtout invoquée lorsque l’on étudie une assemblée de points matériels en interaction.
Application à la chute libre
Présentation de la méthodologie
Afin d’illustrer les lois de Newton, nous considérons le mouvement d’un point matériel soumis uniquement à son poids \(\vec{P}=m\vec{g}\). Cet exemple nous permet de présenter la démarche qui sera suivie de façon systématique pour l’étude des mouvements en mécanique.
Résolution d’un problème de mécanique du point
Définition du système : quel est le système étudié ? Cette question est importante quand on étudie plusieurs points matériels en interaction (système planète-satellite par exemple).
Bilan des forces : cette étape essentielle consiste à recenser l’ensemble des forces qui s’appliquent au système, quitte éventuellement à en négliger certaines par la suite.
Définition du repère et schéma : on représente le système à un instant quelconque. Le schéma constitue une aide précieuse au moment de projeter les forces sur les axes du repère.
Principe fondamental de la dynamique : on écrit d’abord l’égalité vectorielle, que l’on projette ensuite pour obtenir les équations du mouvement.
Résolution des équations du mouvement : on remonte à la vitesse puis à la position en fonction du temps, en tenant compte des conditions initiales.
Au final, ce raisonnement permet d’obtenir les équations horaires du mouvement, c’est-à-dire les fonctions \(x(t)\), \(y(t)\) et \(z(t)\). On peut ensuite en déduire toutes les quantités physiques pertinentes (énergie, fréquence d’un mouvement périodique, …).
Mouvement de chute libre
Appliquons la méthodologie au mouvement de chute libre d’un point matériel :
Système : le point matériel de masse \(m\).
Bilan des forces :
poids \(\vec{P}=m\vec{g}\)
les autres forces éventuelles (frottements de l’air par exemple) sont négligées
Repère : on considère le repère cartésien \(Oxyz\), l’axe vertical \((Oz)\) étant orienté vers le haut, représenté sur la figure 1.1(a).
Principe fondamental de la dynamique : \(\vec{P} = m\vec{a}\)
On voit donc que la masse disparaît de l’équation du mouvement :
Nous pouvons directement conclure que le mouvement de chute libre d’un point matériel est indépendant de sa masse. Ce résultat contre-intuitif n’est valable que dans le vide. Dans un fluide, il faudrait tenir compte des forces de frottement (cf. Chapitre 4).
Le principe fondamental permet donc de déterminer l’accélération du point matériel. Nous exprimons maintenant la vitesse puis la position en fonction du temps, selon que la vitesse initiale soit nulle ou non.
Chute libre sans vitesse initiale
Nous supposons tout d’abord que la particule est lâchée à l’instant \(t=0\) de l’altitude \(h\), sans vitesse initiale. Les conditions initiales correspondantes sont donc :
Dans ce cas, le mouvement est entièrement vertical : \(x(t)=y(t)=0\). On projette alors l’égalité vectorielle (23) sur l’axe \((Oz)\) :
où nous avons tenu compte de : \(\vec{g}=(0,0,-g)\). En intégrant cette équation, on obtient :
où la constante d’intégration \(C\) est fixée grâce à la condition initiale (24). On peut donc écrire :
On obtient finalement l’expression de la vitesse en fonction du temps :
Nous pouvons ensuite déterminer la position en intégrant cette dernière relation :
La constante d’intégration \(C\,'\) s’obtient en tenant compte de l’autre condition initiale (24):
Finalement, l’évolution de la position en fonction du temps est donnée par la formule :
Ce résultat constitue ce qu’on appelle l’équation horaire du mouvement.
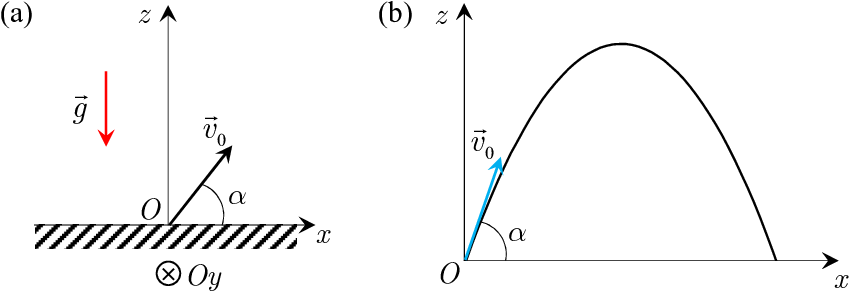
Fig. 13 Gauche (a) Mouvement balistique d’un point matériel dans le champ de pesanteur uniforme. Droite (b) Trajectoire parabolique du point matériel [Équation (39)].
Mouvement balistique
Nous considérons maintenant la situation plus générale où le point matériel est lancé avec une vitesse initiale non nulle, comme illustré sur la figure 1.1(a). Étant donné la définition \(\vec{a}= d \vec{v} / dt\), l’équation du mouvement (23) peut encore s’écrire :
Conditions initiales
Position : on définit le repère \(Oxyz\) de telle sorte que l’origine \(O\) coïncide avec la position du point matériel à l’instant initial \(t=0\) :
(31)\[\vec{r}(0)=\vec{0} \quad \Rightarrow \quad x(0)= 0 \ , \quad y(0)=0 \ , \quad \text{et} \quad z(0)= 0 \ .\]Vitesse : à l’instant initial, le vecteur vitesse de norme \(v_0\) fait un angle \(\alpha\) avec l’horizontale :
(32)\[\vec{v}(0)=\vec{v}_0 \quad \Rightarrow \quad v_x(0)= v_0 \cos \alpha \ , \quad v_y(0)=0 \ , \quad \text{et} \quad v_z(0)= v_0 \sin \alpha \ .\]
Composantes de la vitesse
L’équation (30) étant une égalité entre vecteurs, la première étape consiste à projeter cette équation selon les trois directions de l’espace. On obtient alors trois équations :
Chacune de ces équations s’intègre aisément :
où \(A\), \(B\) et \(C\) sont des constantes d’intégrations. Pour les déterminer, nous comparons les expressions (34) évaluées à \(t=0\) avec les conditions initiales (32). On obtient : \(A=v_0 \cos \alpha\), \(B=0\), et \(C=v_0 \sin \alpha\). Les composantes de la vitesse sont finalement données par :
Équations horaires du mouvement
Afin d’obtenir les équations horaires, on fait appel à la définition de la vitesse que l’on projette sur les 3 directions de l’espace :
En utilisant les expressions de l’équation (35), nous obtenons alors :
Les constantes d’intégration sont déterminées encore une fois grâce aux conditions initiales (31) : \(x(0)=y(0)=z(0)=0 \ \Rightarrow \ A'=B\,'=C\,'=0\). Finalement, les équations horaires s’écrivent :
Les équations horaires montrent que le mouvement s’effectue dans le plan défini par les vecteurs \(\vec{v}_0\) et \(\vec{g}\). Il correspond à la combinaison de deux mouvements rectilignes :
dans la direction \((Ox)\), la composante de la force est nulle et le mouvement est rectiligne uniforme, comme le requiert le principe d’inertie.
dans la direction \((Oz)\), on retrouve le mouvement uniformément accéléré que nous avions discuté au paragraphe 1.3.3.
Équation de la trajectoire
Enfin, on peut noter que l’équation de la trajectoire \(z(x)\) s’obtient en éliminant le paramètre \(t\) entre les expressions de \(x(t)\) et de \(z(t)\) dans l’équation (38) :
La trajectoire est donc une parabole, représentée sur la Fig. 13 (b).
Testez vos connaissances
Après avoir étudier ce chapitre, testez vos connaissances sur Wooclap
