A.2. Cinématique du point

A.2.1 Dérivées et primitives \((\ast)\)

1. Calculer les dérivées des fonctions suivantes :

   \[f_1(t)=\cos 2t \ , \quad f_2(t)=\frac{1}{t+1} \ , \quad f_3(t) = e^{-3t} , \quad \text{et} \quad f_4(t) = e^{t^2} \ .\]

2. Déterminer les primitives des fonctions suivantes :

   \[g_1(t)=\frac{\pi}{2} \ , \quad g_2(t)=t+1 \ , \quad g_3(t)=\frac{1}{t^2} \ , \quad \text{et} \quad g_4(t) = e^{2t} \ .\]

Solution

Question 1.

\[\begin{split}f_1(t) = \cos{2t} &\Rightarrow \frac{df_{1}}{dt} = -2\sin{2t} \\ f_2(t) = \frac{1}{+1} &\Rightarrow \frac{df_{2}}{dt} = -\frac{1}{(t+1)^2} \\ f_3(t) = e^{-3t} &\Rightarrow \frac{df_{3}}{dt} = -3 e^{-3t} \\ f_4(t) = e^{t^2} &\Rightarrow \frac{df_{1}}{dt} = 2t e^{t^2}\\\end{split}\]

Question 2.

\[\begin{split}g_1(t) = \frac{\pi}{2} &\Rightarrow G_1{t} = \frac{\pi}{2} t + C_1 \\ g_2(t) = t+1 &\Rightarrow G_2{t} = \frac{t^2}{2} + t + C_2 \\ g_3(t) = \frac{1}{t^2} &\Rightarrow G_3{t} = -\frac{1}{t} + C_3 \\ g_4(t) = e^{2t} &\Rightarrow G_4{t} = \frac{1}{2} e^{2t} + C_4 \\\end{split}\]

A.2.2 conduite en ville \((\ast)\)

Une voiture roule en ligne droite. L’évolution de sa vitesse en fonction du temps est représentée sur le graphique de la Fig. 46 ci-dessous. Indiquer les instants pour lesquels:

1. La voiture est immobile

2. La voiture est animée d’un mouvement uniforme

3. l’accélération de la voiture est constante

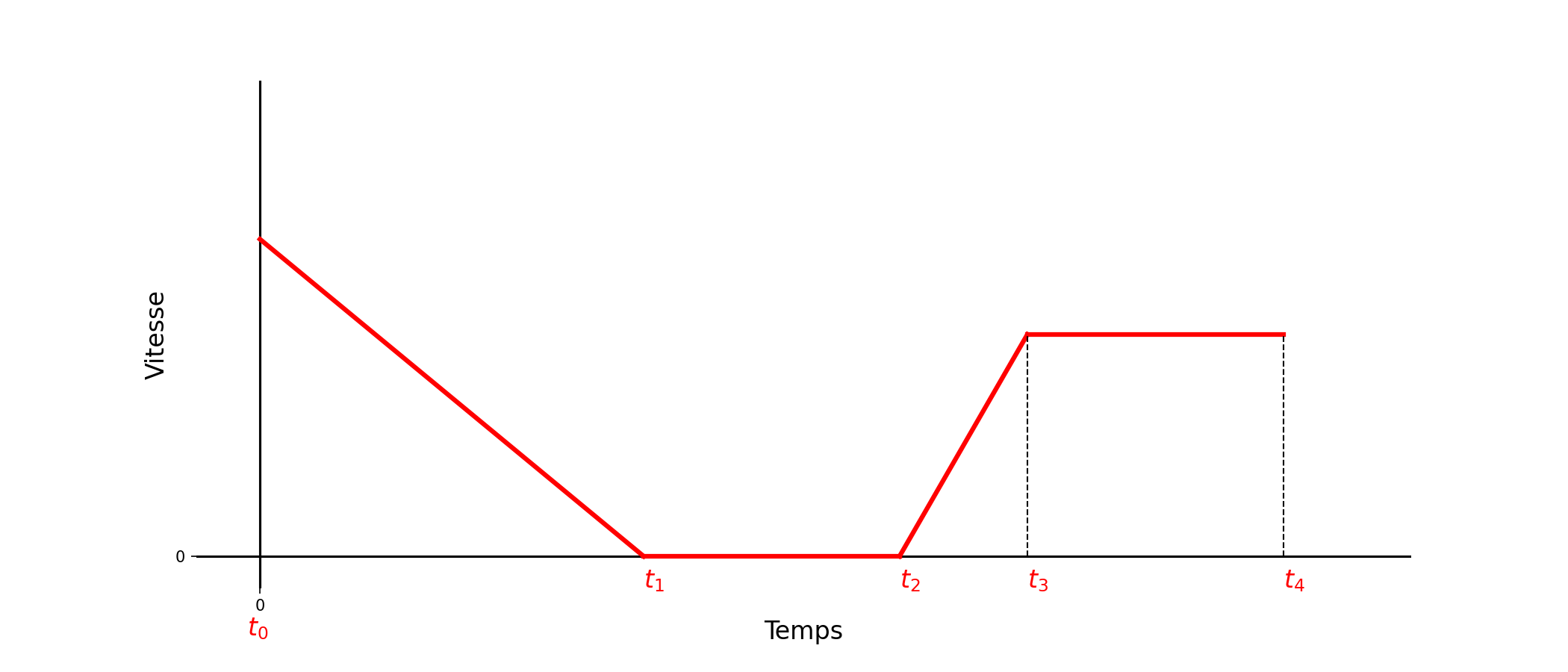
Fig. 46 Vitesse de la voiture en fonction du temps.

Solution

Question 1.

La voiture est immobile quand la vitesse est nulle, donc entre \(t_1\) et \(t_2\).

Question 2.

La voiture est animée d’un mouvement uniforme, c’est à dire qu’elle se déplace à une vitesse constante, entre les instants \(t_3\) et \(t_4\).

Question 3.

La voiture subit une accélération constante lorsque la vitesse varie de manière linéaire, donc entre les instant \(t_0\) et \(t_1\), puis entre les instants \(t_2\) et \(t_3\).

A.2.3 Distance de freinage \((\ast \ast)\)

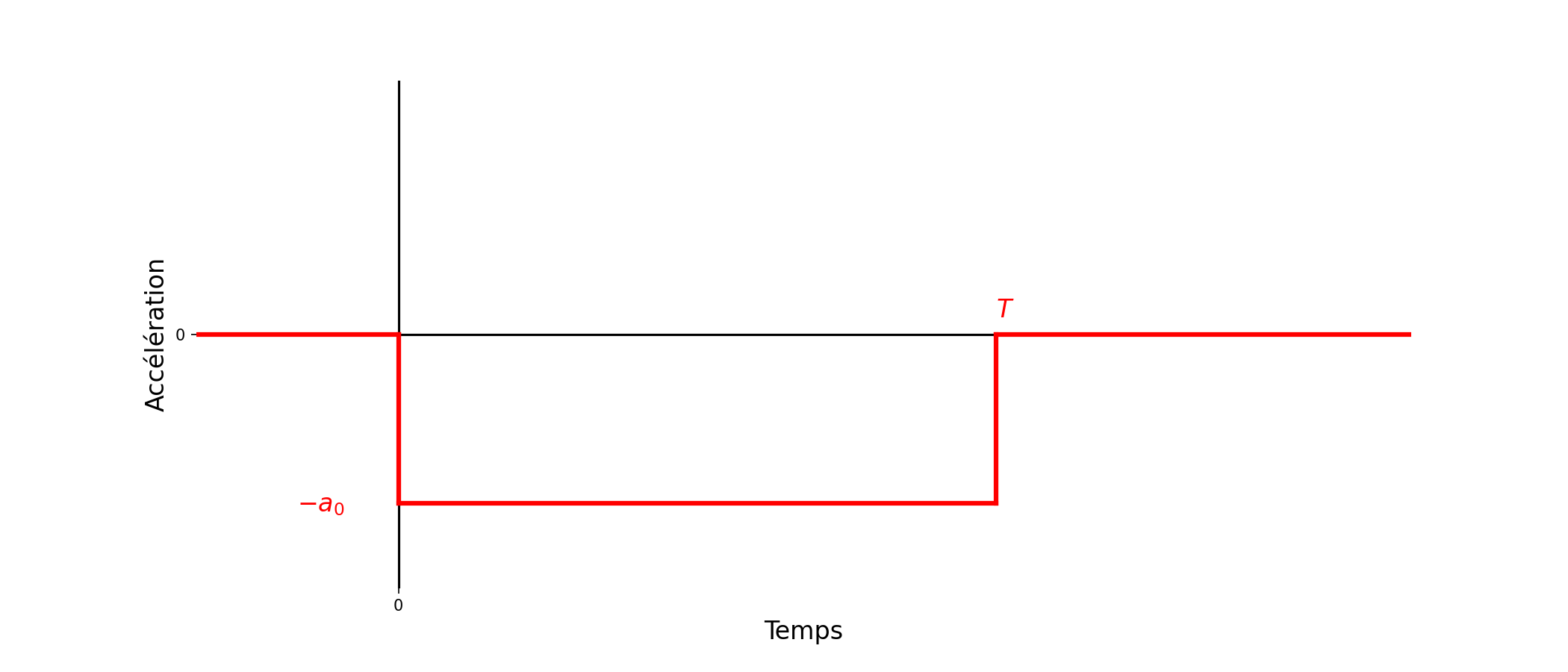
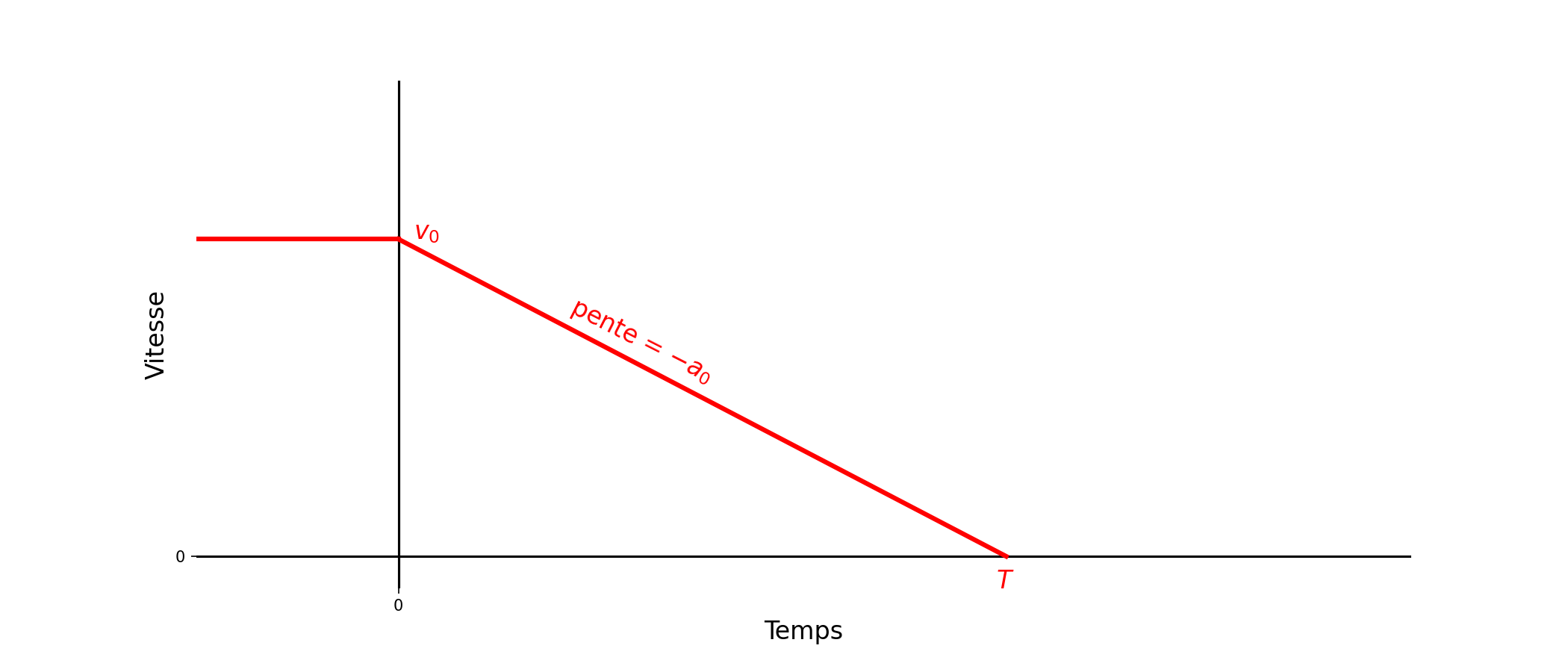
On considère un train qui se déplace en ligne droite. Initialement, sa vitesse est \(v_x(t)=v_0\). À l’instant \(t=0\), le conducteur déclenche le freinage d’urgence. Le train subit alors une « décélération » constante \(a_x(t)=-a_0\) (avec \(a_0>0\)).

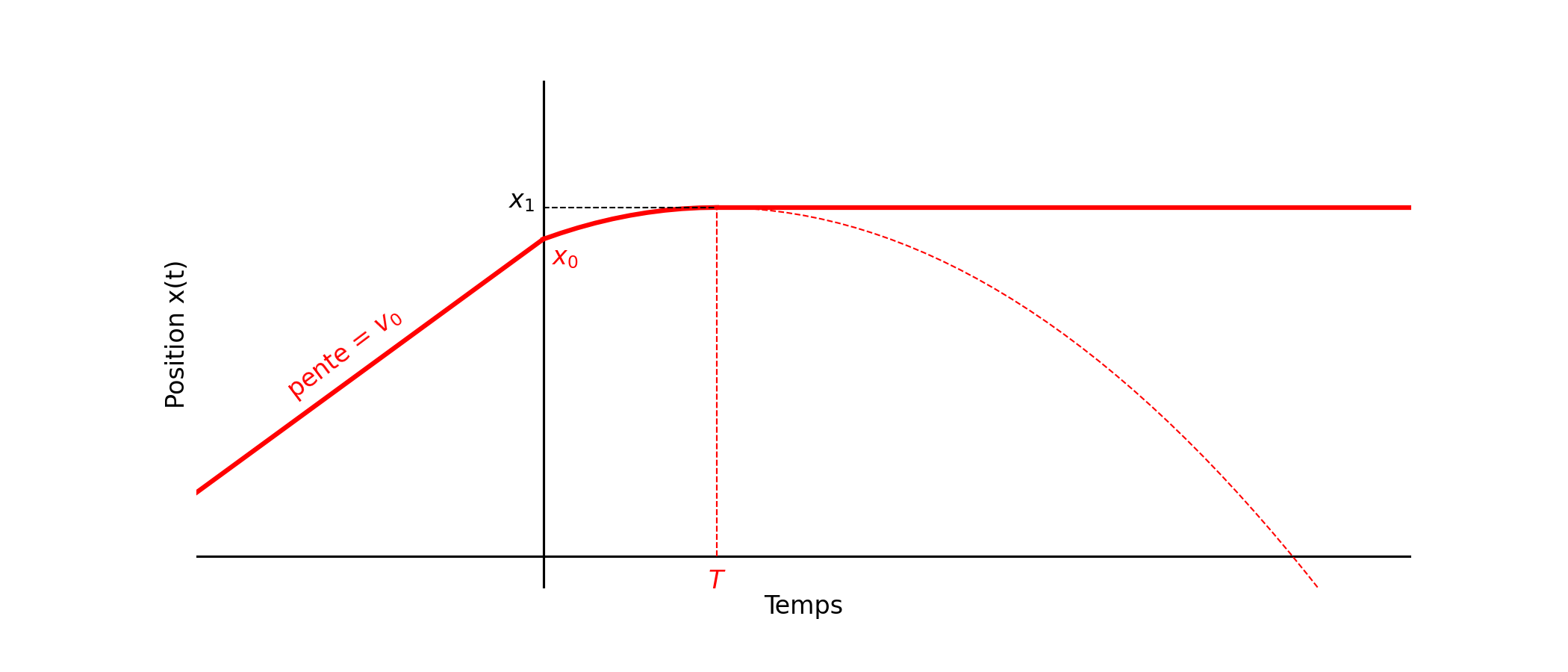
1. Tracer graphiquement l’évolution de \(a_x(t)\), puis de \(v_x(t)\) et de \(x(t)\).

2. Déterminer l’expression de \(v_x(t)\) pour \(t>0\). Au bout de combien de temps le train s’arrête-t-il ?

3. Calculer la distance \(L\) parcourue par le train entre le moment où il commence à freiner et son arrêt complet.

Application numérique : évaluer \(L\) pour \(v_0=300\) km/h et \(a_0=1,2~\text{m}\cdot\text{s}^{-2}\).

Solution

Question 1.

Fig. 47 \(a_x(t)\): lorsque \(t<0\), alors \(v_{x}(t)=v_0\) et donc \(a_{x}(t)=0\).

Fig. 48 \(v_x(t)\): lorsque \(t<0\), alors \(v_{x}(t)=v_0\). Après \(t\ge0\) la vitesse diminue de façon linéaire avec une pente égale à \(-a_0\).

Fig. 49 \(x(t)\): lorsque \(t<0\), alors la position augmente de façon linéaire avec une pente \(v_0\). Après \(t\ge0\), la position continue d’augmenter mais en suivant une courbe parabolique, jusqu’à l’instant \(T\) où le train s’arrête et la position ne change plus.

Question 2.

Pour \(t<0\), on a \(v_{x}(t)=v_0 \Rightarrow a_{x}(t)=\frac{dv_{x}}{dt}=0\)

Pour \(t\ge0\), on a \(a_{x}(t)=-a_0=\frac{dv_{x}}{dt}\)

Donc: \(v_{x}(t)=-a_{0} t + C\) où \(C\) est une constante que l’on peut déterminer en regardant ce qui se passe à l’instant \(t=0\) où l’on connait tous les paramètres:

\(v(t=0)=v_0=-a_{0} \times 0 + C = C \Rightarrow C=v_0\)

et donc finalement:

\(\boxed{v_{x}(t)=-a_0 t + v_0}\)

Le train s’arrête quand \(v(t=T)=-a_0 T + v_0 = 0\), et donc: \(\boxed{T=\frac{v_0}{a_0}}\)

Question 3.

Pour cela, on va exprimer la position \(x(t)\). Par définition \(v_{x}(t)=\frac{dx}{dt}\), donc:

\(x(t)=-\frac{a_0}{2} t^2 + v_0 t + C'\) où \(C'\) est une constante que l’on va déterminer en regardant les conditions initiales.

On a \(x(t=0)=-\frac{a^2}{2} \times 0^2 + v_0 \times 0 + C' = x_0 \Rightarrow C'= x_0\)

Et donc: \(\boxed{x(t)=-\frac{a_0}{2} t^2 + v_0 t + x_0}\).

La distance parcourue est alors simplement obtenue par: \(L=x(T)-x(0)\) avec d’après ce qui précède \(T=\frac{v_0}{a_0}\). Soit:

\(L=\underbrace{-\frac{a_0}{2} \Big(\frac{v_0}{a_0} \Big)^2 + v_0 \frac{v_0}{a_0} + x_0}_{x(T)} - \underbrace{x_0}_{x(0)}\)

et donc:

\(\boxed{L=\frac{v_0^2}{2a_0}}\)

Application numérique: L=2893.5m

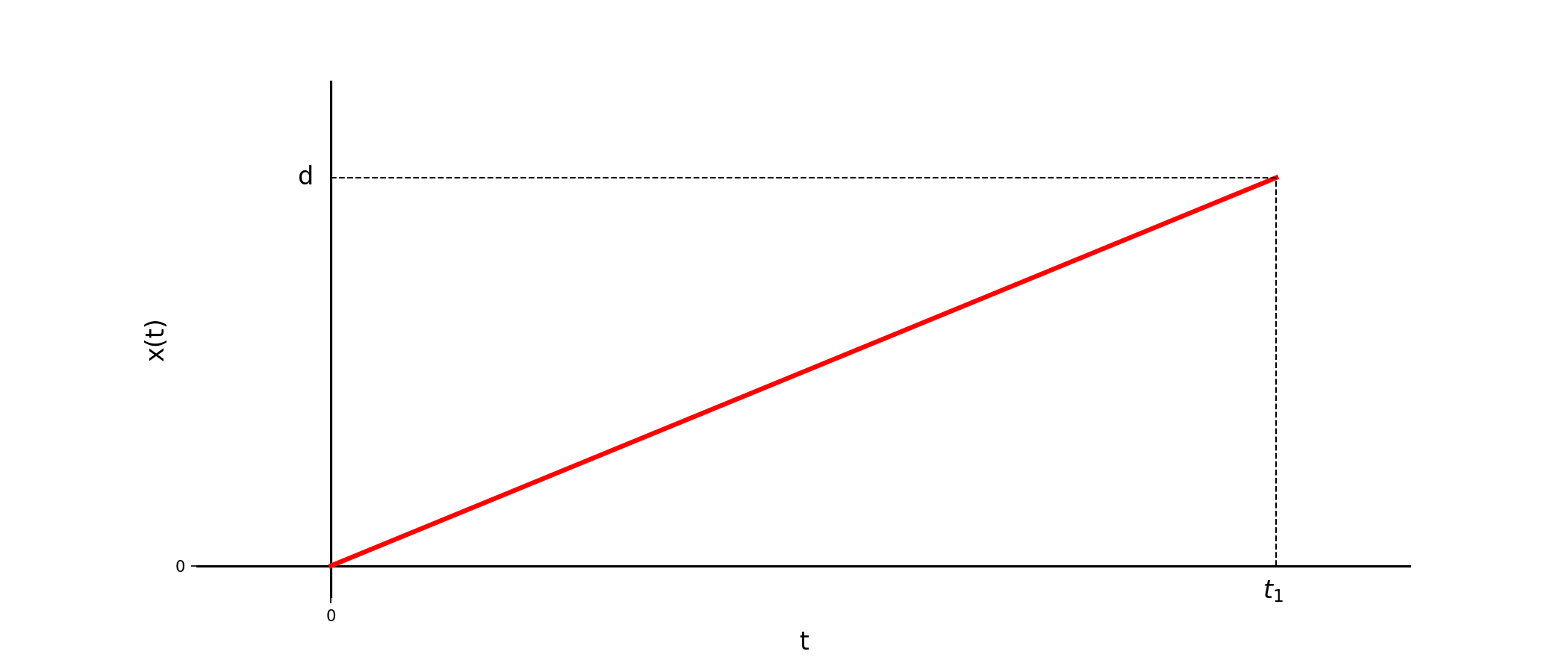
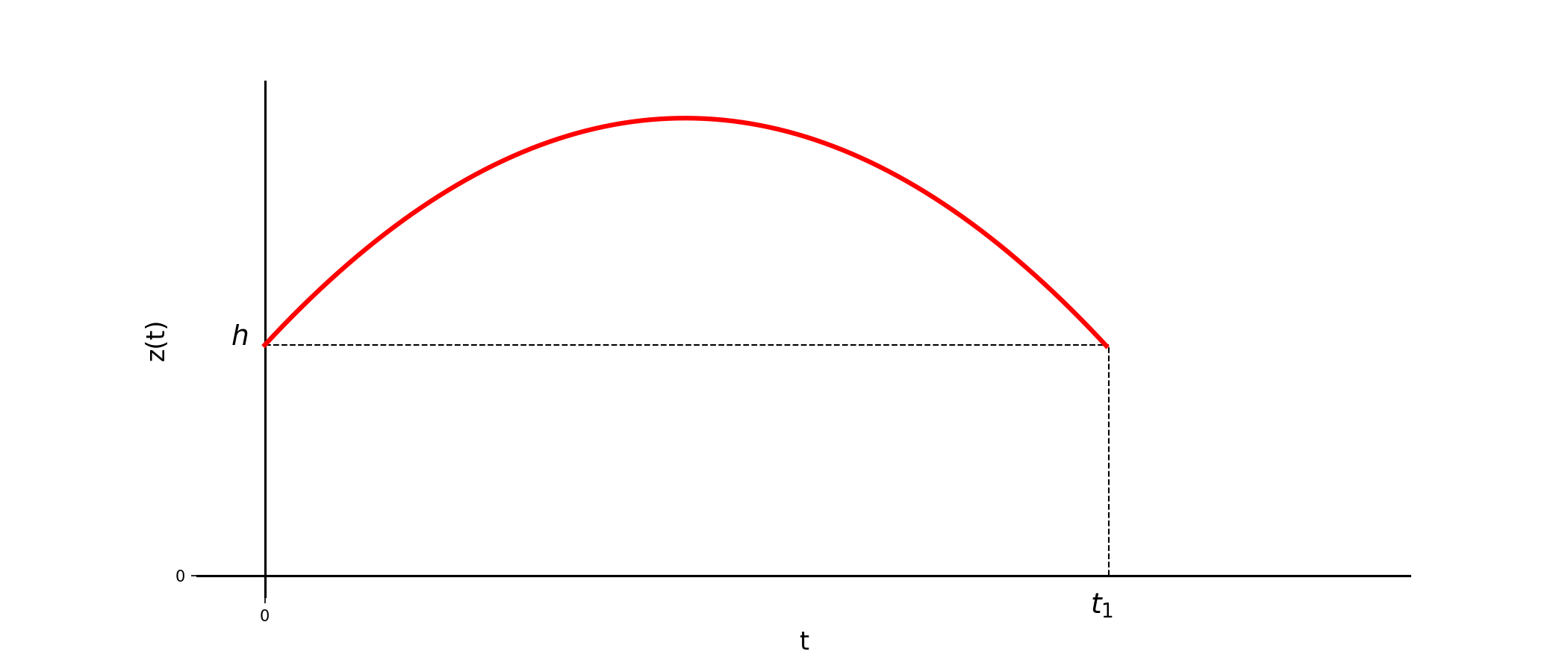
A.2.4 Vol parabolique \((\ast \ast)\)

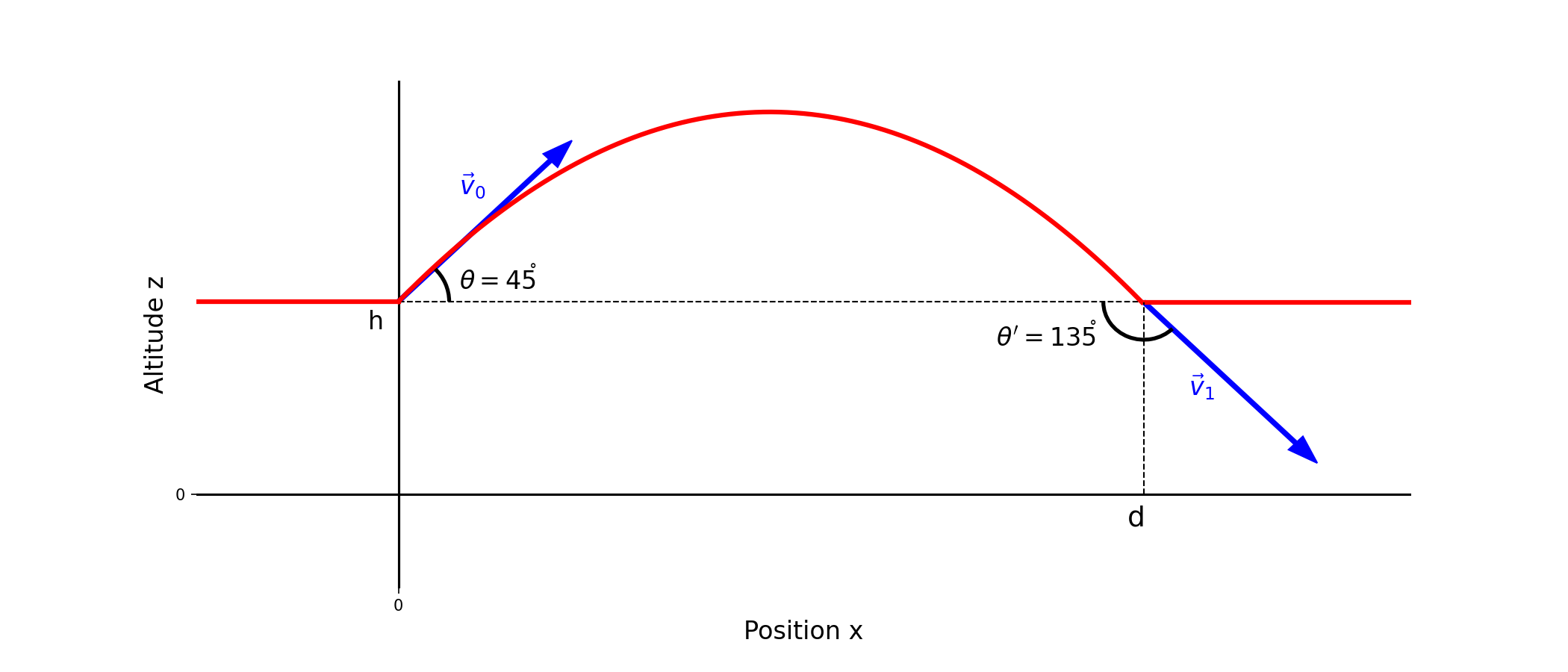
Les effets de l’apesanteur peuvent être étudiés lors de vols dits « paraboliques » — voir la figure 1.1(a). Le vol se déroule de la façon suivante : après une phase d’ascension, le pilote coupe les gaz lorsque la trajectoire de l’avion fait un angle \(\theta=\frac{\pi}{4}\) avec l’horizontale. L’avion entame alors la phase parabolique au cours de laquelle l’accélération est constante.

On suppose que l’avion évolue dans le plan \(Oxz\), l’axe vertical \((Oz)\) étant orienté vers le haut. L’origine du repère coïncide avec la position de l’avion à l’instant \(t=0\) où débute la phase d’apesanteur. On note \(v_0\) la norme de la vitesse à l’instant initial.

1. Faire un schéma représentant le repère ainsi que le vecteur vitesse \(\vec{v}_0\) à l’instant initial \(t=0\). Déterminer les composantes de \(\vec{v}_0\) en fonction de \(v_0\) et \(\theta\).

2. Au cours de la phase parabolique (\(t\geq 0\)), le vecteur accélération est donné par \(\vec{a}=-g \vec{e}_z\), où \(g\) est l’accélération de la pesanteur. Déterminer l’expression des composantes \(v_x(t)\), \(v_y(t)\) et \(v_z(t)\) de la vitesse pour \(t\geq 0\).

3. En déduire les équations horaires \(x(t)\), \(y(t)\) et \(z(t)\). On prendra soin de préciser les conditions initiales afin de fixer les constantes d’intégration.

4. Tracer les courbes représentatives des fonctions \(x(t)\), \(y(t)\) et \(z(t)\).

5. Question Bonus 1 \((\ast \ast \ast)\): Montrer que la trajectoire de l’avion est une parabole. Tracer la courbe** \(z(x)\)

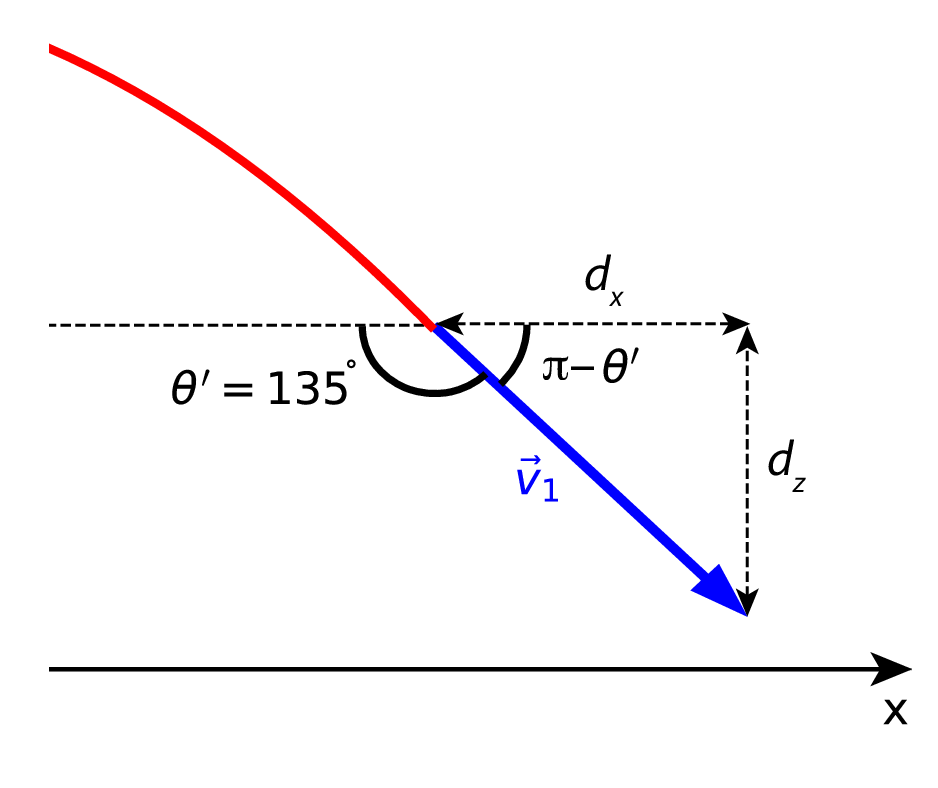
6. Question Bonus 2 \((\ast \ast \ast)\): Le pilote remet les gaz lorsque la trajectoire de l’avion fait l’angle complémentaire** \(\theta'=135^\circ\) avec l’horizontale. Calculer la distance horizontale parcourue par l’avion lors de la phase parabolique. Pour l’application numérique, on prendra : \(v_0=700\) km/h et \(g=9,81~\text{m}\cdot\text{s}^{-1}\).

Fig. 50 Gauche: (a) Airbus A310 « Zéro G » du CNES, basé à l’aéroport de Bordeaux-Mérignac (crédit photo : airzerog.com). Droite: (b) Hémisphère Nord vu depuis la verticale du pôle.

Solution

Question 1.

Fig. 51 \(z(x)\)

Vitesse initiale:

\[\begin{split}\vec{v}(0) &= v_0 \cos{\frac{\pi}{4}} \vec{e}_{x} + v_0 \sin{\frac{\pi}{4}} \vec{e}_{z} \\ &= \frac{\sqrt{2}}{2} v_0 \vec{e}_{x} + \frac{\sqrt{2}}{2} v_0 \vec{e}_{z}\end{split}\]

Question 2.

Pour \(t\geq 0\) on a: \(\vec{a}=-g \vec{e}_{z} = \frac{d\vec{v}}{dt}\)

donc:

\[\begin{split}\begin{cases} \frac{dv_{x}}{dt}=0 \Rightarrow v_{x}(t)= C_{x} \\ \frac{dv_{y}}{dt}=0 \Rightarrow v_{y}(t)= C_{y} \\ \frac{dv_{z}}{dt}=-g \Rightarrow v_{z}(t) = -g t + C_{z} \\ \end{cases}\end{split}\]

Les conditions initiales nous permettent de déduire l’expression des constantes:

\[\begin{split}\begin{cases} v_{x}(0) = \frac{\sqrt{2}}{2} v_0 = C_{x} \\ v_{y}(0) = 0 = C_{y} \\ v_{z}(0) = \frac{\sqrt{2}}{2} v_0 = C_{z} \\ \end{cases}\end{split}\]

d’où finalement:

\[\begin{split}\boxed{ \begin{cases} v_{x}(t)=\frac{\sqrt{2}}{2} v_0 \\ v_{y}(t) = 0 \\ v_{z}(t) = -g t + \frac{\sqrt{2}}{2} v_0 \\ \end{cases} }\end{split}\]

Question 3.

Pour obtenir les équations horaires, nous allons intégrer l’expression de la vitesse:

\[\begin{split}\vec{v} = \frac{d\vec{r}}{dt} = \begin{cases} \frac{dx}{dt}=\frac{\sqrt{2}}{2} v_0 \Rightarrow x(t) = \frac{\sqrt{2}}{2} v_0 t + C'_{x} \\ \frac{dy}{dt}= 0 \Rightarrow y(t) = C'_{y} \\ \frac{dz}{dt}=-g t + \frac{\sqrt{2}}{2} v_0 \Rightarrow z(t) = -\frac{1}{2} g t^2 + \frac{\sqrt{2}}{2} v_0 t + C'_{z} \end{cases}\end{split}\]

Comme toujours on utilise les conditions initiales pour exprimer les constantes: en \(t=0\) nous avons:

\[\begin{split}\begin{cases} x(0) = 0 = C'_{x} \\ y(0) = 0 = C'_{y} \\ z(0) = h = C'_{z} \end{cases}\end{split}\]

et donc finalement:

\[\begin{split}\boxed{ \begin{cases} x(t) = \frac{\sqrt{2}}{2} v_0 t \\ y(t) = 0 \\ z(t) = -\frac{1}{2} g t^2 + \frac{\sqrt{2}}{2} v_0 t + h \end{cases} }\end{split}\]

Question 4.

Fig. 52 \(x(t)\)

Fig. 53 \(y(t)\)

Fig. 54 \(z(t)\)

Question Bonus 1:

La trajectoire de l’avion est donnée par \(z(x)\). Exprimons \(t(x)\)

\(x(t)= \frac{\sqrt{2}}{2} v_0 t \Rightarrow t(x)= \frac{\sqrt{2}}{v_0} x\)

puis injectons dans l’expression de \(z(t)\):

\[\begin{split}z(x) &=-\frac{1}{2} g \Big(\frac{\sqrt{2}}{v_0} x\Big)^2 + \frac{\sqrt{2}}{2} v_0 \Big(\frac{\sqrt{2}}{v_0} x\Big) + h\\ &= -\frac{1}{2} g \frac{2}{v_0^2} x^2 + x + h\end{split}\]

soit finalement:

(58)\[\boxed{z(x)=-\frac{g}{v_0^2} x^2 + x + h}\]

Il s’agit bien de l’équation d’une parabole.

Question Bonus 2:

Fig. 55 \(\tan{\pi-\theta'}=\frac{dz}{dx}=-\tan{\theta'}\)

Par définition de la tangente, on a: \(\tan{\pi-\theta'}=\frac{dz}{dx}=-\tan{\theta'}\) (voir Fig. 55). En injectant l’expression de \(z(x)\) établie dans l’équation (58), on obtient:

\(-\tan{\theta'}=-\frac{2g}{v_0^2} x + 1\)

Lorsque \(\theta'=135^{\circ}\), alors on est à la distance \(d\) et \(tan{\theta'}= -1=-\frac{2g}{v_0^2} d + 1\), d’où finalement:

\(\boxed{d=\frac{v_0^2}{g}}\).

Application numérique: \(v_0=700 \text{km/h} = 194.4 m\cdot s^{-1} \Rightarrow \boxed{d=3854m}\)

A.2.5 Rotation de la Terre \((\ast \ast)\)

La Terre, assimilée à une sphère de rayon \(R=6400\) km, tourne sur elle-même avec la période \(T=24\) h. Vu depuis l’espace, un point à la surface de la Terre est animé d’un mouvement circulaire uniforme. On souhaite déterminer sa vitesse en fonction de la latitude \(\lambda\) [1].

1. Calculer la vitesse angulaire de rotation de la Terre.

2. Déterminer le rayon d’un parallèle terrestre en fonction de sa latitude \(\lambda\) (voir la Fig. 50 (b)).

3. En déduire la vitesse \(v\) d’un observateur selon qu’il se trouve au niveau de l’équateur (\(\lambda=0^{\circ}\)), à Bordeaux (\(\lambda = 45^{\circ}\)) ou au Pôle Nord (\(\lambda=90^{\circ}\)).

Solution

Question 1.

La Terre fait un tour (\(=2\pi\) radians) en 1 jours (\(=24h \times 3600s = 86400s\)). Donc la vitesse angulaire de la Terre est: \(\omega=\frac{2\pi}{86400} rad\cdot s^{-1}\)

Question 2.

Exprimons le rayon du cercle à la latitude \(\alpha\) du point M, comme illustré sur la Fig. 56.

Fig. 56 Rayon en fonction de la latitude \(\alpha\) et du rayon de la Terre \(R\).

Un simple calcul trigonométrique nous donne:

\(\cos{\alpha} = \frac{r}{R} \Rightarrow r=R\cos{\alpha}\)

Question 3.

La vitesse en un point quelconque M est égale à \(v=r \omega\):

\(\boxed{v= R \cos{\alpha} \omega}\)

Applications numériques:

• À l’équateur: \(\alpha=0^{\circ} \Rightarrow v=463 m\cdot s^{-1} \approx 1668 km/h\)

• À Bordeaux: \(\alpha=45^{\circ} v=329 m\cdot s^{-1} \Rightarrow v \approx 1180 km/h\)

• Au pôle nord: \(\alpha=90^{\circ} \Rightarrow v =0 m/s = 0 km/h\)

Note: en prenant les valeur précise des latitudes de Paris et Bordeaux, on obtient:

• À Bordeaux: 330 m/s

• À Paris: 306 m/s

Conclusion: Bien que les Parisiens ont la réputation d’être toujours pressés, les Bordelais vont en fait 24 m/s plus vite que les Parisiens.

[1]

La latitude est l’angle entre un point à la surface de la Terre et le plan équatorial.