1. La corde vibrante

Introduction

L’objectif de ce TP est de vérifier expérimentalement la relation obtenue dans l’équation (55) pendant le TD1 avec un instrument à corde. Vu le matériel à notre disposition, nous souhaitons vérifier en particulier:

• de manière quantitative, la dépendance entre la longueur de la corde et la fréquence, tous les autres paramètres étant constants

• de manière qualitative, la dépendance entre la masse linéïque de la corde et la fréquence, tous les autres paramètres étant constants

• de manière qualitative, la dépendance entre la tension de la corde et la fréquence, tous les autres paramètres étant constants

Pour cela, nous aurons besoin du matériel suivant:

• une guitare (ou tout autre instrument à corde).

• une règle ou un mètre

• un appareil de mesure de la fréquence des sons

• un outil pour tracer des courbes (tableur, calculatrice, Python, ou du papier millimétré)

Matériel

L’instrument

Vous avez le choix entre:

• utiliser un instrument à corde que vous possédez

• emprunter une guitare ou un ukulele à l’OpenLAB.

• fabriquer votre instrument à corde avec une boite de carton et un élastique, en suivant les instructions de la vidéo disponible sur le Moodle.

Mesure de la fréquence d’un son: utilisation de PhyPhox

La fréquence du son émis par la guitare peut être mesurée avec un smartphone et l’application PhyPhox.

Après avoir installé PhyPhox sur votre télephone, vous pourrez accéder à l’étude du spectre des sons en choisissant « Audio Spectrum » dans le menu principal (Fig. 65)

Fig. 65 Menu principal de PhyPhox.

L’outil « Audio Spectrum » permet de mesurer le spectre d’un son. Une fois dans l’outil, lancer l’acquisition en cliquant sur la flèche en haut a droite (Fig. 66). L’acquisition commence alors et mesure le spectre des bruits et sons ambiants autour de vous.

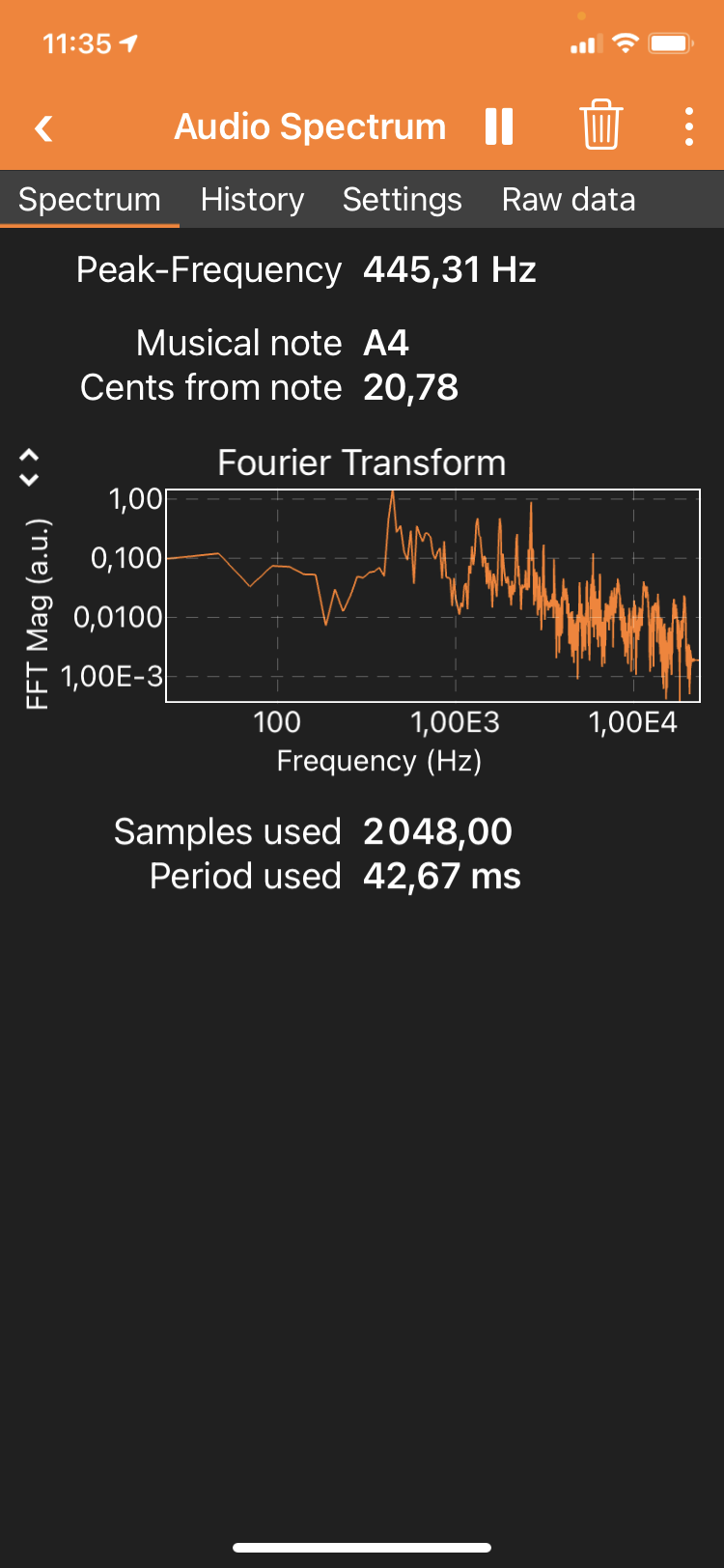
Fig. 66 Application « Audio Spectrum »de PhyPhox

Rappels

Les sons usuels sont composés de nombreuses fréquences. Le spectre du son nous donne l’intensité respective de chaque fréquence présente dans le son. Dans le cas d’un instrument de musique, le son correspondant à note est relativement « pur », au sens ou il ne contient (quasiment) qu’une seule fréquence.

Acquisition des mesures

Pour continuer notre expérience, prenez soin de faire le silence autour de vous. Pincez une des cordes de la guitare. Vous verrez alors un spectre très « piqué », tel que celui présenté dans la Fig. 66. Le pic principal correspond à la fréquence principal de la note jouée, et sa valeur est indiquée « Peak Frequency », ici 445.31 Hz, ce qui correspond (à peu prêt) à la note la (dont la fréquence exacte est 440 Hz).

Les fréquences ont comme dimension l’inverse d’un temps \([T^{-1}]\). Leur dimension en unité S.I. est donc la \(s^{-1}\), mais pour des raisons historiques cette unité S.I. a été appelée le Hertz, en l’honneur du physicien allemand Heinrich Hertz qui découvrit et étudia les ondes radioélectriques. On a donc tout simplement 1Hz=1\(s^{-1}\).

PhyPhox donne également la valeur de la note la plus proche de la fréquence principale, dans le système de notation anglo-saxon basé sur les lettres de l’alphabet. Ainsi dans la Fig. 66 la note la plus proche est A4, qui correspond à un la de quatrième octave dans le système français.

Expérience 1: étude de la dépendance de la fréquence en fonction de \(l\):

Le seul paramètre qui doit varier est la longueur de la corde \(l\). Nous allons donc choisir une corde de la guitare, régler sa tension une fois pour toute, puis mesurer la fréquence de la note obtenue en pinçant cette corde pour différentes valeurs de sa longueur.

Pour faire varier la longueur effective de la corde, le musicien peut simplement presser la corde contre les frettes, comme illustré dans la Fig. 67 . La longueur effective de la corde (c’est à dire la longueur de la corde qui va vibrer et produire la note) sera égale à la distance entre le sillet du chevalet et le frette (voir Fig. 67)

Fig. 67 Le musicien change la longueur de la corde en pinçant la corde sur les frettes.

Protocole

Le protocole expérimental sera donc le suivant:

1. choisir un frette

2. mesurer la distance entre ce frette et le sillon de chevalet. Cela nous donne la longueur de la corde \(l\)

3. pincer a corde et mesurer la fréquence de la note avec PhyPhox

4. choisir le frette suivant, et recommencer

On pourra alors remplir le tableau ci-dessous:

Tableau 7 Mesures: fréquence et fonction de la longueur de la corde

Longueur de la corde	Fréquence
…	…
…	…
…	…

En utilisant un tableur , ou Python (voir ci-dessous), ou du papier millimétré, tracer la courbe de la fréquence en fonction de \(\frac{1}{l}\). D’après le résultat obtenu dans l’équation (55), lorsque tous les autres paramètres sont constants la fréquence doit être proportionnelle à l’inverse de la longueur. On devrait donc avoir une droite, comme dans l’exemple de la Fig. 68. On peut aussi vérifier que lorsque la longueur double, la fréquence diminue d’un facteur 2.

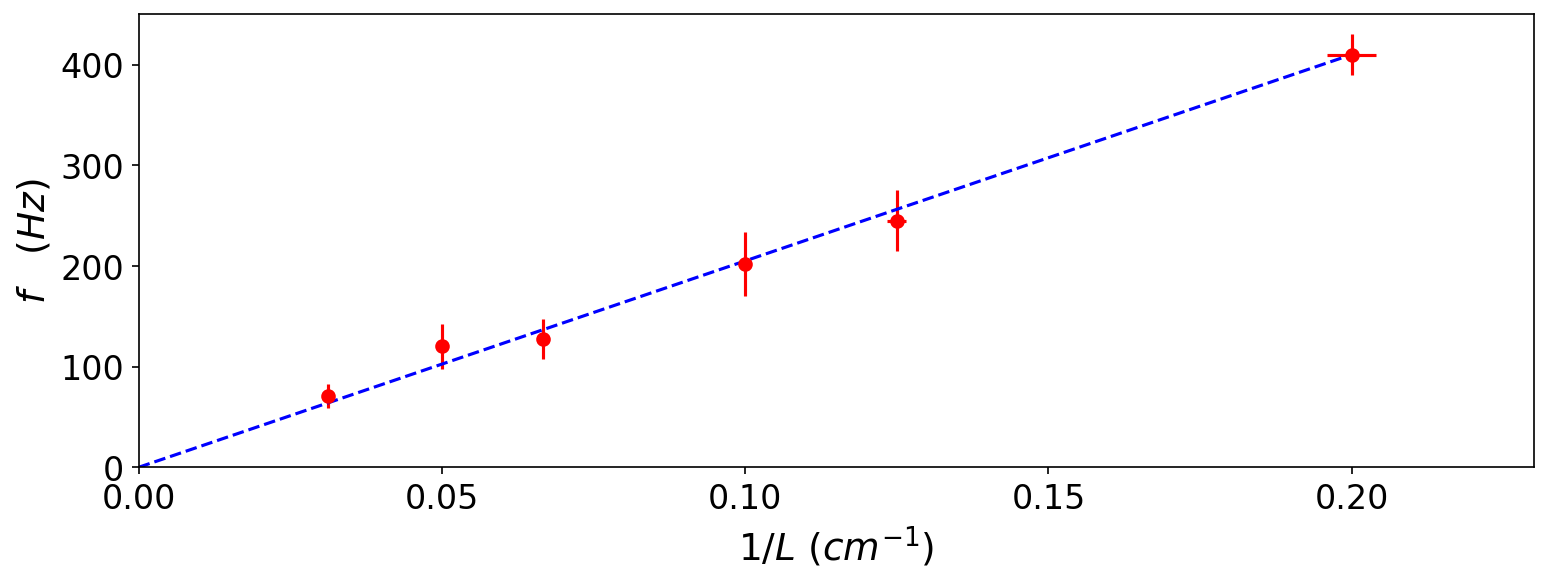
Fig. 68 Exemples de mesures de fréquences en fonction de l’inverse de la longueur de la corde.

Code Python

# Importer les libraries nécessaires
import matplotlib.pyplot as plt
import numpy as np

# Les mesures (inventées)
L=[5,8,10,15,20,32]  # longueur en cm
err_L=[0.1,0.1,0.1,0.1,0.1,0.1] # incertitude sur L, 1mm pour toutes les mesures
f=[410., 245. , 202. , 127., 120. ,70.5] # fréquence en Hz
err_f=[20,30,32,20,22,12] # incertitudes sur f

# Initialiser une figure, de taille 12x4
fig, ax = plt.subplots(figsize=(12,4))

# Tracer les points, avec leurs barres d'erreur
plt.errorbar(1/L, f, yerr=err_f, xerr=err_L/L * 1/L ,fmt='or')
# Relation théorique (inventée aussi)
plt.plot([0,0.2],[0,400],'--',color='b')

# Titres sur les axes
plt.xlabel(r'$1/L\ (cm^{-1})$',fontsize=18)
plt.ylabel(r'$f\ \ \ (Hz)$',fontsize=18)
# Taille des chiffres sur les axes
ax.tick_params(axis='both', which='major', labelsize=16)
# Limite des axes
plt.xlim(0,0.23)
plt.ylim(0,450)

# Sauver la figure
plt.savefig('ma_figure.png',bbox_inches='tight',dpi=150)

Expérience 2: étude de la dépendance de la fréquence en fonction de \(\mu\):

Le seul paramètre qui doit varier est la masse linéïque de la corde \(l\). Nous n’avons pas la possibilité de mesurer la masse linéïque des cordes de notre guitare et faire une étude quantitative, mais nous savons que les cordes les plus grosses doivent avoir une masse linéïque plus grande. Nous pouvons donc comparer qualitativement la fréquence des notes produites par deux cordes.

En toute rigueur pour faire cette étude nous devrions nous assurer que la tension des différentes cordes de la guitare est la même. Malheureusement nous n’avons pas les outils pour mesurer la tension des cordes, et devrons faire l’hypothèse (plus ou moins vraie) que la tension des cordes est la même. En comparant la corde la plus fine avec la corde plus grosse, nous allons maximiser l’écart de masse linéïque, et ainsi réduire l’influence relative des éventuelles différences de tension.

Le protocole expérimental sera donc le suivant:

1. Pincer la corde la plus fine. On notera \(\mu_{0}\) sa masse linéïque.

2. Mesurer la fréquence de la note avec PhyPhox

3. Pincer la corde la plus grosse. On notera \(\mu_{1}\) sa masse linéïque.

4. Mesurer la fréquence de la note avec PhyPhox

On pourra alors remplir le tableau ci-dessous:

Tableau 8 Mesures: fréquence et masse lineïque

Corde	Fréquence
fine (\(\mu_0\))	…
grosse (\(\mu_1>\mu_0\))	…

La grosse la plus grosse (\(\mu_{1}\)) émet un son plus grave, c’est à dire une fréquence plus basse, que la corde fine (\(\mu_{0}\)). On trouve donc bien, de manière qualitative, que la fréquence varie diminue quand la masse linéïque augmente.

Notre expérience ne nous permet pas de conclure plus en détail et de démontrer que cette dépendance varie comme l’inverse de la racine carrée de la masse linéïque, puisqu’on ne connait pas les valeurs exactes de \(\mu_{0}\) et \(\mu_{1}\).

Expérience 13: étude de la dépendance de la fréquence en fonction de \(T_{en}\):

Le seul paramètre qui doit varier est la tension \(T_{en}\) de la corde. Nous N’avons pas la possibilité de mesurer cette force, mais nous savons qu’en tournant le chevalet dans un sens ou dans l’autre nous pouvons l’augmenter ou la diminuer. Nous pourrons donc vérifier qualitativement si la fréquence augmente avec la tension, comme prévue par l’équation (55).

Le protocole expérimental sera donc le suivant:

1. Choisir une corde

2. Pincer la corde et mesurer la fréquence de la note avec PhyPhox. On notera \(T_{en}^{0}\) la tension pour cette mesure.

3. Tendre la corde avec le chevalet (par exemple faire 1 tour de chevalet), pincer la corde et mesurer la fréquence de la note avec PhyPhox. On notera \(T_{en}^{+1}\) la tension pour cette mesure.

4. Détendre la corde avec le chevalet (par exemple faire 2 tour de chevalet dans l’autre sens!), pincer la corde et mesurer la fréquence de la note avec PhyPhox. On notera \(T_{en}^{-1}\) la tension pour cette mesure.

On pourra alors remplir le tableau ci-dessous:

Tableau 9 Mesures: fréquence et tension, avec \(T_{en}^{-1}<T_{en}^{0}<T_{en}^{+1}\)

Corde	Fréquence
\(T_{en}^{0}\)	…
\(T_{en}^{+1}\)	…
\(T_{en}^{-1}\)	…

Cette expérience ne nous permet pas non plus de démontrer que la fréquence varie comme la racine carrée de la tension, puisqu’on ne connaît pas les valeurs exactes de \(T_{en}^{-1}\), \(T_{en}^{0}\) et \(T_{en}^{+1}\). Mais comme nous savons que \(T_{en}^{-1}<T_{en}^{0}<T_{en}^{+1}\), on peut tout de même vérifier que la fréquence diminue quand la tension diminue (et vice versa).