A. 5. La gravitation
A.5.1) Force gravitationnelle (\(\ast\) - 5min)
Calculer l’intensité de la force d’attraction gravitationnelle entre :
deux atomes de masse \(m=10^{-26}\) kg, séparés de la distance \(d=1~\)Å.
deux bactéries (\(m=10^{-15}\) kg) séparées de la distance \(d=1~\mu\text{m}\).
deux grains de sable (\(m=10^{-9}\) kg) séparés de la distance \(d=1~\text{mm}\).
deux avions Airbus A380 (\(m=560\) tonnes) séparés de la distance \(d=10~\text{m}\).
les deux étoiles principales du système Alpha du Centaure, de masse \(m_A\simeq 2.2\times 10^{30}\) kg et \(m_B\simeq 1.8\times 10^{30}\) kg, séparées de la distance \(d\simeq5,4\times 10^9\) km.
A.5.2) Atome d’hydrogène (\(\ast \ast \ast\) - 30∼45min)
L’atome d’hydrogène est constitué d’un électron, de masse \(m_e \approx 9.1\times 10^{-31}\) kg et de charge \(q_e=-e\), en interaction avec un proton, de masse \(m_p\approx 1.67\times 10^{-27}\) kg et de charge \(q_p=+e\) (\(e\approx 1,6 \times 10^{-19}~\text{C}\)). Le proton et l’électron sont séparés de la distance \(r\). On note \(\vec{u}\) le vecteur unitaire orienté du proton vers l’électron. Outre l’attraction gravitationnelle, le proton exerce sur l’électron la force de Coulomb :
où \(\varepsilon_0 \approx 8,85 \times 10^{-12}\) SI est la permittivité du vide.
A.5.2.1) Modèle classique
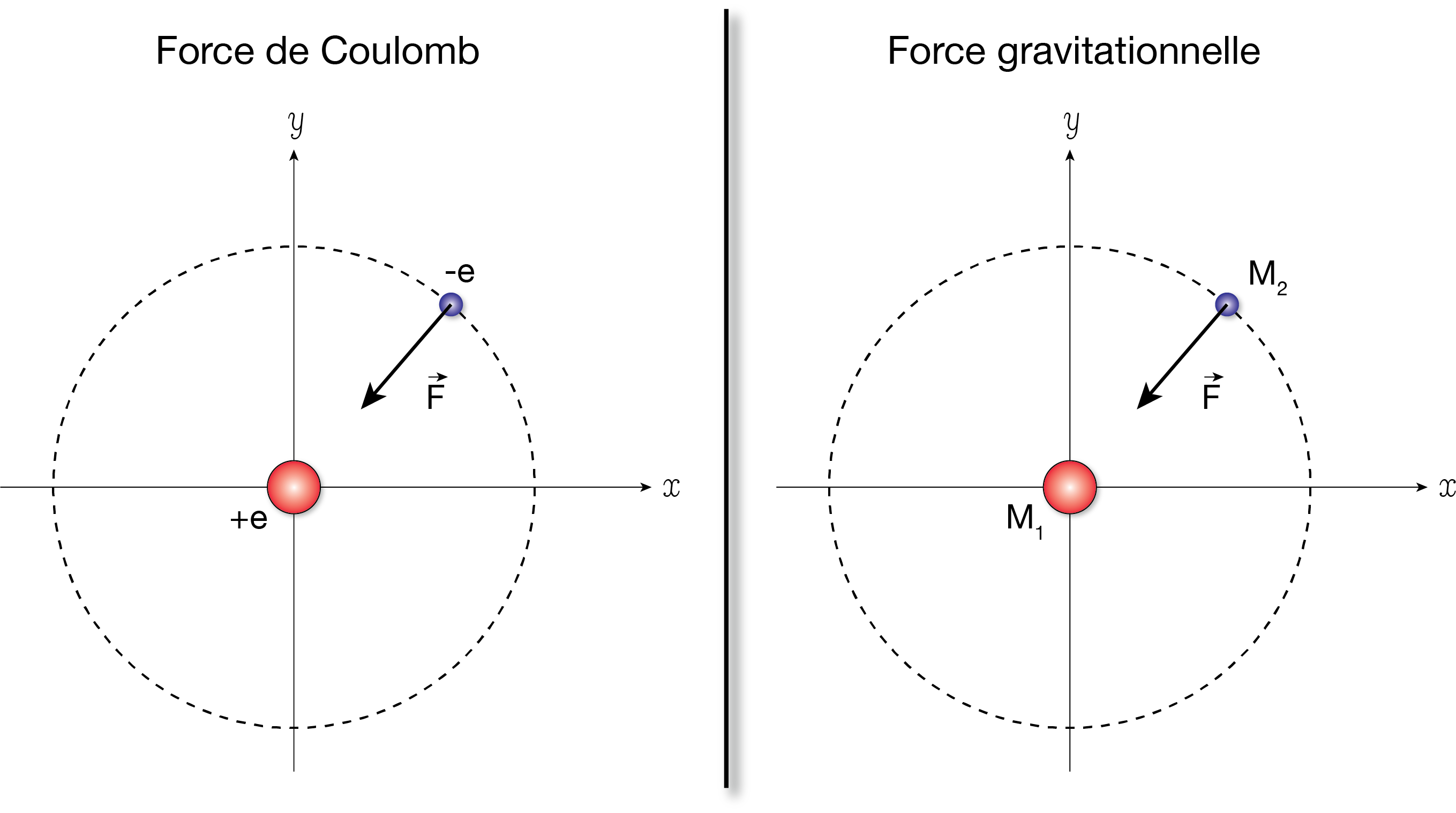
Faire un schéma du problème. Discuter les similitudes et les différences entre la force coulombienne et la force gravitationnelle.
Comparer l’intensité des deux forces pour \(r=1\) Å. Quelle force peut-on négliger ?
La masse du proton étant grande devant celle de l’électron, on suppose que l’électron a un mouvement circulaire uniforme autour du proton que l’on choisit comme origine du repère. En appliquant le principe fondamental de la dynamique, déterminer la vitesse de l’électron.
En déduire la relation entre la période du mouvement et le rayon \(R\) de la trajectoire.
A.5.2.2) Modèle quantique
Au niveau microscopique, les propriétés des particles élémentaires sont décrites par la physique quantique qui fait intervenir la constante de Planck \(h\approx 6.62\times 10^{-34}~\text{J}\cdot \text{s}\). Sans entrer dans le formalisme de cette théorie, nous allons estimer la taille de l’atome d’hydrogène en utilisant l’analyse dimensionnelle.
À partir de l’expression de la force \(\vec{F}_c\), déterminer la dimension de \(\varepsilon_0\).
On suppose une relation de la forme : \(R = f(e,m_e,h,\varepsilon_0)\). En déduire que le rayon de l’atome d’hydrogène est proportionnel au rayon de Bohr \(a_0\) :
\[a_0 = \frac{\varepsilon_0 h^2}{\pi m_e e^2} \ .\]Calculer la valeur numérique du rayon de Bohr.