A.4. Dynamique du point

A.4.1) Mouvement sur un plan incliné (\(\ast \ast\) - 20∼30min)

On considère un mobile de masse \(m\), assimilé à un point matériel \(M\), qui se déplace sur un plan incliné faisant un angle \(\beta\) avec l’horizontale. On suppose que les forces de frottement sont négligeables. On se place dans le repère cartésien \(Oxyz\) représenté sur la Fig. 61.

1. Définir le système étudié et faire le bilan des forces.

2. En projetant le principe fondamental de la dynamique sur les axes du repère, montrer que l’on obtient le système d’équations :

   \[\frac{ d v_x}{d t} =0 \ , \quad \frac{ d v_y}{d t} = -g \sin \beta \ , \quad \text{et} \quad \frac{ d v_z}{d t} = -g \cos \beta + \frac{1}{m} R_n \ .\]

3. Que peut-on dire du mouvement suivant \((Oz)\) ? Quelle est la nature du mouvement selon les directions \((Ox)\) et \((Oy)\) ?

Le mobile est lancé à l’instant \(t=0\) depuis l’origine \(O\) des coordonnées, avec une vitesse initiale \(\vec{v}_0\) faisant un angle \(\alpha\) avec l’axe \(\vec{e}_x\).

4. Déterminer les expressions des composantes \(v_x(t)\) et \(v_y(t)\) de la vitesse. On tiendra compte des conditions initiales.

5. En déduire les équations horaires \(x(t)\) et \(y(t)\) du mouvement.

6. Déterminer finalement l’équation de la trajectoire \(y(x)\). Comparer avec le mouvement de chute libre discuté dans le cours.

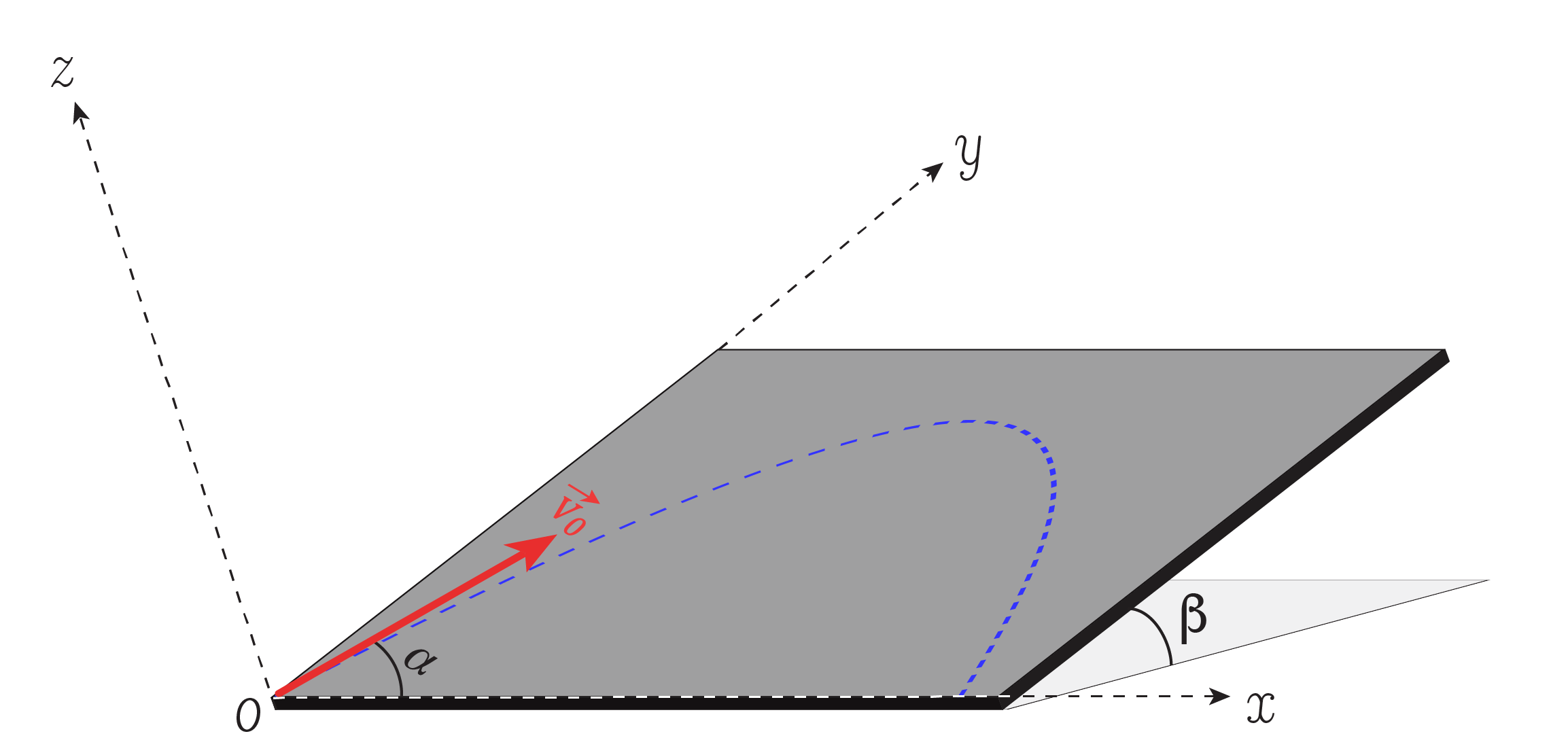
Fig. 61 Mouvement sur un plan inclinée

Solution

Question 1.

Le système est composé du point matériel.

Le bilan des forces s’écrit:

\[\begin{split}\vec{P} &= m \vec{g} = \begin{pmatrix}0 \\ -m g \sin{\beta} \\ -m g \cos{\beta}\end{pmatrix} \\ \vec{R}_{n} &= \begin{pmatrix}0 \\0 \\ R_{n}\end{pmatrix} \\\end{split}\]

Question 2.

Le principe fondamental de la dynamique s’écrit: \(\vec{P}+\vec{R}_n=m \vec{a}\). En projetant sur les axes de notre referentiel:

\[\begin{split}\begin{cases} \parder{v_{x}}{t}=0 \\ \parder{dv_{y}}{t}=-g \sin{\beta} \\ \parder{v_{z}}{t}=-g \cos{\beta} + \frac{1}{m} R_{n} \end{cases}\end{split}\]

Question 3.

Le mouvement se déroulant dans le plan \(Oxy\), la trajectoire suivant \((Oz)\) est constante et on a nécéssairement: \(z=0 \Rightarrow v_{z}=0 \Rightarrow a_{z}=0\).

Selon \((Ox)\), on a \(\parder{v_{x}}{t}=0\). Le mouvement est donc uniforme.

Selong \((Oy)\), on a \(\parder{v_{y}}{t}=cte\) et donc on aura un mouvement uniformément accéléré.

Question 4.

On intègre les équations du mouvement:

Suivant \(x\):

\(\parder{v_{x}}{t}=0 \Rightarrow v_{x}(t)= C\)

or \(v_{x}(0)=v_{0} \cos{\alpha}=C\) et donc \(\boxed{v_{x}(t)=v_{0} \cos{\alpha}}\)

Suivant \(y\):

\(\parder{v_{y}}{t}=-g \sin{\beta} \Rightarrow v_{x}(t)= -g t \sin{\beta} + C'\)

or \(v_{y}(0)=v_{0} \sin{\alpha} = C'\) et donc \(\boxed{v_{y}(t)=-g t \sin{\beta} + v_{0} \sin{\alpha}}\)

Question 5.

On intègre les composantes de la vitesse déterminer précédemment:

\(v_{x}(t)=\parder{x}{t}=v_{0} \cos{\alpha} \Rightarrow x(t) = v_{0} t \cos{\alpha} + C_1\)

Comme on a \(x(0)=0=C_1\) on obtient \(\boxed{x(t)=v_{0} t \cos{\alpha}}\)

\(v_{y}(t)=\parder{y}{t}=-g t \sin{\beta} + v_{0} \sin{\alpha} \Rightarrow y(t) = -\frac{1}{2} g t^2 \sin{\beta} + v_{0} t \sin{\alpha} + C_2\)

Comme on a \(y(0)=0=C_2\) on obtient \(\boxed{y(t)=-\frac{1}{2} g t^2 \sin{\beta} + v_{0} t \sin{\alpha}}\)

Question 6.

Exprimons \(t\) en fonction de \(x\)

\(x(t)=v_{0} t \cos{\alpha} \Rightarrow t=\frac{x}{v_{0} \cos{\alpha}}\)

puis injectons dans l’équation de \(y\):

\(y(x)=-\frac{1}{2} g \Big(\frac{x}{v_{0} \cos{\alpha}}\Big)^2 \sin{\beta} + v_{0} \Big(\frac{x}{v_{0} \cos{\alpha}}\Big) \sin{\alpha}\)

et donc finalement après simplification:

\(\boxed{y(x)=-\frac{g \sin{\beta}}{2v_{0}^2 \cos^2{\alpha}}x^2 + x \tan{\alpha}}\)

A.4.2) Chute libre avec frottement fluide (\(\ast \ast\) - 35∼45min)

On étudie la chute d’une microbille de verre (rayon \(a=1\) \(\mu\)m, masse \(m=10^{-14}\) kg) dans l’eau (\(\eta=10^{-3}~\text{Pa}\cdot\text{s}\), \(\rho=1000~\text{kg}\cdot\text{m}^{-3}\)). La poussée d’Archimède est omise dans cet exercice.

1. Faire un schéma du problème. On orientera l’axe \((Oz)\) vers le bas.

2. On suppose que la force de frottement est donnée par : \(\vec{f}=-k\vec{v}\), avec \(k=6\pi \eta a\) (régime de Stokes). Montrer que la vitesse limite \(v_{\infty}\) atteinte par la bille en régime stationnaire est :

   \[v_{\infty} = \frac{mg}{6\pi \eta a} \ .\]

3. Évaluer le nombre de Reynolds correspondant : \(\text{Re} = \rho a v_{\infty}/\eta\). L’hypothèse du régime de Stokes est-elle justifiée ?

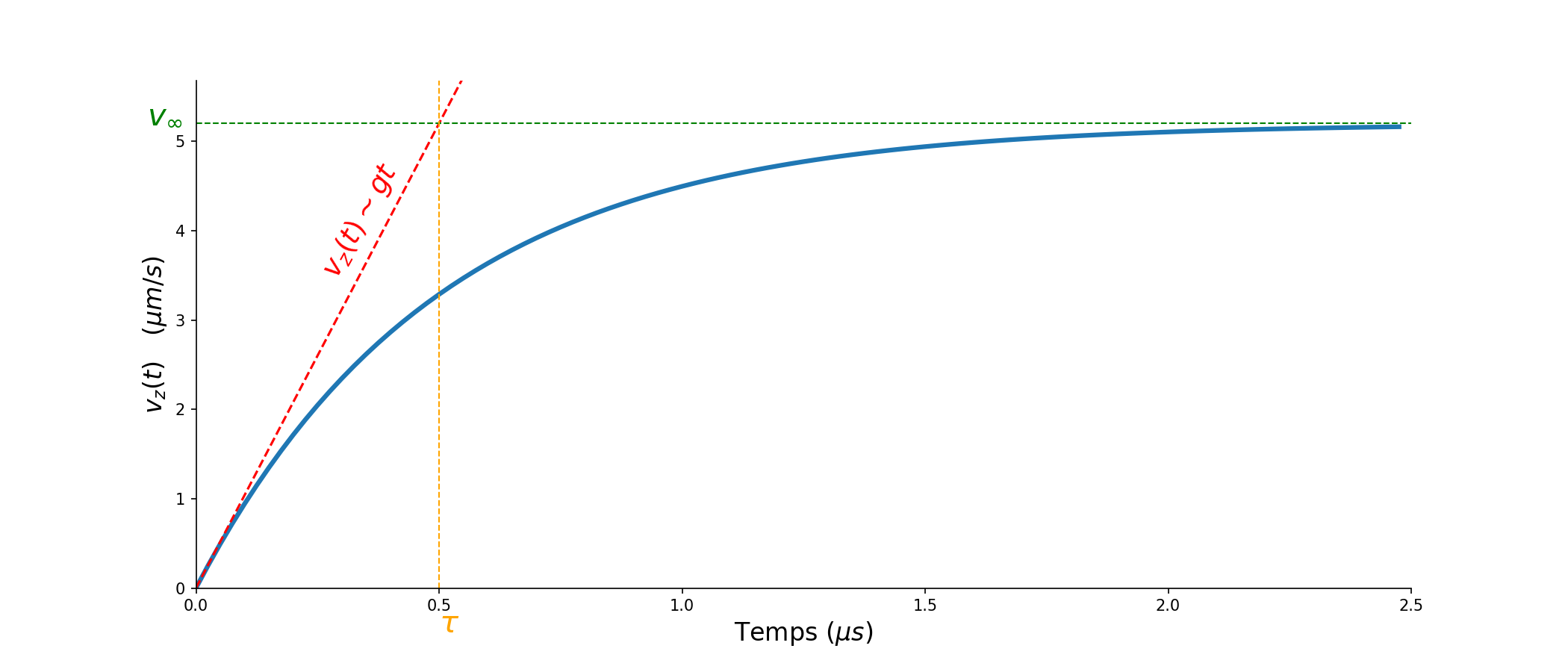
On souhaite maintenant étudier le régime transitoire. La bille est lâché de l’altitude \(z(t=0)=0\) sans vitesse initiale.

4. Établir l’équation différentielle vérifiée par la composante verticale \(v_z\) de la vitesse :

   \[\frac{d v_z}{d t} + \frac{1}{\tau} v_z = g \ ,\]

   où \(\tau\) est une constante que l’on exprimera en fonction de \(k\) et \(m\). Quelle est sa dimension ?

5. Montrer que l’équation admet une solution particulière constante, que l’on notera \(v_p\).

6. Montrer que la fonction \(v_h(t)=C e^{-t/\tau}\) est une solution de l’équation homogène (sans second membre) :

   \[\frac{d v_h}{d t} + \frac{1}{\tau} v_h =0 \ .\]

7. Montrer que la fonction : \(v_z(t) = v_h(t) + v_p\) est solution de l’équation différentielle avec second membre. En imposant les conditions initiales à cette fonction \(v_z(t)\), établir l’expression de la solution du problème.

8. Tracer la solution \(v_z(t)\). Discuter les comportement asymptotiques \(t\ll \tau\) et \(t \gg \tau\). Donner une interprétation physique à \(\tau\).

Solution

Question 1.

Fig. 62 Schéma du problème.

Le système consiste en la bille de verre que l’on assimile à un point matériel.

Question 2.

Faisons le bilan des forces: nous avons 2 forces extérieures:

\[\begin{split}\begin{cases} \vec{P}=m\vec{g}=\begin{pmatrix}0\\0\\mg\end{pmatrix} \\ \vec{f}=-k \vec{v} \\ \end{cases}\end{split}\]

On peut alors écrire le principe fondamental de la dynamique:

\[\vec{P} + \vec{f} = m \vec{a}\]

soit en projetant sur l’axe \((Oz)\):

(60)\[m \parder{v_{z}}{t} = mg - k v_z\]

Le régime stationnaire est par définition atteint lorsque la vitesse est constante, et donc: \(\parder{v_z}{t}=0\).

On en déduit:

\[\boxed{v_{\infty}=\frac{mg}{k}=\frac{mg}{6\pi\eta a}}\]

L’application numérique donne:

\[v_{\infty}=\frac{10^{-14}\times 9.81}{6\pi\times10^{-3} \times 10^{-6}}=5.2\times10^{-6} m\cdot s^{-1} = 5.2\mu m \cdot s^{-1}\]

Question 3.

D’après l’équation (60) vu en cours, le nombre de Reynolds est défini comme: \(\text{Re} = \frac{\rho V L}{\eta}\).

L’application numérique pour \(V=v_{\infty}\) et \(L=a=10^{-6}m\) s’écrit donc ici:

\[\text{Re}=\frac{1000\times 5.2\cdot 10^{-6} \times 10^{-6}}{10^{-3}}=5.2\cdot 10^{-6}\]

On voit que \(\text{Re}<<1\) et donc l’hypothèse du régime de Stokes est bien vérifiée.

Question 4

Reprenons l’équation (60):

\[\begin{split}m \parder{v_z}{t} &= mg - k v_z \\ \Leftrightarrow \parder{v_z}{t} + \frac{k}{m} v_z &= g\\\end{split}\]

soit, en posant \(\tau=\frac{m}{k}\):

(61)\[\parder{v_z}{t} + \frac{1}{\tau} v_z = g\]

La dimension de \(\tau\) est: \([\tau]=\frac{[m]}{[k]}\)

Or \([k]=\frac{[\text{Force}]}{[\text{vitesse}]}=\frac{M\cdot L \cdot T^{-2}}{L \cdot T^{-1}}=M\cdot T^{-1}\)

Donc finalement:

\[[\tau]=\frac{M}{M \cdot T^{-1}}= T\]

L’application numérique donne:

\(\tau=\frac{10^{-14}}{6\pi\cdot 10^{-3}\cdot 10^{-6}}=0.5\times10^{-6} s = 0.5\mu s\)

Question 5.

Lorsque \(v_z=v_p=\text{constante}\) , alors \(\parder{v_z}{t}=\parder{v_p}{t}=0\) et l’équation (61) s’écrit:

\[\frac{1}{\tau} v_p = g \Leftrightarrow \boxed{v_p=g \tau = \frac{g}{k} m = v_{\infty}}\]

Question 6.

En replaçant dans l’équation différentielle on trouve bien que la fonction proposée vérifie l’équation différentielle.

Question 7.

Vérifions que la fonction proposée est solution:

\[\begin{split}\parder{v_z}{t} + \frac{1}{\tau} v_z &= \overbrace{\parder{v_h}{t} +\underbrace{\parder{v_p}{t}}_{=0\\ \text{car }\\ v_p=cte}}^{= \parder{v_z}{t}} + \overbrace{\frac{1}{\tau} \Big( v_h + v_p \Big)}^{=v_z(t)} \\ &= \underbrace{\parder{v_h}{t}+\frac{1}{\tau} v_h}_{=0 \text{ (voir question 6)}} + \underbrace{\frac{1}{\tau} v_p}_{=g \text{ (voir question 5)}} &= g\end{split}\]

On vérifie donc bien que la fonction : \(v_z(t) = v_h(t) + v_p\) est solution de l’équation différentielle avec second membre.

Les conditions initiales permettent d’écrire:

\[v_z(0)=0 = v_h(0)+v_p = C + v_{\infty}\]

d’où: \(C=-v_{\infty}\) et finalement:

\[\boxed{v_z(t)=v_{\infty} (1- e^{-t/\tau})}\]

Question 8.

Fig. 63 Courbe de la vitesse \(v_z(t)\)

• Pour \(t<<\tau\): alors \(e^{-t/\tau}\approx 0\) et on est dans un régime où les frottements sont négligeables et le mouvement est quasiment un mouvement de chute libre \(v_z(t)\approx gt\). Ceci est une conséquence directe de la dépendence des frottements avec la vitesse. Au départ la vitesse est très faible et donc la force de frottement est également très faible.

• Pour \(t>>\tau\) on atteind le régime stationnaire, c’est à dire qu’il y a équilibre entre le poids et les frottements, et alors \(v_z(t)\approx v_{\infty}\).

\(\tau\) est une mesure la durée caractéristique du régime transitoire entre ces deux régimes.