4. Dynamique du point
4.1 Où est Alpha ? (\(\ast\) - 5min)
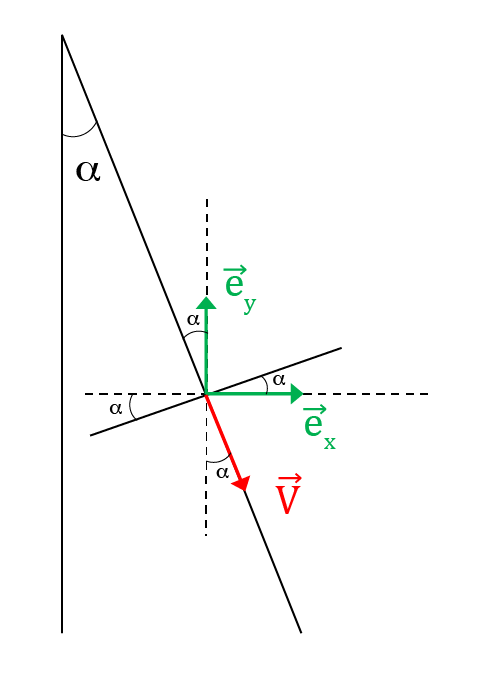
Retrouver toutes les occurrences de l’angle \(\alpha\) sur la Fig. 40 (a).
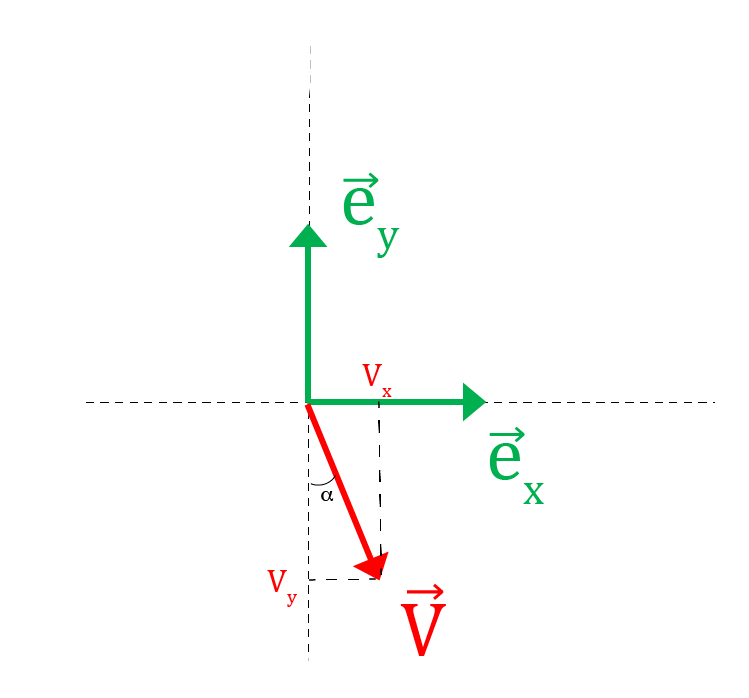
Déterminer les composantes du vecteur \(\vec{V}\) dans la base \((\vec{e}_x, \vec{e}_y)\) en fonction de \(V=\Vert \vec{V} \Vert\) et \(\alpha\).
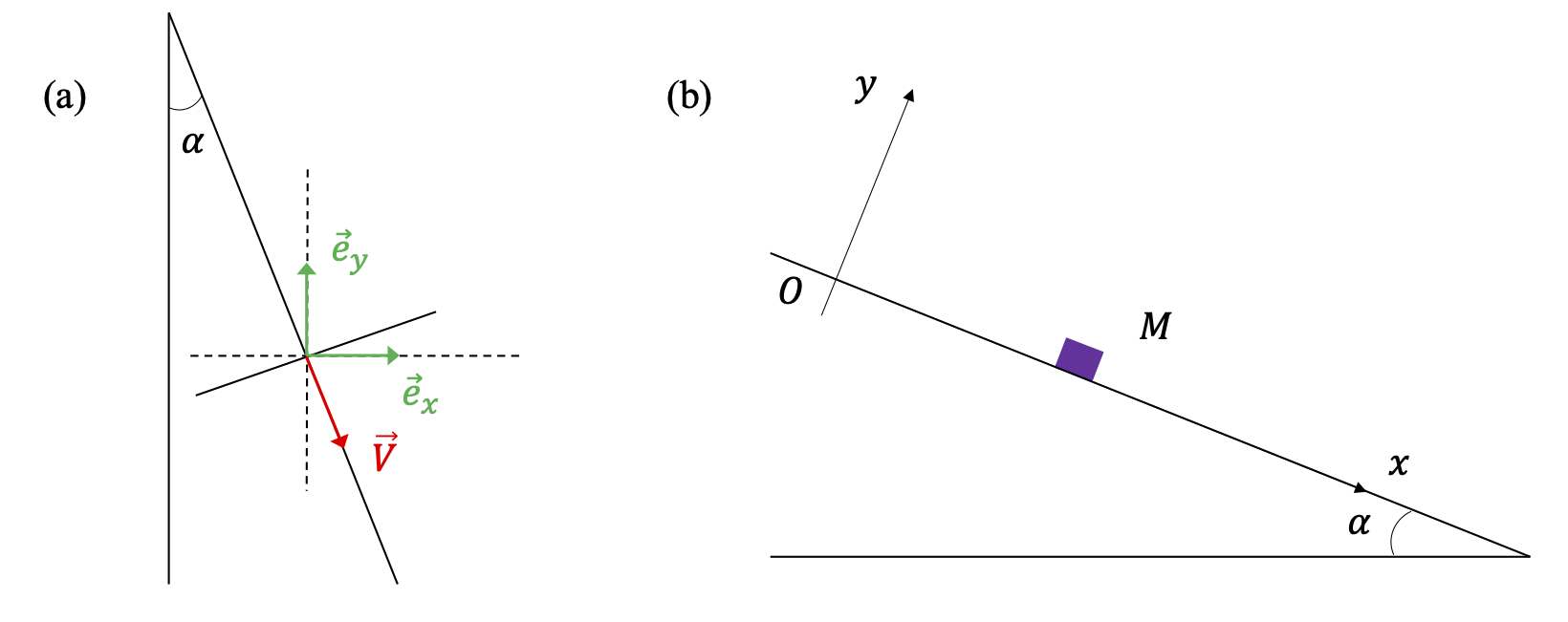
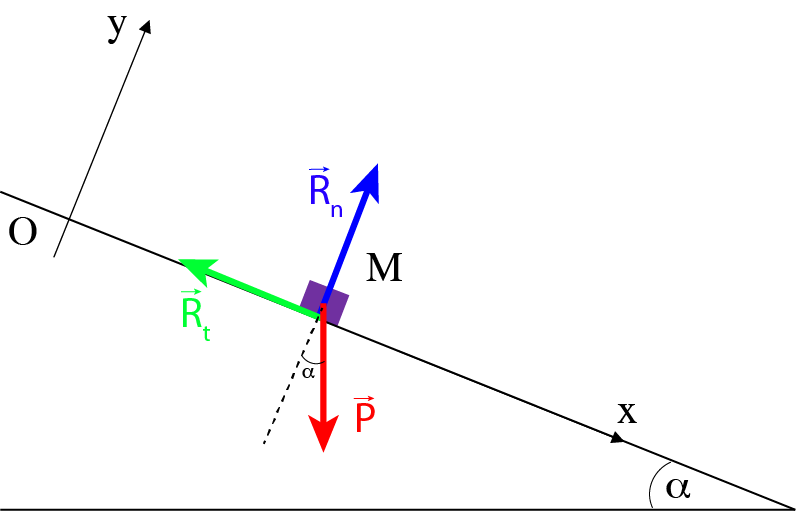
Fig. 40 Gauche: (a) Projection d’un vecteur. Droite: (b) Mouvement en présence de frottement solide.
4.2 Mouvement d’un skieur (\(\ast\ast\) - 20~30 min)
On étudie l’effet du frottement solide sur le mouvement d’un skieur, que l’on modélise par un point matériel \(M\) qui se déplace le long d’un plan incliné. On se place dans le repère cartésien \(Oxy\) représenté sur la Fig. 40 (b). On note \(m\) la masse du point matériel, \(\mu\) le coefficient de frottement solide, et \(\alpha\) l’angle du support avec l’horizontale. On néglige les forces de frottement fluide.
Faire le bilan des forces et les représenter sur le schéma.
Déterminer les composantes des forces dans le repère \(Oxy\).
Rappeler la loi de Coulomb.
En appliquant le principe fondamental de la dynamique, montrer que l’on obtient l’équation suivante selon la direction \((Ox)\) :
\[\frac{ d^2 x}{d t^2} =g \cos \alpha \left( \tan \alpha - \mu \right) \ .\]Le coefficient de frottement vaut \(\mu=0.15\). Sans résoudre l’équation précédente, déterminer la nature du mouvement pour \(\alpha = 5^{\circ}\) ; pour \(\alpha = 8.53^{\circ}\) ; pour \(\alpha = 11^{\circ}\).
4.3 Saut en chute libre (\(\ast\ast\) - 20~25min)
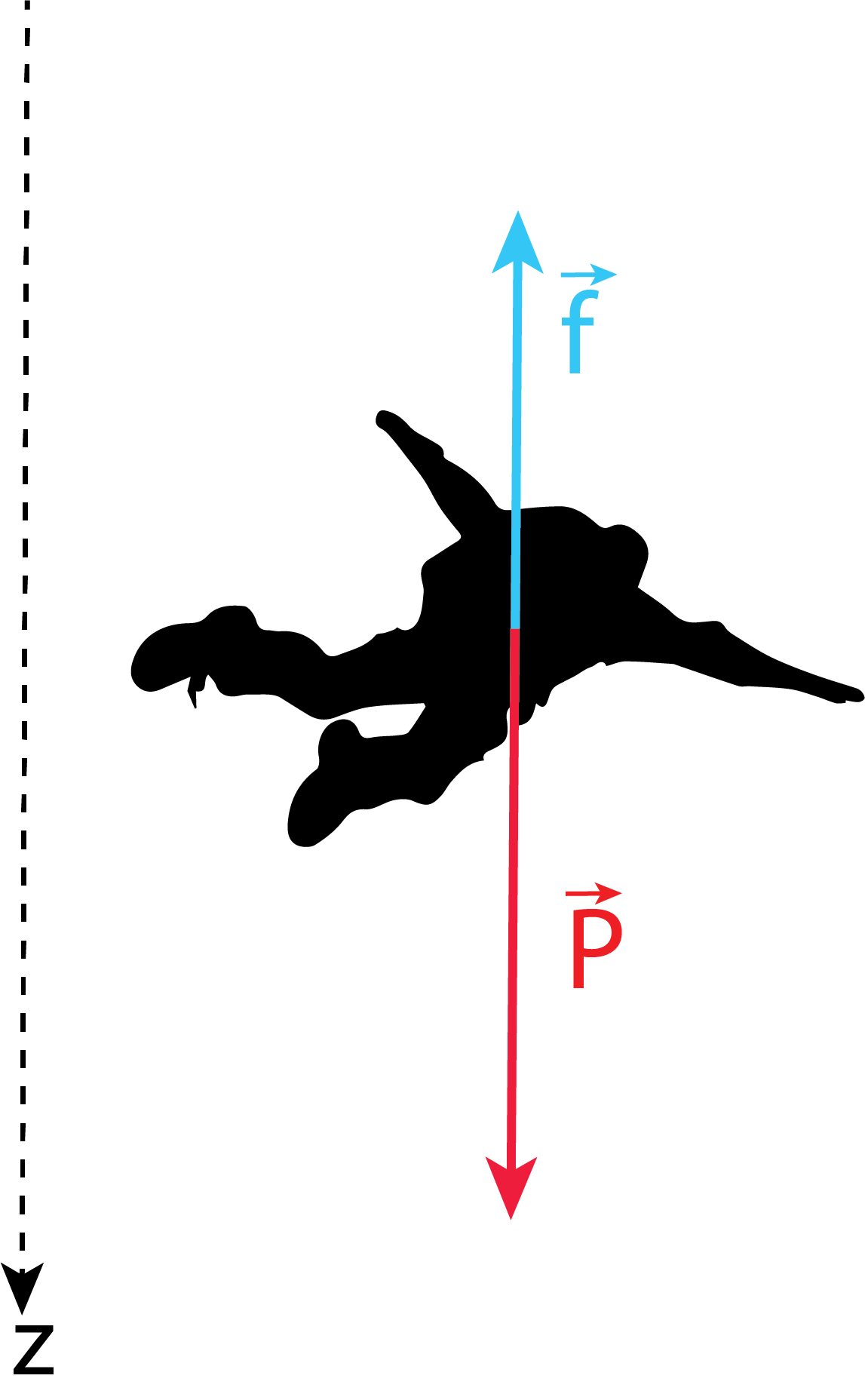
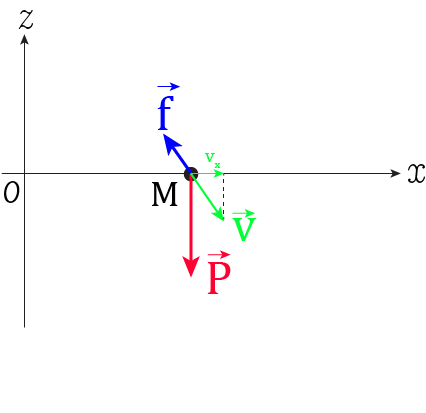
On étudie le mouvement d’un parachutisme de masse \(m\) en chute libre dans l’air. La résistance de l’air est modélisée par une force de frottement \(\vec{f}\) de norme \(\Vert \vec{f} \Vert = \frac{1}{2} C_x \rho Sv^2\), où \(\rho\) est la masse volumique de l’air, \(C_x\) le coefficient de traînée, et \(S\) la surface projetée (\(S=\pi a^2\) pour une sphère par exemple). On suppose que le parachutiste saute sans vitesse initiale. On se place dans un repère cartésien dont l’axe vertical \((Oz)\) est orienté vers le bas.
Définir le système et faire le bilan des forces.
Faire un schéma représentant le repère et les forces, dont on précisera les composantes.
En appliquant le principe fondamental de la dynamique, montrer que la composante selon \(z\) de la vitesse vérifie l’équation :
\[\frac{d v_z}{d t} = \alpha - \beta v_z^2 \ ,\]où \(\alpha\) et \(\beta\) sont deux constantes que l’on déterminera en fonction des données de l’énoncé.
À l’issue d’un régime transitoire, le parachutiste atteint la vitesse stationnaire \(v_{\infty}\). Déterminer l’expression de \(v_{\infty}\) en fonction de \(\alpha\) et \(\beta\).
Faire l’application numérique pour \(m=70\) kg, \(g=9,8~\text{m}\cdot \text{s}^{-2}\), \(\rho=1,3~\text{kg}\cdot \text{m}^{-3}\), et \(C_x=1\). On proposera une estimation de \(S\) selon que le parachutiste soit en position verticale ou horizontale.

Fig. 42 Formation de parachutistes pratiquant la chute libre.
4.4 Mouvement balistique en présence de frottement visqueux (\(\ast\ast\) - 15~20min)
Un projectile de masse \(m\) est lancé depuis le bord d’une falaise avec une vitesse initiale horizontale : \(\vec{v}_0=v_0 \vec{e}_x\). Le mouvement se déroule dans le plan \(Oxz\), l’axe vertical \(Oz\) étant orienté vers le haut. Le projectile, assimilé à un point matériel, est soumis à la force de frottement fluide \(\vec{f}=-k \vec{v}\), où \(k\) est une constante.
En appliquant le principe fondamental de la dynamique, établir l’équation vérifiée par la composante \(v_x\) de la vitesse. Montrer qu’elle peut se mettre sous la forme :
\[\frac{d v_x}{d t} = -\frac{1}{\tau} v_x (t) \ ,\]où \(\tau\) est une constante dont on déterminera la dimension.
On cherche une solution de la forme : \(v_x(t)= K e^{-\beta t}\). Injecter cette solution dans l’équation pour déterminer l’expression du paramètre \(\beta\).
À partir des conditions initiales, relier également la constante \(K\) aux données du problème.
Déterminer l’expression de la position \(x(t)\). Montrer qu’elle tend vers une valeur finie \(x_{\infty}\) lorsque \(t\to + \infty\). Tracer la courbe représentative de la fonction \(x(t)\).