6. Travail, puissance et énergie

Dans les chapitres précédents, nous avons analysé les mouvements à partir de la notion de force. Nous adoptons ici une description en terme d’énergie, qui est un concept central en physique. Nous introduisons d’abord les notions de travail et de puissance dans le cadre de la mécanique du point. Nous discutons ensuite les théorèmes qui sont déduits du principe fondamental de la dynamique.

Introduction

Prenons le cas de la chute libre : un objet de masse \(m\) est lâché sans vitesse initiale de l’altitude \(z=h\) au-dessus du sol. Nous avons vu au chapitre 3 que l’objet accélère sous l’effet de la gravité, de telle sorte que la vitesse au point d’impact (\(z=0\)) soit donnée par :

\[v = \sqrt{2gh} \ .\]

Or si on élève cette égalité au carré et que l’on multiplie par \(m/2\), on peut encore écrire :

\[\frac{1}{2}mv^2 = mgh \ .\]

On voit apparaître à gauche l’énergie cinétique \(E_c=\frac{1}{2}m v^2\), et à droite le travail du poids \(W=mgh\). Cette relation montre qu’il est possible d’analyser le phénomène de chute libre à partir d’un raisonnement qui traduit les transferts entre différentes formes d’énergie.

Travail et puissance d’une force

Définition du travail élémentaire

Considérons la situation représentée sur la ch6_travail: un point matériel \(M\) se déplace le long de la trajectoire \(\mathcal{C}\) sous l’action d’une force extérieur \(\vec{F}\). Entre deux instants infiniment voisins \(t\) et \(t+dt\), la position \(\vec{r}(t) = \overrightarrow{OM}\) du point matériel aura varié de la quantité infinitésimale \(d\vec{\ell} = \vec{r}(t+dt)-\vec{r}(t)\).

On définit alors le travail élémentaire de la force \(\vec{F}\) :

()\[\boxed{\delta W (\vec{F}) = \vec{F} \cdot d\vec{\ell} \ .}\]

L’unité SI du travail est le joule (J). À ce stade, nous pouvons déjà faire plusieurs remarques :

• la définition du travail élémentaire de l’équation () fait intervenir le produit scalaire de la force et du déplacement. En coordonnées cartésiennes, on a \(d\vec{\ell} = dx \, \vec{e_x}+dy \, \vec{e_y}+dz\, \vec{e_z}\), donc le travail élémentaire s’écrit encore : \(\delta W (\vec{F}) =F_x\, dx + F_y\, dy + F_z\, d z\).

• la notation — \(\delta W\) et non \(d W\) — est importante car nous verrons plus loin que le travail peut dépendre du chemin \(\mathcal{C}\) pour aller de \(A\) à \(B\).

• Le travail est additif : \(\delta W (\vec{F_1}+\vec{F_2}) = \delta W (\vec{F_1}) + \delta W (\vec{F_2})\).

Le travail élémentaire \(\delta W\) de la force \(\vec{F}\) est défini par : \(\delta W = \vec{F}\cdot d \vec{\ell}\).

Il est important de noter que le travail est une grandeur scalaire. Il est donc caractérisé par un signe dont l’interprétation physique est la suivante :

• Si \(\vec{F}\) et \(d \vec{\ell}\) sont dans le même sens, alors \(\delta W > 0\). Le travail élémentaire est dit moteur.

• Si \(\vec{F}\) et \(d \vec{\ell}\) sont de sens opposé, alors \(\delta W < 0\). Le travail élémentaire est dit résistif.

• Si \(\vec{F}\) est perpendiculaire à \(d \vec{\ell}\), alors \(\delta W = 0\). Dans ce cas, la force \(\vec{F}\) ne travaille pas.

Application 6.1: On considère le déplacement élémentaire d’un point matériel soumis uniquement à son poids. Discuter le signe de \(\delta W\) lorsque : (i) \(d\vec{\ell} = dz\, \vec{e}_z\), et (ii) \(d\vec{\ell} = dx\, \vec{e}_x\).

1. \(d\vec{\ell} = dz\, \vec{e}_z\)

Le déplacement est dans le même sens que le poids, donc \(\delta W > 0\) et le travail élémentaire est moteur.

2. \(d\vec{\ell} = dx\, \vec{e}_x\)

Le déplacement est perpendiculaire au poids, donc \(\delta W = 0\) et le poids ne travaille pas.

Puissance d’une force

Par définition, la puissance \(\mathcal{P}\) est donnée par le produit scalaire de la force \(\vec{F}\) et de la vitesse instantanée du point matériel :

()\[\boxed{\mathcal{P}= \vec{F} \cdot \vec{v} \ .}\]

L’unité SI de puissance est le Watt (W). La puissance est directement reliée au travail élémentaire (éq. ()). En effet, avec les notations introduites précédemment, on a \(\vec{v} = d \vec{\ell} / dt\) et donc :

()\[\delta W = \mathcal{P}d t \ .\]

En raison de la relation simple entre \(\mathcal{P}\) et \(\delta W\), les remarques faites sur le travail sont aussi valables pour la puissance. On peut également déduire la relation : \(1~\text{W}=1~\text{J}\cdot \text{s}^{-1}\).

Travail d’une force au cours d’un déplacement fini

Lors du déplacement du point matériel \(M\) le long de la trajectoire \(\mathcal{C}\) entre les points \(A\) et \(B\), le travail total de la force \(\vec{F}\) est donné par :

()\[\boxed{W_{A \rightarrow B}= \int_{\mathcal{C}} \delta W =\int_{ A}^{B} \vec{F} \cdot d \vec{\ell} \ .}\]

En langage mathématique, on dira que le travail correspond à la circulation du vecteur \(\vec{F}\). L’équation () implique en particulier que le travail total dépend explicitement du chemin \(\mathcal{C}\) suivi pour aller du points \(A\) au point \(B\).

En mathématique, on définit l’intégrale d’une fonction \(f(x)\) entre \(a\) et \(b\) comme la variation de la primitive de \(f(x)\) entre \(a\) et \(b\) :

\[\int_a^b f(x) dx = F(b) - F(a) \ ,\]

où \(\frac{d F}{dx}= f(x)\). Géométriquement, l’intégrale correspond à l’aire du domaine délimité par la courbe représentative de \(f(x)\).

En pratique, pour calculer un travail, on procédera de la façon suivante :

• on commence par déterminer les composantes de la force.

• on calcul le travail élémentaire \(\delta W=\vec{F} \cdot d \vec{\ell}\).

• on écrit explicitement l’intégrale () en prenant soin de bien spécifier les bornes d’intégration.

À titre d’illustration, nous discutons maintenant le travail des quelques forces usuelles.

Travail d’une force constante

Considérons pour fixer les idées le travail d’une force constante \(\vec{F}=F \vec{e}_x\) le long d’une trajectoire rectiligne horizontale, entre le point \(A\) de coordonnées \((x_A,0,0)\) et le point \(B\) de coordonnées \((x_B,0,0)\). Étant donné le déplacement \(d \vec{\ell}=dx \,\vec{e}_x\), le travail élémentaire de la force s’écrit :

\[\delta W = \vec{F} \cdot d \vec{\ell} = F \text{d}x \ .\]

On obtient alors le travail total :

()\[W_{A \rightarrow B} = \int_{x_A}^{x_B} F dx = F (x_B-x_A) \ .\]

Application 6.2: On pousse un carton le long d’une surface horizontale avec une force constante de norme 10 N, sur une distance de 5 m. Calculer le travail associé.

On applique l’équation ():

\[\begin{split}W &= \int_{0}^{5} F dx \\ &= \int_{0}^{5} 10 dx \\ &= 10 \int_{0}^{5} dx \\ &= 10 \times 5 = 50 J\end{split}\]

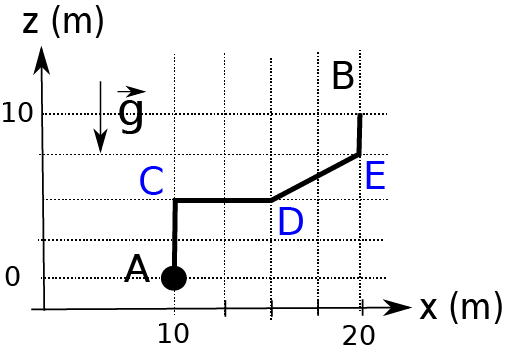
Travail du poids

Un exemple important de force constante est le poids : \(\vec{P}=m\vec{g}\). On suppose que l’axe \((Oz)\) est orienté vers le haut, de telle sorte que : \(\vec{g}= -g\vec{e}_z\). Nous allons exprimer le travail du poids le long d’un chemin \(\mathcal{C}\) reliant les points \(A(x_A,y_A,z_A)\) et \(B(x_B,y_B,z_B)\) — voir par exemple la ch6_travail_poids_exo.

Déplacement d’un point matériel selon un chemin allant de \(A\) à \(B\).

À 3 dimensions, l’expression du déplacement est : \(d \vec{\ell}=dx\, \vec{e_x}+dy\, \vec{e_y}+dz\, \vec{e_z}\). On a donc :

\[\delta W = \vec{P} \cdot d \vec{\ell} = -mgd z \ .\]

On remarque que les déplacements selon \(x\) et \(y\) ne contribuent pas au travail. Cela provient du fait que la force est entièrement dirigée selon \((Oz)\). Le travail total s’obtient alors en calculant l’intégrale :

()\[W_{A \to B} = \int_{\mathcal{C}} \vec{P} \cdot d \vec{\ell}=\int_{z_A}^{z_B} (-mg dz) = - m g (z_B - z_A) \ .\]

Ce dernier résultat montre que \(W_{A \to B} <0\) si \(z_B > z_A\) (resp. \(W_{A \to B} >0\) si \(z_B < z_A\)) : le travail est bien résistif lorsqu’on déplace la masse du bas vers le haut (resp. moteur dans la situation inverse).

Application 6.3: Une masse \(m=1\) kg est déplacée verticalement d’une hauteur de 10 m le long du chemin de \(A\) vers \(B\) représenté sur la ch6_travail_poids_exo . Calculer le travail du poids.

Déplacement d’un point matériel selon un chemin allant de \(A\) à \(B\).

On s’intéresse au travail du poids qui est orienté suivant l’axe \((Oz)\). Nous allons diviser le parcours en plusieurs étapes (notées C, D et E sur la ch6_travail_poids_exo2), et calculer le travail du poids sur chacune d’elle:

1. De A vers C:

   \[\begin{split}W_{A \to C} &= - m g (z_C - z_A) = -m g \times (5 - 0) \\ &= -5 m g\end{split}\]

2. de C vers D:

   \[\begin{split}W_{C \to D} &= - m g (z_D - z_C) = -m g \times (5 - 5)\\ &= 0 \\\end{split}\]

   on pouvait s’y attendre puisque entre C et D le poids est perpendiculaire au déplacement et donc ne travaille pas.

3. de D vers E:

   \[\begin{split}W_{D \to E} &= - m g (z_E - z_D) = -m g \times (7.5 - 5)\\ &= -2.5 m g \\\end{split}\]

4. de E vers B:

   \[\begin{split}W_{E \to B} &= - m g (z_B - z_E) = -m g \times (10 - 7.5)\\ &= -2.5 m g \\\end{split}\]

Soit finalement:

\[\begin{split}W_{A \to B} &= W_{A \to C} + W_{C \to D} + W_{D \to E} + W_{E \to B} \\ &= -5 mg +0 -2.5mg -2.5mg = -10mg\end{split}\]

On vérifie donc bien qu’on aurait pu directement écrire:

\[W_{A \to B} = -mg (z_B -z_A) = -10 mg\]

sans se préoccuper des étapes intermédiaires, puisque le poids ne travaille que pour les déplacements verticaux.

Travail d’une force de frottement fluide

On considère le mouvement d’un point matériel soumis à une force de frottement fluide \(\vec{f}=-k \vec{v}\), le long d’un chemin \(\mathcal{C}\) allant du point \(A\) à l’instant initial \(t_i\) au point \(B\) à l’instant final \(t_f\). Dans ce cas, il s’avère plus judicieux d’évaluer d’abord la puissance :

\[\mathcal{P} = \vec{f} \cdot \vec{v} = -k v(t)^2 \ .\]

La vitesse étant une fonction du temps, il en est de même pour la puissance. Le travail élémentaire s’écrit alors : \(\delta W = -k v(t)^2 dt\), de telle sorte que le travail total soit donné par :

\[W = -k \int_{t_i}^{t_f} v(t) ^2 dt \ .\]

Pour calculer cette dernière intégrale, il est nécessaire de connaître explicitement la fonction \(v(t)\) à chaque instant : autrement dit, le travail dépend de l’intégralité du chemin \(\mathcal{C}\) de \(A\) à \(B\). On note également que le travail est toujours résistif : \(W<0\).

Théorème de l’énergie cinétique

Nous appliquons maintenant les définitions du travail et de la puissance pour dériver plusieurs théorèmes importants en mécanique.

Définition de l’énergie cinétique

Considérons tout d’abord un point matériel \(M\) de masse \(m\), se déplaçant à la vitesse instantanée \(\vec{v}\). On appelle énergie cinétique la grandeur scalaire suivante :

()\[\boxed{E_c = \frac{1}{2} m v^2 \ ,}\]

où \(v = \Vert \vec{v} \Vert\). On peut noter que, par définition, l’énergie cinétique est toujours positive : \(E_c \geq 0\).

Théorème de la puissance et de l’énergie cinétique

Le concept d’énergie cinétique apparaît naturellement en lien avec le principe fondamental de la dynamique. En effet, prenons le produit scalaire avec la vitesse \(\vec{v}\) :

()\[\sum \vec{F}_{ext} \cdot \vec{v} = m \left( \frac{d \vec{v}}{dt} \cdot \vec{v} \right) \ .\]

On voit apparaître à gauche la puissance des forces extérieures : \(\mathcal{P}(\vec{F}_{ext}) = \vec{F}_{ext} \cdot \vec{v}\). En ce qui concerne le terme de droite, nous pouvons encore écrire [1] :

()\[m \left( \frac{d \vec{v}}{dt} \cdot \vec{v} \right) = \frac{1}{2} m \frac{d}{dt} \left( \vec{v} \cdot \vec{v} \right) = \frac{d}{dt} \left( \frac{1}{2} m v^2 \right) \ .\]

En comparant les équations () et  (), on obtient le premier théorème de ce chapitre :

Theoreme

1.1 Théorème de la puissance cinétique:

Dans un référentiel galiléen, la dérivée temporelle de l’énergie cinétique d’un point matériel est égale à la puissance des forces extérieures.

Ceci s’exprime sous la forme mathématique suivante :

()\[\boxed{\frac{ d E_c}{dt} = \sum \mathcal{P} (\vec{F}_{ext}) \ .}\]

Le Théorème de la puissance cinétique exprime une relation entre quantités instantanées : puissance et énergie cinétique. Or si on utilise la relation entre puissance et travail, \(\delta W = \mathcal{P}dt\), on obtient encore :

\[dE_c = \sum \mathcal{P} (\vec{F}_{ext})dt = \sum \delta W (\vec{F}_{ext}) \ .\]

En intégrant cette dernière égalité entre l’instant initial \(t_i\) et l’instant final \(t_f\), nous arrivons finalement au second théorème important :

Theoreme

1.2 Théorème de l’énergie cinétique:

Dans un référentiel galiléen, la variation de l’énergie cinétique d’un point matériel entre deux points est égale au travail des forces extérieures.

En termes mathématiques :

()\[\boxed{ \Delta E_c = E_c^{f} - E_c^{i} = \sum W (\vec{F}_{ext})}\]

Exemple d’application 1

Prenons l’exemple concret d’un skieur de masse \(m\), qui s’élance sans vitesse initiale sur un tremplin. On choisit pour cela un repère cartésien tel que l’axe \((Oz)\) soit orienté vers le haut, l’altitude \(z=0\) correspondant au bas du tremplin. On note \(h\) la différence d’altitude entre le haut et le bas du tremplin. On suppose que les forces de frottement sont négligeables.

• État initial : le skieur se situe à l’altitude \(z_i=h\), et sa vitesse est nulle : \(v_i=0\).

• État final : le skieur décolle du tremplin à l’altitude \(z_f=0\), et sa vitesse (inconnue) est \(v_f=v\).

• On applique le Théorème de l’énergie cinétique entre ces deux instants :

  \[\frac{1}{2} m v_f^2 - \frac{1}{2} mv_i^2 = -mg (z_f-z_i) \ ,\]

le travail du poids ayant déjà été calculé dans l’équation (). Étant donné que \(h=z_i-z_f\), on obtient ainsi directement la vitesse au moment où le skieur quitte le tremplin :

\[v=\sqrt{2gh} \ .\]

Application 6.4 Calculer la vitesse d’envol du skieur pour un tremplin de hauteur \(h=90\) m.

Application numérique:

\[v=\sqrt{2\times9.81\times90} = 34.3 \text{ m . s}^{-1}\]

Exemple d’application 2

Considérons comme deuxième exemple le mouvement d’une balle de masse \(m\) qui se déplace le long d’une surface horizontale. La vitesse initiale de la balle est \(v_0\). On souhaite calculer la distance \(D\) parcourue par la balle avant qu’elle ne s’arrête du fait des forces des frottement solide.

• Système : la balle, assimilée à un point matériel de masse \(m\).

• Repère cartésien \(Oxyz\), l’axe vertical \((Oz)\) étant orienté vers le haut. Le mouvement se déroulant entièrement selon \((Ox)\).

• Bilan des forces : poids \(\vec{P}=-mg\vec{e}_z\), réaction \(\vec{R}_n=R_n \vec{e}_z\), frottement solide \(\vec{R}_t=-R_t \vec{e}_x\).

L’équilibre des forces selon \(z\) (qui implique \(R_n=mg\)) associé à la loi de Coulomb (\(R_t=\mu R_n\)) détermine l’intensité de la force de frottement : \(R_t=\mu mg\). En appliquant le Théorème de l’énergie cinétique entre l’instant inital (\(x=0\), \(v=v_0\)) et l’instant final (\(x=D\), \(v=0)\), on obtient :

\[-\frac{1}{2}mv_0^2 = -\int_{0}^D R_t dx = -\mu mgD \quad \Rightarrow \quad D = \frac{v_0^2}{2\mu g} \ .\]

Application 6.5: Calculer la distance d’arrêt de la balle pour \(v_0=5~\text{m}\cdot\text{s}^{-1}\) et \(\mu=0.5\)

Application numérique:

\[D = \frac{v_0^2}{2\mu g} =\frac{5^2}{2\times 0.5\times 9.81}=2.55\text{ m}\]

Énergie potentielle

Jusqu’à présent, nous avons introduit deux formes d’énergie : le travail d’une force \(W\) et l’énergie cinétique \(E_c\). Nous définissons maintenant l’énergie potentielle à partir de la notion de force conservative.

Force conservative

En général, le travail d’une force entre deux points \(A\) et \(B\) dépend du chemin \(\mathcal{C}\) suivi pour aller de \(A\) à \(B\). C’est typiquement le cas pour les forces de frottements. Il existe cependant des forces pour lesquelles le travail dépend uniquement du point initial et du point final : par exemple, le travail du poids entre \(A\) et \(B\) est donné par \(W=-mg(z_B-z_A)\), indépendamment de la façon dont on va d’un point à l’autre.

Definitions

1.3 Définition. Une force \(\vec{F}\) dont le travail entre deux points ne dépend pas du chemin parcouru est dite conservative. Dans le cas contraire, elle est non conservative.

Les forces de frottements sont un exemple de force non conservatives. Nous nous concentrons dans la suite sur le cas des forces conservatives.

Définition de l’énergie potentielle

Si la force \(\vec{F}^c\) conservative, alors le travail entre un point initial et un point final ne dépend que de ces deux points. On peut donc écrire :

()\[\boxed{ W (\vec{F}^c)= -\Delta E_p \ , \quad \text{avec} \quad \Delta E_p = E_p^f - E_p^i \ .}\]

\(E_p\) représente l’énergie potentielle associée à la force conservative \(\vec{F}^c\). La relation () s’exprime également sous forme infinitésimale :

()\[\boxed{ \delta W (\vec{F}^c)= -d E_p \ .}\]

Exemples d’énergies potentielles

Énergie potentiel de pesanteur

Si l’axe \((Oz)\) est orienté vers le haut, le travail élémentaire du poids \(\vec{P} = m\vec{g}\) est donné par :

\[\delta W = \vec{P} \cdot d \vec{\ell} = -mg dz \ .\]

Nous pouvons donc écrire \(d E_p = mg dz\), soit encore après intégration :

\[\boxed{E_p(z) = mg z + C \ ,}\]

où \(C\) est une constante. On voit sur ce premier exemple que l’énergie potentielle est définie à une constante près.

Énergie potentielle d’un ressort

Nous avons vu au chapitre 4 que la force de rappel élastique d’un ressort horizontal de raideur \(k\) et de longueur à vide \(x_0\) est donnée par : \(\vec{F} = -k (x - x_0) \vec{e_x}\). Le travail élémentaire est donc :

\[\delta W = \vec{F} \cdot d \vec{\ell} = -k(x-x_0) dx= -dE_p\]

Le travail élémentaire est donc : \(\delta W = \vec{F} \cdot d \vec{\ell} = -k(x-x_0) dx= -dE_p\). Cette dernière égalité peut encore s’écrire : \(\frac{dE_p}{dx} = k (x - x_0)\), de telle sorte que l’énergie potentielle élastique soit donnée par :

()\[\boxed{ E_p = \frac{1}{2}k (x-x_0)^2+ C \ .}\]

La constante peut être fixée en imposant par exemple la condition \(E_p(x_0)=0\), auquel cas on obtient encore : \(E_p = \frac{1}{2}k (x-x_0)^2\). L’énergie potentielle élastique varie donc comme le carré de l’allongement du ressort.

Énergie potentielle de gravitation

Considérons la situation représentée sur la ch6_grav: deux points matériels, de masse respective \(m_1\) et \(m_2\), sont séparés de la distance \(r\). On suppose que l’origine \(O\) des coordonnées coïncide avec la position du point de masse \(m_1\). La position du point \(M\) de masse \(m_2\) est repérée par \(\vec{r}=\overrightarrow{OM}\). La force d’attraction gravitationnelle entre les deux points matériels est donnée par :

()\[\vec{F}_{1\to 2} = - \mathcal{G} \frac{m_1 m_2}{r^2}\vec{u} \ ,\]

où \(\vec{u}=\vec{r}/ r\) est le vecteur unitaire de la droite \((OM)\).

Interaction gravitationnelle entre deux points matériels séparés de la distance \(r\).

Concentrons-nous tout d’abord sur le travail élémentaire \(\delta W = \vec{F}_{1\to 2} \cdot d \vec{\ell}\) associé au déplacement infinitésimal \(d \vec{\ell}\). Étant donné que seule la composante selon \(\vec{u}\) de \(d \vec{\ell}\) contribue au travail, on peut écrire \(d \vec{\ell} = d r \, \vec{u}\), où \(dr\) est la variation infinitésimale de la distance séparant les deux points. On a alors :

\[\delta W = - \mathcal{G} \frac{m_1 m_2}{r^2} dr = -d E_p \ , \quad \text{soit encore:} \quad \frac{d E_p}{dr} = \mathcal{G} \frac{m_1 m_2}{r^2} \ .\]

On obtient donc finalement :

()\[\boxed{E_p(r) = -\mathcal{G} \frac{m_1 m_2}{r} + C \ .}\]

Encore une fois, on trouve que l’énergie potentielle est définie à une constante près. Cette dernière peut être fixée en supposant par exemple que l’énergie est nulle lorsque les deux points sont infiniment loin l’un de l’autre :

\[\lim_{r\to \infty} E_p(r) = 0 \quad \Rightarrow \quad C=0 \ .\]

Théorème de l’énergie mécanique

Nous avons vu au §:ref:sec_epot qu’il existe deux types de forces : les forces conservatives \(\vec{F}^c\), qui dérivent d’une énergie potentielle, et les forces non conservatives \(\vec{F}^{nc}\), dont la travail dépend du chemin suivi. Cette distinction va prendre tout son sens avec la notion d’énergie mécanique.

Énergie mécanique

Definitions

1.4 Définition. On appelle énergie mécanique \(E_m\) d’un point matériel la somme de son énergie cinétique et son énergie potentielle : \(E_m = E_c +E_p\).

L’énergie mécanique joue un rôle central en physique car elle est reliée aux échanges entre les différentes formes d’énergie.

---

Réécrivons le Théorème de l’énergie cinétique en prenant soin de distinguer les forces conservatives et non conservatives :

\[\Delta E_c =E_c^f - E_c^i = W(\vec{F}^c) + W(\vec{F}^{nc}) \ .\]

Or d’après la relation (), on a : \(W(\vec{F}^c) = - \Delta E_p\). En regroupant les énergies cinétiques et potentielles, on obtient finalement le résultat suivant :

Theoreme

1.5 Théorème de l’énergie mécanique

La variation de l’énergie mécanique est égale au travail des forces non conservatives.

Sous forme mathématique, on a donc :

()\[\boxed{\Delta E_m = E_m^f-E_m^i = W(\vec{F}^{nc}) \ .}\]

Cette formule signifie qu’en présence de forces non conservatives, le travail mécanique se transforme en une autre forme d’énergie (chaleur en particulier).

Conservation de l’énergie mécanique

Une conséquence immédiate du Théorème de l’énergie mécanique est que, si le système n’est soumis qu’à des forces conservatives, alors l’energie mécanique est constante :

()\[\boxed{W(\vec{F}^{nc})= 0 \quad \Rightarrow \quad E_m=E_p+E_c = C^{ste} \ .}\]

La conservation de l’énergie mécanique peut également être vraie en présence de forces non conservatives, dans le cas où ces dernières ne travaillent pas.

Représentation diagrammatique des transferts d’énergie

Revenons sur les différentes formes d’énergie que nous avons définies jusqu’ici, et qui peuvent être interprétées de la façon suivante :

• l’énergie cinétique \(E_c\) est l’énergie que possède un corps du fait de son mouvement. Elle est nulle si le système est au repos (\(v=0\)).

• l’énergie potentielle \(E_p\) est l’énergie emmagasinée par le système. Cette énergie peut être restituée au cours du mouvement.

• l’énergie mécanique \(E_m\) est la somme des deux contributions précédentes. Si les forces sont conservatives, \(E_c\) et \(E_p\) varient au cours du mouvement mais \(E_m\) reste constante.

Les transferts entre énergie cinétique et potentielle peuvent être illustrés à l’aide d’un diagramme d’énergie. Considérons par exemple un point matériel de masse \(m\) qui est lancé vers le haut. La ch6_travail_energie_diag montre l’évolution de la trajectoire à 5 instants différents. L’objet étant soumis uniquement à son poids, l’énergie mécanique est conservée : \(E_m (1)=E_m (2)=\ldots=E_m (5)=E_m\) (pointillés rouges sur la ch6_travail_energie_diag. Pour représenter les énergies cinétiques et potentielles, on fait alors appel à des histogrammes.

Diagrammes d’énergie dans le cas de la chute libre.

1. A l’instant \(t_1\), l’objet est lancé depuis l’altitude \(z=0\) à la vitesse \(v_1\). L’énergie potentielle étant nulle [2], on a : \(E_m= E_c (1)=\frac{1}{2}mv_1^2\).

2. A l’instant \(t_2\), l’objet est en phase d’ascension. La somme de l’énergie potentielle et de l’énergie cinétique est égale à l’énergie mécanique totale : \(E_m = E_c (2)+ E_p (2)\). La hauteur de la colonne pour l’énergie cinétique est égale à la partie manquante (en pointillés) dans l’énergie potentielle pour atteindre l’énergie mécanique totale.

3. A l’instant \(t_3\), l’objet a atteint son altitude maximale. Sa vitesse étant nulle, on a maintenant : \(E_c (3)=0\). L’énergie totale est donc uniquement de l’énergie potentiel : \(E_m = E_p (3)\).

4. A l’instant \(t_4\), l’objet est en phase descendante. La somme de l’énergie potentielle et de l’énergie cinétique est égale à l’énergie mécanique totale : \(E_m = E_c (4)+ E_p (4)\). Ce cas est similaire au cas 2.

5. A l’instant \(t_5\), l’objet retombe sur le sol et son énergie potentielle est nulle : \(E_m =E_c(5)\).

Approche énergétique de la chute libre

Pour être complet, nous reprenons dans cette partie l’exemple de la chute libre discuté au chapitre 3, mais en suivant cette fois une approche énergétique. L’intérêt majeur de cette approche est qu’elle ne fait intervenir aucun vecteur, ce qui permet d’éviter certaines erreurs de projection.

On suppose que le point matériel est lâché à l’instant \(t=0\) sans vitesse initiale depuis l’altitude \(h\). Ceci correspond aux conditions initiales : \(z(0)=h\) et \(v(0)=0\). Pour trouver les équations du mouvement, écrivons l’expression des énergies cinétiques et potentielles à un instant quelconque \(t\) :

\[E_c(t) = \frac{1}{2} m v^2 (t) \ , \quad \text{et} \quad E_p(t)= mgz(t) \ .\]

La conservation de l’énergie mécanique \(E_m(t)=E_m(0)=E_m\) implique alors :

()\[E_m= \frac{1}{2} m v^2 (t) + mgz(t) = mg h \ .\]

On détermine en particulier la vitesse \(v_f\) lorsque l’objet atteint le sol (\(z=0\)) :

\[E_m= \frac{1}{2} m v_f^2 =mg h \quad \Rightarrow \quad v_f =\sqrt{2 gh} \ .\]

Pour connaître la vitesse à chaque instant, il suffit de dériver l’équation () par rapport au temps :

\[mv \frac{dv}{dt} + mg \frac{dz}{dt} =0 \ .\]

En notant que \(dz/dt = v\), on obtient après simplification :

\[\frac{dv}{dt}=-g \quad \Rightarrow \quad \boxed{v(t)=-gt \ .}\]

On retrouve ainsi les équations obtenues à partir du principe fondamental de la dynamique.

[1]

Un produit scalaire se dérive comme un produit ordinaire de deux fonctions.

[2]

On choisit comme référence l’énergie potentielle au niveau du sol : \(E_p(z=0)=0\).