Nous appliquons maintenant les lois de Newton pour décrire la dynamique
des points matériels. Les forces que nous discutons dans ce chapitre
sont des forces de contact : frottement, tension, réaction, et force
élastique.
Commençons par résumer la méthodologie que l’on adoptera
systématiquement pour déterminer les propriétés du mouvement d’un
point matériel.
Définition du système : quel est le système étudié ? Cette question est importante quand on étudie un ensemble de points matériels en interaction (système planète-satellite par exemple).
Schéma et définition du repère : le schéma constitue une aide précieuse au moment de projeter les forces sur les axes du repère.
Bilan des forces : cette étape essentielle consiste à recenser l’ensemble des forces qui s’appliquent au système, quitte éventuellement à en négliger certaines par la suite.
Principe fondamental de la dynamique : on écrit d’abord l’égalité vectorielle, que l’on projette ensuite pour obtenir les équations différentielles du mouvement.
Résolution des équations du mouvement : on intègre les équations différentielles en tenant compte des conditions initiales pour la vitesse et la position.
Au final, ce raisonnement permet d’obtenir les équations horaires du
mouvement, c’est-à-dire les fonctions \(x(t)\), \(y(t)\) et
\(z(t)\). On peut ensuite déterminer toutes les quantités physiques
pertinentes (énergie, fréquence d’un mouvement périodique, …).
Avertissement
On retiendra surtout qu’il est capital de ne négliger aucune de ces
étapes, qui sont chacune importantes lors de la résolution d’un
problème en mécanique du point. Dans la suite, nous appliquons cette
méthodologie à différentes forces que l’on rencontre couramment en
physique.
Lorsque l’on impose une contrainte de traction ou de compression à un
solide, la déformation qui en résulte varie linéairement avec la
contrainte. Cette loi, énoncée par le physicien anglais Robert Hooke (1635–1703), s’applique à de nombreux systèmes physiques à conditions
que la déformation ne soit pas trop grande.
Un ressort constitue un exemple simple de solide élastique. Supposons
comme représenté sur la figure fig-ch4_ressort-01 que l’une des
extrémités du ressort est fixée à l’origine \(O\), l’autre extrémité
dur ressort étant repérée par le point \(M\). On note
\(\vec{r} = \overrightarrow{OM}\) le vecteur position. En l’absence de
contrainte, le ressort a une longueur à vide
\(l_0= \Vert \vec{r}_0 \Vert\). Dès lors que l’on l’écarte le
ressort de la position au repos \(\vec{r}_0\), celui-ci exerce une
force de rappel élastique :
\[\vec{F} = - k \left( \vec{r}- \vec{r}_0 \right) \ ,\]
où \(k\) est la constante de raideur (unité :
\(\text{N} \cdot \text{m}^{-1}\)). Dans le cas unidimensionnel
représenté sur la fig-ch4_ressort-01, on a :
\(\vec{F} = - k \left( z- l_0 \right)\vec{e}_z\). On voit donc que
la force est dirigée de bas en haut si \(z>l_0\), et de haut en bas
si \(z<l_0\). Autrement dit, la force de rappel a toujours tendance
à ramener le ressort vers sa position au repos \(z=l_0\).
Considérons la situation où un point matériel de masse \(m\) est
accroché à l’extrémité du ressort (fig-ch4_ressort-01). Nous appliquons les lois de Newton
pour déterminer l’allongement du ressort en fonction de \(m\).
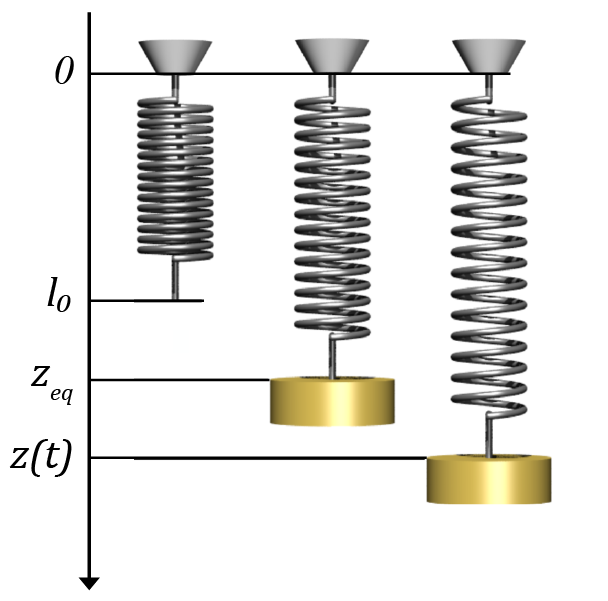
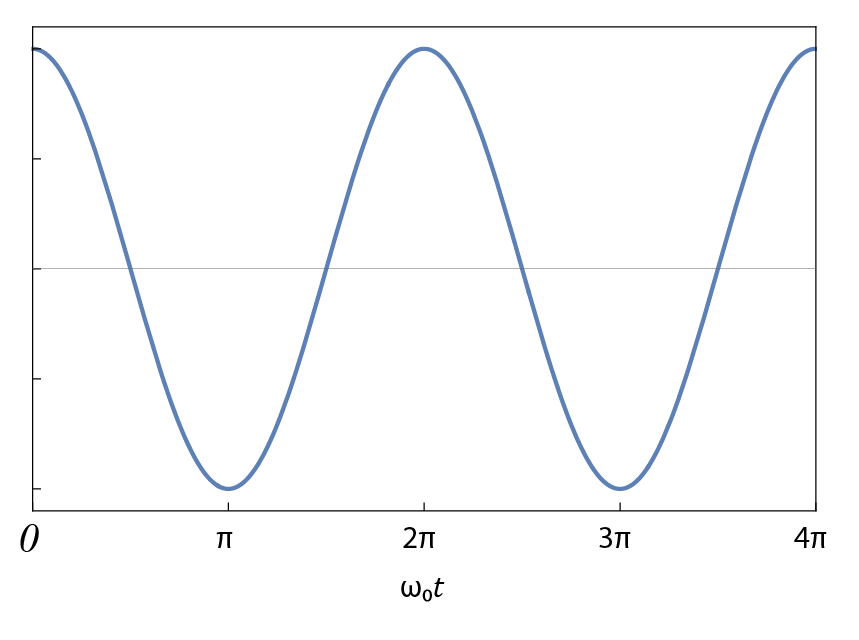
Fig. (a) La réponse mécanique d’un ressort vérifie la loi de Hooke. (b) Évolution de l’écart à l’équilibre \(u(t)\) en fonction du temps (variables adimensionnées).
Système : point matériel \(M\) de masse \(m\)
Repère cartésien \(Oxyz\), l’axe horizontal \((Oz)\) étant vertical, orienté vers le bas.
Bilan des forces :
le poids \(\vec{P}=m\vec{g}\)
la force de rappel \(\vec{F}=-k(\vec{r}-\vec{r}_0)\)
Principe fondamental de la dynamique : \(\vec{P}+ \vec{F} =m\vec{a}\)
Équations du mouvement: lorsque le système est à l’équilibre mécanique, on a \(\vec{a}=0\), et donc \(\vec{P}+ \vec{F} =\vec{0}\). En projetant sur l’axe \(Oz\), on trouve :
On écarte maintenant le ressort de sa position d’équilibre
\(z_{\textrm{eq}}\) (fig-ch4_ressort-01). En projetant le principe fondamental
de la dynamique sur l’axe \((Oz)\), on obtient l’équation
d’évolution pour la position \(z(t)\) du point matériel :
Le problème se simplifie si l’on considère l’écart
\(u(t) = z(t)-z_{\textrm{eq}}\) par rapport à la position
d’équilibre. Pour cela, on retranche l’équation () (qui vaut 0) de
l’équation () et l’on trouve :
\[\begin{split}m g - k(z-l_{0}) - \underbrace{\big( mg-k (z_{\textrm{eq}}-l_0) \big)}_{=0} = \parderder{z}{t} \\
\Leftrightarrow k(z_{\textrm{eq}}-z)= m \parderder{z}{t}\end{split}\]
or: \(\parderder{u}{t}=\parderder{z}{t}\) et donc:
On obtient ainsi l’équation différentielle d’un oscillateur
harmonique. On peut vérifier que la solution générale est donnée par :
\[u(t) = A \cos \omega_0 t +B \sin \omega_0 t \ ,\]
où \(A\) et \(B\) sont deux constantes d’intégration. Si l’on
suppose de plus que le ressort est lâché sans vitesse initiale, avec
\(u(0)= u_0\) l’écart inital, on trouve finalement :
La solution () est représentée sur la fig-ch4_ressort-02.
Application 4.1: Montrer que la fonction \(u(t) = A \cos \omega_0 t +B \sin \omega_0 t\) est bien solution de l’équation différentielle () . Déterminer les constantes d’intégration \(A\) et \(B\) correspondant aux conditions initiales : \(u(0)=u_0\) et \(\frac{d u}{dt} (0) = 0\). Tracer la courbe de \(u(t)\).
On considère l’équation différentielle suivante: \(\parderder{u}{t} + \omega_{0}^2 u=0\).
Vérifions que la fonction \(u(t)=A\cos{\omega_{0}t} + B \sin{\omega_{0} t}\) est bien solution:
\[\begin{split}\parder{u}{t} &= - A \omega_{0} \sin{\omega_0 t} + B \omega_{0} \cos{\omega_0 t} \\
\parderder{u}{t} &= - A \omega_{0}^2 \cos{\omega_0 t} - B \omega_{0}^2 \sin{\omega_0 t} \\\end{split}\]
et donc:
\[\begin{split}\parderder{u}{t} + \omega_{0}^2 u &= \underbrace{- A \omega_{0}^2 \cos{\omega_0 t} - B \omega_{0}^2 \sin{\omega_0 t}}_{\parderder{u}{t}} + \omega_{0}^2 \Big( \underbrace{A\cos{\omega_{0}t} + B \sin{\omega_{0} t}}_{u(t)} \Big) \\
&= - A \omega_{0}^2 \cos{\omega_0 t} - B \omega_{0}^2 \sin{\omega_0 t} + A \omega_{0}^2 \cos{\omega_0 t} + B \omega_{0}^2 \sin{\omega_0 t}
&= 0\end{split}\]
Les conditions initiales \(u(0)=u_0\) et \(\frac{d u}{dt} (0) = 0\) s’écrivent:
\[\begin{split}u(0) &=A \underbrace{\cos{\omega_0 \times 0}}_{=1} + B \underbrace{\sin{\omega_{0} \times 0}}_{=0} = A = u_{0} \\
\parder{u}{t}(0) &= - A \omega_{0} \underbrace{\sin{\omega_0 \times 0}}_{=0} + B \omega_{0} \underbrace{\cos{\omega_0 \times 0}}_{=1} = B \omega_{0} = 0\end{split}\]
d’où : \(A=u_{0}\) et \(B=0\) et finalement:
\(\boxed{u(t)=u_{0} \cos{\omega_{0} t}}\)
Évolution de l’écart à l’équilibre \(u(t)\) en fonction du temps (variables adimensionnées).
Applications
En calibrant la constante de raideur du ressort, on peut utiliser un ressort pour mesurer des masses. C’est sur ce principe que fonctionnent beaucoup de balance usuelles (balance de cuisine, ou de bagages)
Considérons un corps en contact avec une surface solide — un livre posé
sur une table par exemple. Si le corps n’était soumis qu’à la seule
force pesante \(\vec{P}\), il serait en chute libre. Pour rétablir
l’équilibre mécanique, il faut donc que le support exerce une force en
retour afin de compenser le poids. Il s’agit de la force de
réaction\(\vec{R}_n\), dont les caractéristiques sont les
suivantes :
son point d’application est le point de contact entre le système et le support.
elle est perpendiculaire au support, et orienté du support vers le système.
son intensité découle du principe fondamental de la dynamique.
Il est important de noter que l’intensité de cette force n’est pas
constante : elle s’adapte aux autres forces auxquelles est soumis le
système. Dans l’exemple de la fig-ch4_reaction (a), la
force de réaction est de même direction et même norme que le poids, mais
de sens opposé.
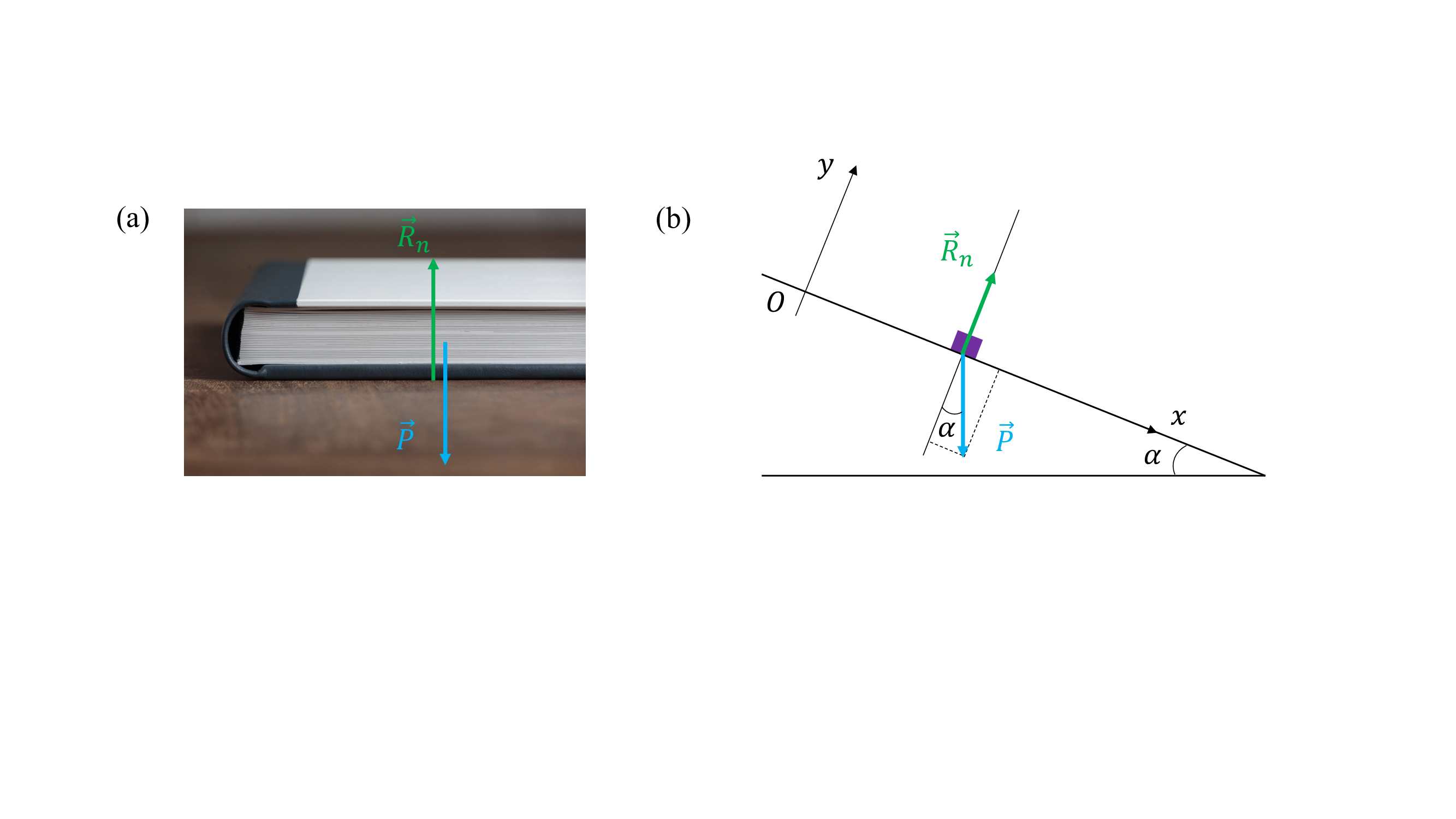
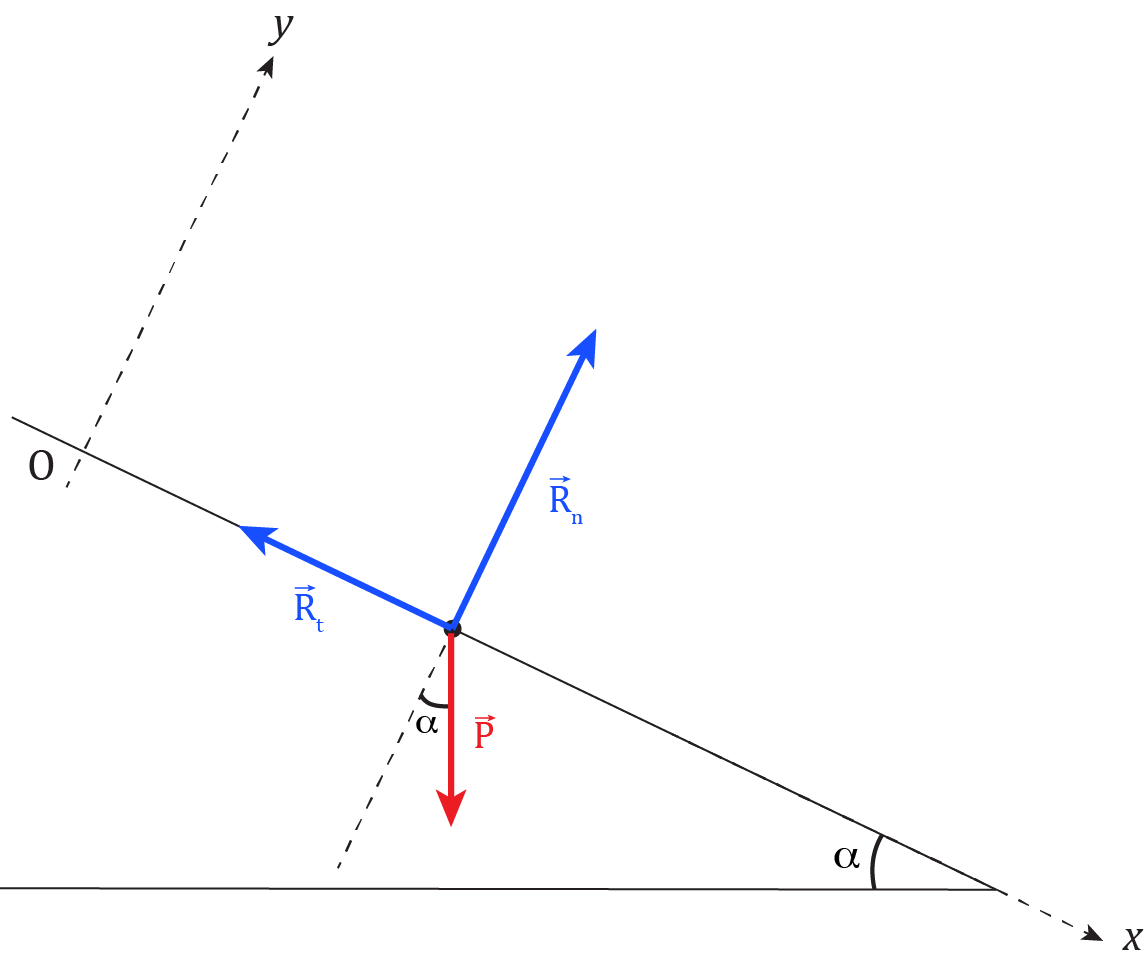
(a) À l’équilibre, la réaction \(\vec{R}_n\) du support compense
exactement le poids \(\vec{P}\). (b) Si la surface est inclinée,
le mouvement du solide assimilé à un point matériel est décrit par
les équations () et ().
À titre d’illustration, étudions le mouvement d’un corps assimilé à un
point matériel le long d’un support incliné d’un angle \(\alpha\)
par rapport à l’horizontale. Cette situation est représentée sur la fig-ch4_reaction (b).
Système : point matériel \(M\) de masse \(m\)
Repère cartésien \(Oxy\), le point \(O\) correspondant à la position initiale du point matériel. L’axe \((Ox)\) est confondu avec le support et est orienté vers le bas.
Bilan des forces :
le poids \(\vec{P}=m\vec{g}\)
la réaction du support \(\vec{R}_n\)
les forces de frottement sont négligées
Principe fondamental de la dynamique :
\(\vec{P}+\vec{R}_n=m\vec{a}\)
Cette égalité vectorielle est ensuite projetée sur les axes du repère.
On commence par déterminer les composantes des forces :
où \(R_n=\Vert \vec{R}_n \Vert\). On voit sur cet exemple qu’il
est absolument indispensable de faire un schéma lorsque l’on projette
les forces. On sera particulièrement vigilant quant au signe des
composantes (\(+\) ou \(-\) selon que la force soit dans le même
sens que le vecteur de base ou en sens opposé). On peut également
vérifier pour \(\alpha=0\) que l’on retrouve bien :
\(\vec{P}=-mg \vec{e}_y\).
Le principe fondamental de la dynamique conduit donc à un système
d’équations différentielles :
()\[m \displaystyle{\frac{d^2 x}{ d t^2}} = mg\sin \alpha\]
()\[m \displaystyle{\frac{d^2 y}{ d t^2}} = -mg\cos \alpha + R_n\]
Le point matériel étant en permanence en contact avec le support, on a
par définition : \(y(t)=0\), et par conséquent :
\(d y/ dt=d^2 y/ dt^2=0\). L’équation () permet
donc de déterminer l’intensité de la force de réaction :
\(R_n= mg \cos \alpha\). L’équation () décrit
quant à elle à un mouvement uniformément accéléré dans le champ de
pesanteur « effectif » \(g_{\textrm{eff}}=g\sin \alpha\).
Application 4.2: Intégrer l’équation () pour déterminer l’équation horaire \(x(t)\), en tenant compte des conditions initiales : \(x(0)=0\) et \(v_x(0)=0\).
Équation du mouvement: \(\parderder{u}{t} = g \sin{\alpha}\)
donc: \(v_{x}=\parder{x}{t}=g t \sin{\alpha} + C\)
Or \(v_x(0)=C=0 \Rightarrow \boxed{v_{x}(t)=g t \sin{\alpha}}\)
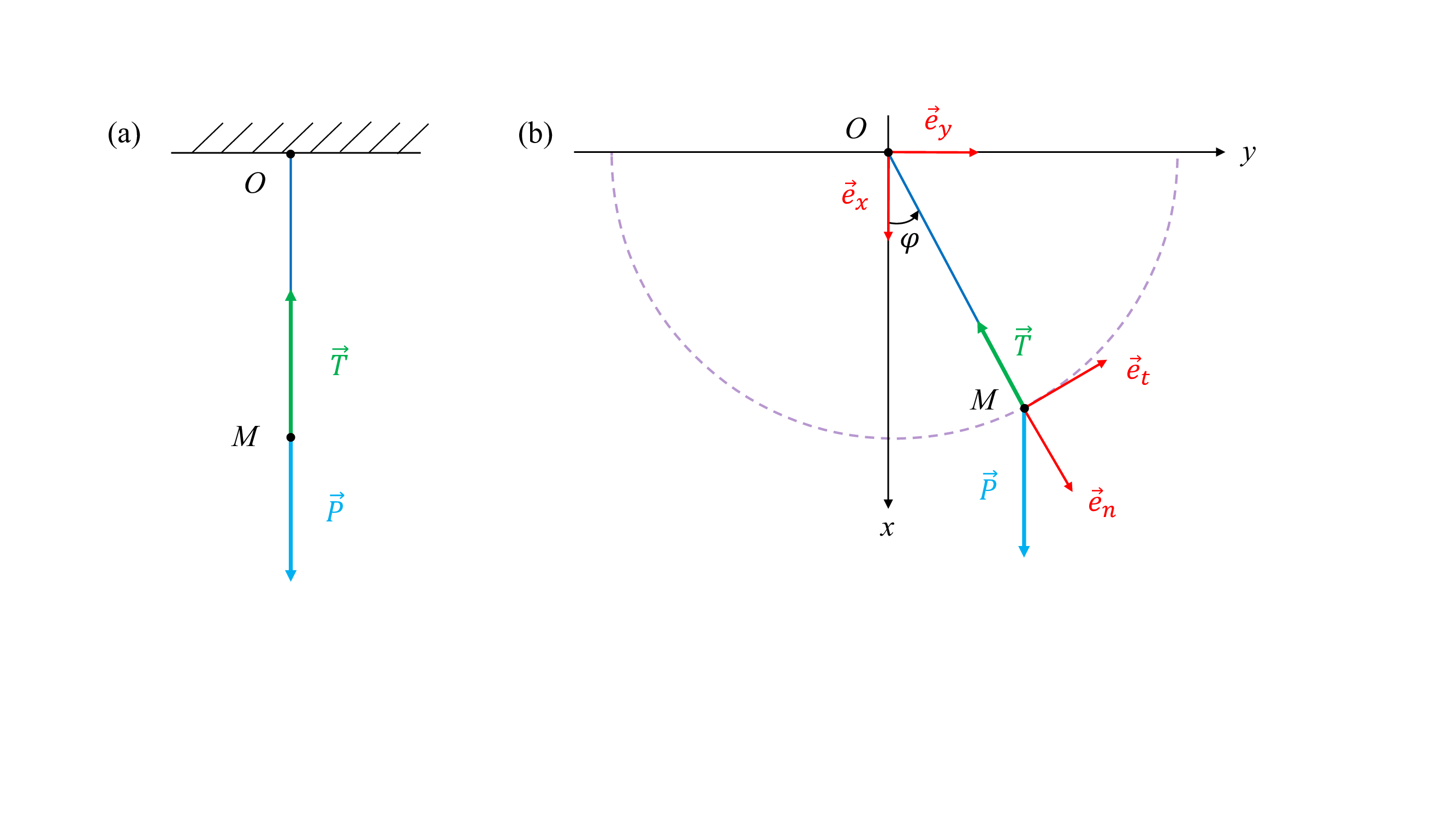
(a) À l’équilibre mécanique, la tension \(\vec{T}\) du fil vient
compenser le poids \(\vec{P}\) du point matériel \(M\). (b)
Lorsque l’on écarte le pendule de sa position d’équilibre, on obtient
une réalisation de l’oscillateur harmonique.
Une troisième force de contact usuelle est la force de tension, qui agit
lorsqu’un un point matériel \(M\) de masse \(m\) est accroché à
l’extrémité d’un fil inextensible (c’est-à-dire dont la longueur
\(\ell\) est constante). Comme pour la force de réaction, le point
matériel serait en chute libre s’il n’était soumis qu’à son seul poids —
voir la fig-ch4_tension (a). Pour rétablir l’équilibre
mécanique, on introduit la force de tension\(\vec{T}\) dont les
caractéristiques sont les suivantes :
direction : la droite définie par le fil.
sens : orientée du point matériel vers le fil.
norme : résulte du principe fondamental de la dynamique.
Encore une fois, l’intensité de la force n’est pas constante mais elle
s’adapte aux autres forces auxquelles est soumis le système.
Application
Oscillations d’un pendule
Supposons que l’on écarte le point matériel \(M\) de sa position
d’équilibre tout en maintenant le fil en tension. L’autre extrémité du
fil est accroché au point fixe \(O\), que l’on choisit comme origine
du repère \(Oxy\) représenté sur la
fig-ch4_tension (b). On note \(\varphi\) l’angle avec
l’axe vertical.
Système : point matériel de masse \(m\)
Repère : base locale \((\vec{e}_n,\vec{e}_t)\)
Bilan des forces :
le poids \(\vec{P}=m\vec{g}\)
la tension du fil \(\vec{T}\)
Principe fondamentale de la dynamique :
\(\vec{P}+\vec{T}=m\vec{a}\)
Commençons par déterminer les composantes des forces :
()\[m\ell \displaystyle{\frac{d^2 \varphi}{ d t^2}} = -mg\sin \varphi\]
L’équation () fait intervenir la tension \(T\) du
fil, qui n’est pas connue pour l’instant. Concentrons-nous plutôt sur la
seconde équation que l’on peut réécrire sous la forme :
Cette équation étant non-linéaire, sa résolution mathématique est
complexe. Néanmoins, pour des angles « pas trop grands », on peut
remplacer la fonction sinus par l’équation de sa tangente au voisinage
de 0 : \(\sin x \approx x\) (où \(x\) est exprimé en
radians). En pratique, cette approximation est valide pour des angles
inférieurs à \(30^{\circ}\). On obtient alors :
On reconnaît ici l’équation de l’oscillateur harmonique. Si l’on suppose
que le pendule est lâché de l’angle \(\varphi_0\) sans vitesse
initiale, on trouve finalement :
()\[\boxed{\varphi(t) = \varphi_0 \cos \omega_0 t \ .}\]
La période des oscillations du pendule est alors donnée par :
\[T= 2\pi \sqrt{\ell/g} \ .\]
Nous déterminons ainsi le préfacteur de la loi obtenue dans l’équation (1) au Chapitre 1 par analyse dimensionnelle.
Les notions de travail et d’énergie seront abordées en détail au
Chapitre 6. Néanmoins, nous anticipons cette discussion en notant que
les forces rencontrées jusqu’à présent sont conservatives : elles
sont telles que l’énergie totale ne varie pas au cours du mouvement. Or
on comprend bien que dans la plupart des situations réelles, l’énergie
n’est pas forcément constante. Nous décrivons dans cette dernière
section des forces non conservatives : les forces de frottement.
Reprenons la situation décrite sur la
fig-ch4_reaction (b): un corps, assimilé à un point
matériel de masse \(m\), se déplace le long d’une surface solide. La
force de réaction comporte généralement, outre la composante normale
\(\vec{R}_n\), une composante qui est parallèle au support : il
s’agit de la force de frottement solide que l’on notera
\(\vec{R}_t\). Cette force trouve son origine microscopique dans la
dissipation d’énergie au niveau des contacts entre le corps et la
surface.
Lorsque le corps est en mouvement, la force de frottement s’oppose au
déplacement : elle est donc orienté dans le sens opposé à la vitesse.
Son intensité \(R_t = \Vert \vec{R}_t \Vert\) est déterminée par la
loi de Coulomb dynamique :
où \(\mu\) est le coefficient de frottement dynamique. Il s’agit
d’un coefficient phénoménologique sans dimension, dont la valeur est
généralement comprise entre 0 (absence de frottement) et quelques unités
(surface très rugueuse).
En fait, l’égalité () est valable uniquement
lorsque le corps est en mouvement. Si le corps est au repos, la loi de
Coulomb s’exprime sous la forme d’une inégalité :
où \(\mu_s\geq \mu\) est le coefficient de frottement statique.
Pour comprendre cette relation, partons d’une situation initiale où la
surface est horizontale. Si on augmente doucement l’angle d’inclinaison,
le corps reste immobile tant que l’angle est inférieur à une valeur
critique notée \(\alpha_c\). La
relation () devient une égalité au
moment précis où le corps se met en mouvement, c’est-à-dire lorsque
\(\alpha = \alpha_c\). À partir de ce moment, la force de friction
est à nouveau donnée par l’égalité (). Le
coefficient \(\mu_s\) est généralement supérieur à \(\mu\) car
la force requise pour vaincre l’état de repos est plus grande que celle
qui agit sur le solide en mouvement.
Application 4.3: En appliquant le principe fondamental de la dynamique, déterminer la relation entre le coefficient de frottement statique \(\mu_s\) et l’angle critique \(\alpha_c\).
À l’équilibre statique, l’accélération est nulle et donc: \(\sum{\vec{F}}= m \vec{a} = \vec{0}\), et donc:
\[\begin{split}\begin{pmatrix}
m g \sin{\alpha} - R_{t} = 0 \\
-m g \cos{\alpha} + R_{n} = 0
\end{pmatrix}
\Leftrightarrow
\begin{pmatrix}
R_t = m g \sin{\alpha} \\
R_{n}=m g \cos{\alpha}
\end{pmatrix}\end{split}\]
Or, tant que le corps est au repose, on a: \(R_{t} \le \mu_{s} R_{n}\), et donc:
\(\Rightarrow m g \sin{\alpha} \le \mu_{s} m g \cos{\alpha}\)
d’où: \(\boxed{\tan{\alpha}\le \mu_{s}}\)
L’angle critique \(\alpha_{c}\) correspond au moment où le corps se met en mouvement. On a alors l’égalité: \(\boxed{\tan{\alpha_{c}=\mu_{s}}}\)
Nous avons étudié au Chapitre 3 la chute libre d’un point matériel
soumis uniquement à son poids. Lorsque le corps se déplace non pas dans
le vide mais dans un fluide, l’eau ou l’air par exemple, le milieu
exerce une force supplémentaire \(\vec{f}\) qui s’oppose au
mouvement. Cette force de frottement peut s’écrire :
\[\vec{f} = -k \vec{v} \ ,\]
où \(k\) est le coefficient de friction. Celui-ci dépend de la
forme de l’objet, de sa vitesse, ainsi que des propriétés du fluide :
masse volumique \(\rho\) et viscosité \(\eta\).
La viscosité est le paramètre physique qui caractérise la
dissipation d’énergie dans un fluide. Sa dimension est :
\([ \eta ] = M\cdot L^{-1} \cdot T^{-1}\). Elle s’exprime dans le
système international en \(\text{Pa} \cdot \text{s}\). Les valeurs
de \(\rho\) et \(\eta\) à température ambiante
(\(20^{\circ}\text{C}\)) sont données dans la tableau ci-dessous
pour quelques fluides usuels.
L’expression mathématique du coefficient de friction s’obtient en
résolvant les équations de la mécanique des fluides. Sans entrer
dans les détails, on retiendra que l’expression de la force dépend d’un
nombre sans dimension, le nombre de Reynolds :
où \(V\) est la vitesse de l’écoulement et \(L\) la taille de
l’objet.
Application 4.4: Calculer le nombre de Reynolds associé à la nage d’un bactérie dans l’eau (\(L=1~\mu\text{m}\), \(V=1~\mu\text{m}\cdot\text{s}^{-1}\)), et à un parachutiste dans l’air (\(L=2~m\), \(V=200~\text{km}/\text{h}\)).
Nage d’une bactérie dans l’eau: \(\text{Re}=\frac{10^{3}\times 10^{-6} \times 10^{-6}}{10^{-3}}=10^{-6} << 1\) : c’est donc le régime visqueux.
Parachutiste: \(\text{Re}=\frac{1.2 \times 55.5 \times 2}{18 \times 10^{-6}}=7.4\times 10^{6} >> 1\): cést donc le régime inertiel.
On montre alors que :
à faible vitesse (\(\text{Re} \ll 1\)), le coefficient de friction est constant. Pour un objet sphérique de rayon \(a\), il est donné par la formule de Stokes :
où \(S\) est la section transverse de l’objet (\(S=\pi a^2\) pour une sphère de rayon \(a\)), et \(C\) le coefficient de traînée qui dépend de la forme de l’objet.
Application 4.5: Montrer que le coefficient de traînée \(C\) est sans dimension.
Exprimons \(C\): d’après l’équation () on a \(C=\frac{2k}{\rho s v}\).
On connait les dimensions de:
\([rho]=M\cdot L^{-3}\)
\([s]=L^2\)
\([v]=L \cdot T^{-1}\)
Il nous manque seulement les dimensions de \(k\).
On sait que \(\vec{f}=-k \vec{v}\). Écrivons l’équation aux dimensions:
\([k]=\frac{[force]}{[vitesse]} = \frac{M\cdot L \cdot T^{-2}}{L \cdot T^{-1}} = M \cdot T^{-1}\)
On vérifie bien que le coéfficient de trainée est sans dimension.
Formation de parachutistes pratiquant le Free Fly.
Nous pouvons maintenant caractériser le mouvement d’un corps lâché sans
vitesse initiale dans un fluide. Le corps est assimilée à un point
matériel de masse \(m\). Il est soumis aux forces suivantes :
la force de pesanteur \(\vec{P}=m\vec{g}\), qui est verticale et dirigée vers le bas.
la force de frottement \(\vec{f}=-k\vec{v}\), qui est colinéaire au vecteur vitesse mais de sens opposé.
on néglige la poussée d’Archimède, qui sera discutée au Chapitre 8.
En appliquant le principe fondamental de la dynamique au point matériel,
on peut écrire :
Afin de simplifier la discussion, l’axe\((Oz)\)est orienté vers le bas. On projette alors
l’équation () sur cet axe et on divise par \(m\) pour obtenir :
()\[\frac{\text{d}v_z}{\text{d}t} = g - \frac{k}{m}v_z \ .\]
Physiquement, le mouvement de la bille est d’abord accéléré lors du
régime transitoire avant d’atteindre une vitesse constante en
régime stationnaire. Si on s’intéresse uniquement à cette vitesse
limite, il n’est pas nécessaire de résoudre
l’équation (). En effet, le
régime stationnaire correspond à la limite :
Autrement dit, la vitesse limite est atteinte lorsque le poids et la
force de frottement se compensent.
En notant \(v_z(t\to \infty)=v_{\infty}\), on obtient alors les comportements asymptotiques suivants :
dans le régime de Stokes (\(\text{Re} \ll 1\)), la vitesse limite est donnée par : \(v_{\infty} =\displaystyle{\frac{mg}{6\pi \eta a}}\).
dans le régimes \(\text{Re} \gg 1\), on trouve : \(v_{\infty} =\displaystyle{\sqrt{\frac{2mg}{\rho C S}}}\)
Application 4.6: Déterminer la vitesse limite d’un parachutiste en chute libre dans l’air, selon qu’il soit entièrement à l’horizontal où bien à la verticale (voir la fig-ch4_parachute). Dans les deux cas, on proposera une estimation de la section \(S\) du parachutiste et on prendra \(C\approx 0.5\).
Nous avons vu dans l’application 4.4 que le parachutiste est dans le régime où le nombre de Reynolds est \(\text{Re}>>1\), et donc:
\(v_{\infty}=\sqrt{\frac{2m g}{\rho C s}}\)
Pour l’application numérique, on considère une personne de masse 75kg, qui mesure 1.8m. On assimile la section de cette personne à l’horizontal à un rectangle de 0.5m de largeur, et à la verticale à un rectangle de \(0.5m\times0.2m\)
\[\begin{split}C &= 0.5 \\
m &= 75kg \\
\rho&=1.2 kg \cdot m^{-3}\\
g&=9.81 m\cdot s^{-2}\end{split}\]
À l’horizontale, on a \(S=1.8\times 0.5=0.9 m^{2}\) et donc \(v_{\infty}=52.2 m\cdot s^{-1}=187.9 km/h\)
La tête la première: \(S=0.2\times 0.5=0.1 m^{2}\) et donc \(v_{\infty}=156.6 m\cdot s^{-1}=563.7 km/h\)
Note
Considérer que \(C\) est identique dans les deux cas est une appromation discutable, puisqu’il dépend de la forme de l’objet.
Record de vitesse en chute libre
Le record de vitesse en chute libre est détenu par Felix Baumgartner qui a sauté depuis l’altitude de 39km depuis un ballon stratisphérique.
Il a atteint la vitesse de 1342.8 km/h.
