6. Travail, puissance et énergie

6.1) Mouvement d’une bille dans une gouttière \((\ast)\)

Une bille, que l’on assimile à un point matériel de masse \(m=100\) g, se déplace sans frottement le long d’une gouttière cylindrique de rayon \(R=20\) cm — voir la ch6_schemas_a. La bille est lâchée sans vitesse initiale du point \(A\). On souhaite déterminer sa vitesse lorsqu’elle passe au point \(B\).

1. Faire le bilan des forces qui s’appliquent sur la bille.

2. Calculer les travaux des forces entre les points \(A\) et \(B\). Commenter leurs signes.

3. Déduire du théorème de l’énergie cinétique la vitesse \(v\) de la bille au point \(B\). Le résultat dépend-il de la masse \(m\) ? Faire l’application numérique.

4. Expérimentalement, on mesure une vitesse inférieure à la prédiction : \(v_{\textrm{exp}} = 1~\text{m}\cdot \text{s}^{-1}\). La différence étant due aux forces de frottement, calculer le travail de ces dernières entre \(A\) et \(B\).

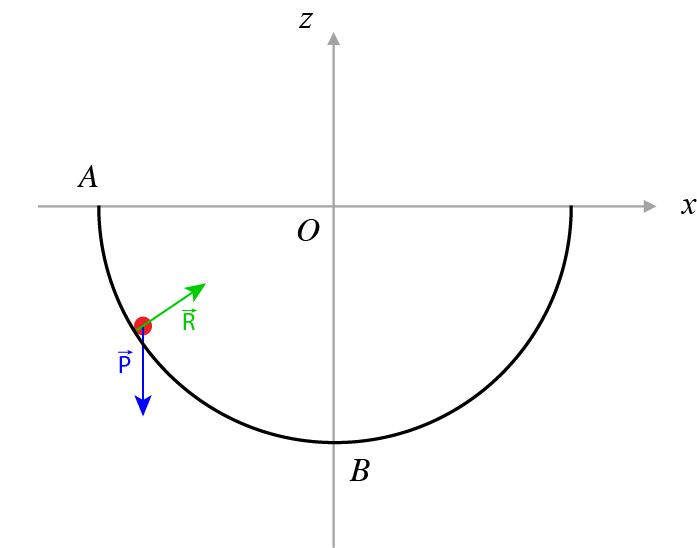
Mouvement d’une bille dans une gouttière

Solution

1. Faire le bilan des forces qui s’appliquent sur la bille.

On néglige les frottements, donc seules s’exercent le poids \(\vec{P}=m\vec{g}\) et la force de réaction de la goutière \(\vec{R}\).

2. Calculer les travaux des forces entre les points \(A\) et \(B\). Commenter leurs signes.

Le travail du poids est donné par:

\[\begin{split}W_{\vec{P}} &= -m g (\underbrace{z_B}_{=-R}-\underbrace{z_A}_{=0}) \\ &= m g R\end{split}\]

Le travail du poids est donc positif et le poids est moteur.

Nous avons vu au Chapitre 4 que par définition la force de réaction est perpendiculaire au support. Donc dans le cas de la bille de notre problème, la force de réaction est à tout instant perpendiculaire au mouvement, et son travail sera donc nul.

\[W_{\vec{R}} = 0\]

3. Déduire du théorème de l’énergie cinétique la vitesse \(v\) de la bille au point \(B`**. Le résultat dépend-il de la masse** :math:`m\) ? Faire l’application numérique.

Dans un référentiel galiléen, la variation de l’énergie cinétique d’un point matériel entre deux points est égale au travail des forces extérieures:

\[\begin{split}\Delta E_c &= \underbrace{E_c^{B}}_{=\frac{1}{2} mv_B^2} - \underbrace{E_c^{A}}_{=0} = \underbrace{W_{\vec{P}}}_{=m g R} + \underbrace{W_{\vec{R}}}_{=0} \\ \Leftrightarrow \frac{1}{2} m v_B^2 &= m g R \\ v_B &= \sqrt{2 g R}\end{split}\]

Donc la vitesse au point B ne dépend pas de la masse de la bille.

Application numérique: \(v_B=\sqrt{2\times9.81\times0.2}=1.98\text{m.s}^{-1}\)

4. Expérimentalement, on mesure une vitesse inférieure à la prédiction : \(v_{\textrm{exp}} = 1~\text{m}\cdot \text{s}^{-1}\) . La différence étant due aux forces de frottement, calculer le travail de ces dernières entre \(A\) et \(B\).

On a:

\[\begin{split}\Delta E_c &= \frac{1}{2} m v_B^2 = \underbrace{W_{\vec{P}}}_{=m g R} + \underbrace{W_{\vec{R}}}_{?} \\ \Rightarrow W_{\vec{R}} &=\frac{1}{2} m v_B^2 - m g R = m \cdot (\frac{1}{2} v_B^2 - g R) \\ W_{\vec{R}} &= 0.1 \times (\frac{1}{2} \times 1^2 - 9.81 \times 0.2) = -0.15 \text{ J}\end{split}\]

On note que le travail de la force de frottement est négatif, ce qui est logique puisque cette force est une force résistive.

6.2) Ski de vitesse \((\ast \ast)\)

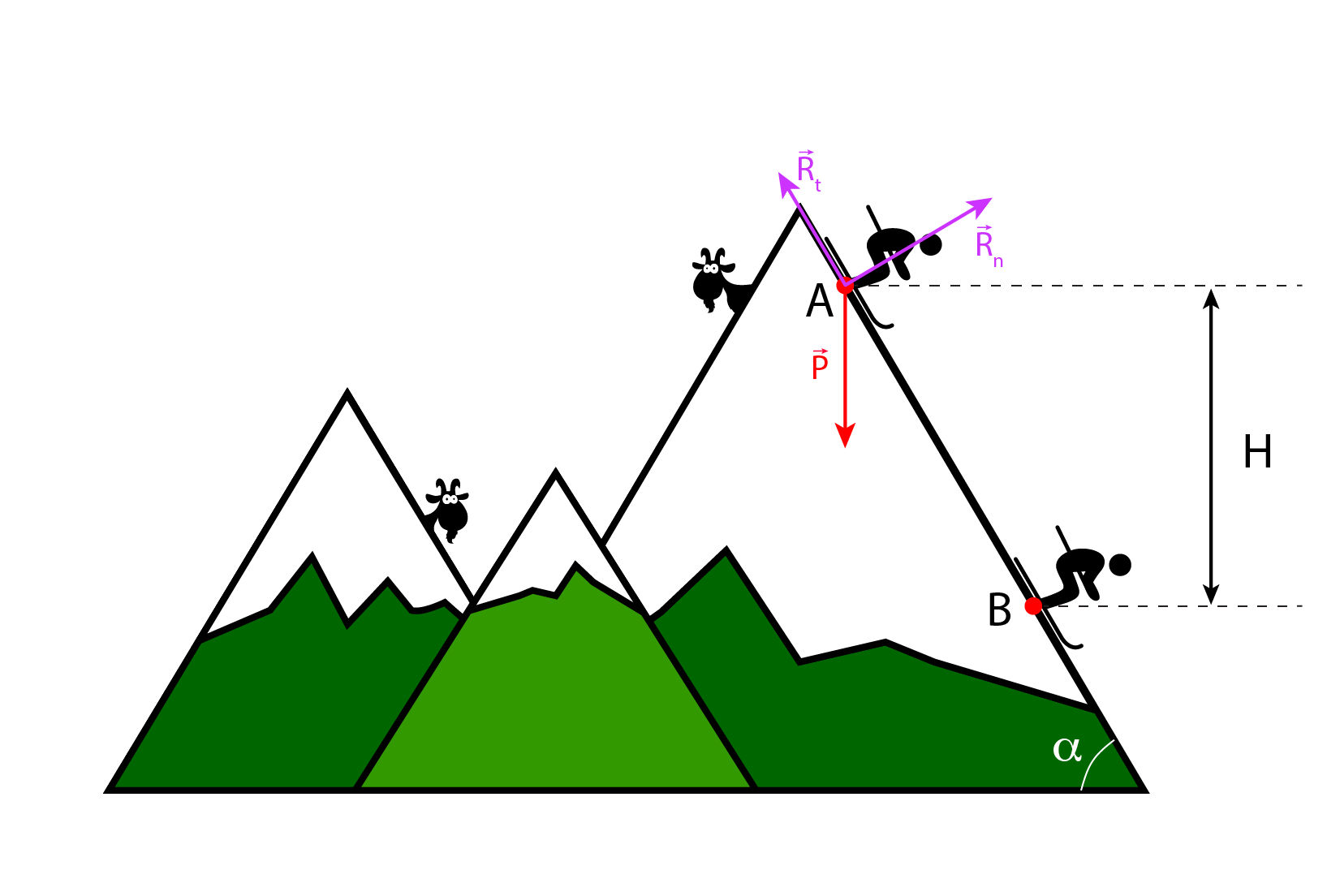
Un skieur s’élance d’un point \(A\) avec une vitesse initiale nulle, sur une piste faisant un angle constant \(\alpha=45^{\circ}\) avec l’horizontale. On souhaite calculer la vitesse \(v\) du skieur au point \(B\). La dénivellation entre \(A\) et \(B\) est \(H=200\) m. Le système {skieur + matériel} est assimilé à un point matériel de masse \(m\). On modélise la friction des skis sur la neige par une force de frottement solide d’intensité \(R_t=\mu R_n\), avec \(\mu = 0,1\).

1. Faire un schéma du problème. Déterminer les forces qui s’exercent sur le skieur.

2. À partir du principe fondamental de la dynamique, établir la relation : \(R_t = \mu mg \cos \alpha\).

3. En déduire le travail de chacune des forces.

4. Finalement, déterminer la vitesse du skieur à l’arrivée en appliquant le théorème de l’énergie cinétique. Faire l’application numérique.

Solution

1. Faire un schéma du problème. Déterminer les forces qui s’exercent sur le skieur.

Le skieur

Le bilan des forces s’écrit:

\[\begin{split}\vec{P}=m \vec{g} \\ \vec{R}_{n} \\ \vec{R_{t}}=\mu R_{n} \vec{e}_x \\\end{split}\]

2. À partir du principe fondamental de la dynamique, établir la relation: \(R_t = \mu mg \cos \alpha\).

Le PDF s’écrit:

\[\begin{split}\vec{P} + \vec{R}_{t} + \vec{R}_{n} = m \vec{a} \\\end{split}\]

avec dans le référential défini dans la ch6-skieur:

\[\begin{split}\vec{P} &= \begin{pmatrix} m g \cos{\big(\frac{\pi}{2}-\alpha\big)} \\ 0 \\ - m g \sin{\big(\frac{\pi}{2}-\alpha\big)} \end{pmatrix} = \begin{pmatrix} m g \sin{\alpha} \\ 0 \\ - m g \cos{\alpha} \end{pmatrix} \\ \vec{R}_{n} &= \begin{pmatrix}0 \\ 0 \\ R_{n} \end{pmatrix} \\ \vec{R}_{t} &= \begin{pmatrix}-R_{t} \\ 0 \\ 0 \end{pmatrix}\end{split}\]

Zoom sur le skieur. On définit le référentiel galiléen (Oxz).

En projetant sur l’axe \((Oz)\) on obtient:

\[-m g \cos{\alpha} + R_{n} = m a_z\]

Or le skieur ne se déplace pas selon l’axe \((Oz)\) de notre repère et donc on a \(a_z=0\) et:

\[\begin{split}-m g \cos{\alpha} + R_{n} = 0 \Leftrightarrow R_{n} = m g \cos{\alpha} \\\end{split}\]

Comme \(R_{t} = \mu R_{n}\) il vient que:

\[\boxed{R_{t} = \mu m g \cos{\alpha}}\]

3. En déduire le travail de chacune des forces.

Le travail de la force de réaction sera nul, puisque celle-ci est toujours perpendiculaire au mouvement:

\[\boxed{W_{\vec{R}_{n}}=0}\]

Seule la composante du poids tangentielle au mouvement va « travailler ». Celle-ci vaut \(m g \sin{\alpha}\) (voir ci-dessus). On aura donc, par définition du travail d’une force constante:

\[W_{\vec{P}}= m g \sin{\alpha} (x_B - x_A)\]

Or \(x_B-x_A = \frac{H}{\cos{\frac{\pi}{2}-\alpha}}=\frac{H}{\sin{\alpha}}\)

Donc:

\[\begin{split}W_{\vec{P}}= m g \sin{\alpha} \frac{H}{\sin{\alpha}} \\ \boxed{W_{\vec{P}}= m g H}\end{split}\]

La force de frottement est purement tangentielle (pas de composante normale). Son travail sera égal à:

\[\begin{split}W_{\vec{R}_t}= -R_t (x_B - x_A) = -\mu m g \cos{\alpha} \frac{H}{\sin{\alpha}} \\ \boxed{W_{\vec{R}_t}=-\frac{\mu mgH}{\tan{\alpha}}}\end{split}\]

Note: attention au signe « - » dans l’expression de \(W_{\vec{R}_t}\) !

4. Finalement, déterminer la vitesse du skieur à l’arrivée en appliquant le théorème de l’énergie cinétique. Faire l’application numérique.

Le théorème de l’énergie cinétique permet d’écrire:

\[\begin{split}\Delta E_c &=\frac{1}{2}m ( v_B^2 - \underbrace{v_A^2}_{=0}) = W_{\vec{P}} + W_{\vec{R}_t} + W_{\vec{R}_n} \\ \frac{1}{2} m v_B^2 &= m g H - \frac{\mu mgH}{\tan{\alpha}} = mgH \cdot \Big( 1-\frac{\mu}{\tan{\alpha}}\Big)\\ v_B &= \sqrt{2gH \Big( 1-\frac{\mu}{\tan{\alpha}}\Big)}\end{split}\]

Application numérique:

\[v_B = \sqrt{2\times 9.81 \times 200 \Big(1-\frac{1}{\tan{\frac{\pi}{4}}}\Big)} = 59.5 \text{ m.s}^{-1} = 214.2 \text{ km.h}^{-1}\]

6.3) Propulsion par un ressort \((\ast \ast )\)

On souhaite utiliser l’énergie emmagasinée par un ressort pour catapulter une bille à la verticale. Le dispositif est représenté sur la ch6_schemas_b: il se compose d’un ressort, de constante de raideur \(k\), qui est comprimé à la moitié de sa longueur à vide \(l_0\). La bille de masse \(m\) est posée à l’extrémité du ressort. L’ensemble est contenu dans un tube afin d’astreindre le mouvement selon \((Oz)\). On relâche alors la contrainte sur le ressort à l’instant initial \(t_i\). On souhaite déterminer la hauteur maximale \(h\) atteinte par la bille à l’instant \(t_f\). Le système étudié est l’ensemble {ressort + bille}. On suppose que les frottements sont négligeables.

Propulsion par un ressort.

1. Donner les expressions des énergies cinétiques et potentielles à l’instant \(t_i\).

2. Procéder de même à l’instant \(t_f\).

3. En appliquant le théorème de l’énergie mécanique, déterminer \(h\).

Solution

1. Donner les expressions des énergies cinétiques et potentielles à l’instant \(t_i\).

• Énergie cinétique:

\[\boxed{E_c=\frac{1}{2} m v_i^2 = 0 \text{ car }v_i=0}\]

• Énergie potentielle du poids:

  Exprimons le travail élémentaire du poids \(\delta W_{\vec{P}} = \vec{P}\cdot\vec{d\ell} = -m g \vec{e}_{z} \cdot dz \vec{e}_{z} = -mg dz\).

  Or par définition de l’énergie potentielle: \(\delta W_{\vec{P}}=-dE_p(\vec{P}) \Leftrightarrow \parder{E_p(\vec{P})}{z}=mg\).

  En intégrant, on obtient: \(E_p(\vec{P})=mgz + C_1\) où \(C_1\) est une constante.

  À l’instant initial \(t_i\) on a \(z=\frac{l_0}{2}\) et cette expression devient: \(\boxed{E_p^i(\vec{P})=mg\frac{l_0}{2} + C_1}\).

• Énergie potentielle du ressort:

  Exprimons le travail élementaire de la force élastique: \(\delta W_{\vec{F}}=\vec{F}\cdot \vec{d\ell} = -k (z-l_0) \vec{e}_{z} \cdot dz \vec{e}_z =-k (z-l_0) dz\)

  Or par définition de l’énergie potentielle: \(\delta W_{\vec{F}}=-dE_p(\vec{F}) \Leftrightarrow \parder{E_p(\vec{F})}{z}= k (z-l_0)\).

  En intégrant, on obtient: \(E_p(\vec{P})=\frac{1}{2} k (z-l_0)^2 + C_2\) où \(C_2\) est une constante.

  À l’instant initial \(t_i\) on a \(z=\frac{l_0}{2}\) et cette expression devient: \(\boxed{E_p^i(\vec{F})=\frac{k l_0^2}{8} + C_2}\).

2. Procéder de même à l’instant \(t_f\).

• Énergie cinétique:

\[\boxed{E_c=\frac{1}{2} m v_f^2 = 0 \text{ car }v_f=0}\]

• Énergie potentielle du poids: la balle est alors à la hauteur \(h\) et donc: \(\boxed{E_p^f(\vec{P})=mgh + C_1}\)

• Énergie potentielle du ressort: une fois la balle éjectée, le ressort est à sa position de repos et \(z=l_0\), et donc \(\boxed{E_p^f(\vec{F})= \frac{1}{2} k (l_0-l_0)^2 + C_2 = C_2}\).

3. En appliquant le théorème de l’énergie mécanique, déterminer \(h\).

Exprimons l’énergie mécanique dans l’état initial et dans l’état final:

\[\begin{split}E_m^i &= E_c^i + E_p^i(\vec{P}) + E_p^i(\vec{F}) = mg\frac{l_0}{2} + C_1 + \frac{k l_0^2}{8} + C_2 \\ E_m^f &= E_c^f + E_p^f(\vec{P}) + E_p^f(\vec{F}) = mgh + C_1 + C_2\end{split}\]

Puisque les forces qui s’appliquent (le poids et la force élastique) sont toutes les deux conservatives, l’énergie mécanique du système doit être constante et \(E_m^i=E_m^f\), ce qui s’écrit:

\[\begin{split}\Delta E_m &=E_m^f - E_m^i = 0 = (mgh + C_1 + C_2) - (mg\frac{l_0}{2} + C_1 + \frac{k l_0^2}{8} + C_2) \\ \Rightarrow mgh &= mg\frac{l_0}{2} +\frac{k l_0^2}{8}\end{split}\]

\[\boxed{h = \frac{l_0}{2} + \frac{k l_0^2}{8gm}}\]

6.4) Vitesse de libération \((\ast \ast)\)

Pour qu’une sonde spatiale échappe à l’attraction gravitationnelle d’une planète, il faut que sa vitesse soit supérieure à une valeur seuil : la vitesse de libération \(v_l\). Nous allons appliquer le théorème de l’énergie mécanique afin de déterminer cette vitesse en fonction du rayon \(R\) et de la masse \(M\) de la planète. On note \(\mathcal{G}=6,7 \times 10^{-11}\) SI la constante universelle de gravitation.

1. Rappeler l’expression de la force d’attraction \(\vec{F}\) qui s’exerce sur la sonde de masse \(m\).

2. Établir l’expression de l’énergie potentiel de gravitation \(E_p(r)\). Pour fixer la constante, on prendra : \(E_p(r\to \infty)=0\).

3. On suppose que la sonde est soumise uniquement à l’attraction gravitationnelle. Donner l’expression générale de son énergie mécanique \(E_m\). Que vaut cette énergie lorsque \(r \to \infty\)?

4. En déduire la vitesse minimale \(v_l\) que doit atteindre la sonde pour échapper à l’attraction de la planète.

5. Calculer la valeur numérique de \(v_l\) pour les planètes suivantes :

   • Terre : \(R=6,4 \times 10^6\) m et \(M=6,0\times 10^{24}\) kg

   • Pluton : \(R=1,2 \times 10^6\) m et \(M=1,3\times 10^{22}\) kg

   • Jupiter : \(R=7,0 \times 10^7\) m et \(M=1,9\times 10^{27}\) kg

Solution

1. Rappeler l’expression de la force d’attraction \(\vec{F}\) qui s’exerce sur la sonde de masse \(m\).

Nous avons vu au chapitre 5 que:

\[\vec{F} = - \mathcal{G} \frac{m_P m}{r^2}\vec{e}_r\]

où \(m_P\) est la masse de la planète et \(r\) la distance entre le satellite et le centre de masse de la planète

2. Établir l’expression de l’énergie potentiel de gravitation \(E_p(r)\). Pour fixer la constante, on prendra: \(E_p(r\to \infty)=0\).

Exprimons le travail élémentaire de la force de gravitation sur un déplacement élémentaire \(d\vec{\ell}=dr \vec{e}_{r}\):

\[\begin{split}\delta W &= \vec{F} \cdot d \vec{\ell} \\ &= - \mathcal{G} \frac{m_P m}{r^2} \vec{e}_r \cdot dr \vec{e}_r \\ &= -\mathcal{G} \frac{m_P m}{r^2} dr\end{split}\]

La force gravitationnelle étant conservative, il existe une énergie potentielle associée à la force gravitationnelle telle que:

\[dE_p = - \delta W = \mathcal{G} \frac{m_P m}{r^2} dr\]

On déduit en prenant la primitive que:

\[E_p = -\mathcal{G} \frac{m_P m}{r} + C\]

où \(C\) est une constante. On trouve immédiatement que celle-ci vaut 0 puisque puisque \(E_p(r\to \infty)= C = 0\).

3. On suppose que la sonde est soumise uniquement à l’attraction gravitationnelle. Donner l’expression générale de son énergie mécanique \(E_m\). Que vaut cette énergie lorsque \(r \to \infty\)?

On appelle énergie mécanique \(E_m\) d’un point matériel la somme de son énergie cinétique et son énergie potentielle : \(E_m = E_c +E_p\).

Donc ici:

\[E_m = \frac{1}{2}m v^2 -\mathcal{G} \frac{m_P m}{r}\]

Lorsque \(r \to infty\), on voit que l’énergie potentielle tend vers 0 et l’énergie mécanique est égale à l’énergie cinétique: \(E_m = \frac{1}{2} m v^2\)

4. En déduire la vitesse minimale \(v_l\) que doit atteindre la sonde pour échapper à l’attraction de la planète.

On veut que la sonde s’échappe de l’attraction gravitationnelle, c’est à dire qu’elle puisse s’éloigner indéfiniment de la planète. Considérons donc le trajet de la sonde depuis une distance \(r\) (position initiale) jusqu’à l’infini (position finale). La vitesse initiale minimale pour échapper à l’attraction gravitionnelle correspond à la vitesse initiale qui donnera une vitesse finale nulle à l’infini. Si la vitesse à l’infini est nulle, alors l’énergie mécanique de l’objet à l’infini est nulle également, puisque \(E_m(\infty) = E_c = \frac{1}{2} m \underbrace{v_{\infty}^2}_{=0} = 0\). Or comme l’énergie mécanique se conserve (car la force gravitationnelle est conservative), on doit avoir à l’instant initial:

\[E_m^{ini}=E_m^{fin} = 0\]

Or, à l’instant initial l’énergie mécanique vaut: \(E_m = \frac{1}{2} m v_{l}^2 -\mathcal{G} \frac{m_P m}{r}\).

On déduit que:

\[\begin{split}\frac{1}{2} m v_{l}^2 -\mathcal{G} \frac{m_P m}{r} &= 0 \\ \Leftrightarrow v_l = \sqrt{\frac{2 \mathcal{G} m_P}{r}}\end{split}\]

5. Calculer la valeur numérique de \(v_l\) pour les planètes suivantes […]

• Terre: 11.2 km/s

• Pluton: 1.2 km/s

• Jupiter: 60.2 km/s

6.5) Résistance de l’air \((\ast \ast \ast)\)

Un point matériel \(M\) de masse \(m\) a un mouvement rectiligne suivant l’axe horizontal \((Ox)\). Il est soumis uniquement à la résistance de l’air, que l’on modélise par une force d’intensité \(f=\beta v^2\). À l’instant initial \(t=0\), le point matériel se trouve en \(x=0\) et sa vitesse est \(v_0\).

1. En appliquant le principe fondamental de la dynamique, montrer que la vitesse est donnée par :

   \[v(t) = \frac{v_0}{1+t/\tau} \ ,\]

   où \(\tau\) et une constante que l’on exprimera en fonction de \(m\) et \(\beta\). Tracer \(v(t)\).

2. Calculer le travail de la force de friction entre les instants \(t=0\) et \(t=\tau\). Pour cela, on procédera de deux façons :

   • en évaluant directement l’intégrale définissant le travail.

   • en appliquant le théorème de l’énergie cinétique.

Solution

1. En appliquant le principe fondamental de la dynamique, montrer que la vitesse est donnée par […]

• Système: le mobile

• Référentiel: \((Oxz)\) (voir td6_ex5)

• Bilan des forces:

  \[\begin{split}\vec{P}&=\begin{pmatrix}0 \\ -mg\end{pmatrix}\\ \vec{R}&=\begin{pmatrix}0 \\ R \end{pmatrix} \\ \vec{f} &= \begin{pmatrix}-\beta v_x^2 \\ 0 \end{pmatrix}\end{split}\]

Schéma du problème.

Le principe fondamental de la dynamique s’écrit:

\[m\vec{a} = \vec{P} + \vec{R} + \vec{f}\]

Soit en projetant sur les axes:

\[\begin{split}(Ox) &: m a_x = m \parder{v_x}{t} = 0 + 0 - \beta v_x^2 \\ (Oz) &: m a_z = 0 = -mg + R +0 \text{ (car mouvement horizontal exclusivement)}\\\end{split}\]

On déduit immédiatement de la projection suivant \((Oz)\) que \(R=mg\), mais ce n’est pas vraiment ce qui nous intéresse. On va donc étudier la projection suivant \((Ox)\):

\[m\parder{v_x}{t} = -\beta v^2 \Leftrightarrow \parder{v_x}{t} +\frac{\beta}{m} v_x^2\]

D’après l’énoncé on cherche une solution de la forme: \(v_x(t)=\frac{v_0}{1+\frac{t}{\tau}}=\frac{v_0 \tau}{t+\tau}\). On a alors:

\[\begin{split}v_x^2(t) &=\frac{v_0^2 \tau^2}{(t+\tau)^2}\\ \parder{v_x(t)}{t} &= -\frac{v_0 \tau}{(t+\tau)^2}\end{split}\]

ce qui nous donne:

\[\parder{v_x}{t} +\frac{\beta}{m} v_x^2 = -\frac{v_0 \tau}{(t+\tau)^2} + \frac{\beta}{m} \frac{v_0^2 \tau^2}{(t+\tau)^2} = 0\]

ce qui ne peut être vérifié quelque soit \(t\) que si \(\boxed{\tau=\frac{m}{v_0 \beta}}\), et alors:

\[v(t)=\frac{v_0}{1+\frac{t}{\tau}}=\frac{v_0}{1+\frac{\beta v_0 t}{m}}\]

2. Calculer le travail de la force de friction entre les instants […]

- en évaluant directement l’intégrale définissant le travail

Par définition:

\[\begin{split}\delta W(\vec{f}) &=\vec{f} \cdot \vec{d\ell} \\ &= -\beta\ v_x^2(t)\ \vec{e}_{x}\ v(t)\ dt\ \vec{e}_x &= \beta v_x^3(t) dt\end{split}\]

car \(\vec{d \ell}=\vec{v}\ dt =\vec{v}_x\ dt\ \vec{e}_x\)

Donc:

\[\begin{split}W(\vec{f})_{0\to \tau} &= \int_{0}^{\tau} -\beta v_x^3(t) dt \\ &= \int_{0}^{\tau} -\beta \frac{v_0^3}{(1+\frac{t}{\tau})^3} dt \\ &= -\beta v_0^3 \int_{0}^{\tau} \frac{1}{(1+\frac{t}{\tau})^3} dt \\ &= \beta v_0^3 \int_{0}^{\tau} \left(\frac{\tau}{\tau+t}\right)^3 dt \\ &= \beta v_0^3 \tau^3 \int_{0}^{\tau} \frac{1}{(\tau+t)^3} dt\end{split}\]

Faisons un changement de variable: on pose \(f=(\tau+t)\) On a alors

\[\begin{split}f'(t) &=\parder{(\tau+t)}{t} = 1 \\ \text{et} & \\ \frac{1}{(\tau +t)^3} &= \frac{1}{f^3} = f' \cdot f^{-3}\end{split}\]

Rappels

La primitive d’une fonction composée de la forme \(f'\cdot f^n\ \ (n\ne1)\) est égale à:

\[\int (f'\cdot f^n) =\frac{1}{n+1} f^{n+1}\]

Ici on a \(n=-3\) et donc:

\[\int f'\cdot f^{-3} =\frac{1}{-3+1} f^{-3+1}=-\frac{1}{2} f^{-2}=-\frac{1}{2} (\tau+t)^{-2}\]

L’équation précédente entre 0 et \(\tau\) s’écrit donc:

\[\begin{split}W(\vec{f})_{0\to \tau} &= -\beta v_0^3 \tau^3 \left( \underbrace{-\frac{1}{2} (\tau+\tau)^{-2}}_{t=\tau} - \left(\underbrace{-\frac{1}{2} (\tau+0)^{-2}}_{t=0}\right)\right) \\ &= -\beta v_0^3 \tau^3 \left(\frac{1}{2}\frac{1}{(2\tau)^{2}} + \frac{1}{2} \frac{1}{\tau^2} \right)\\ &= -\beta v_0^3 \tau^3 \left(\frac{1}{8\tau^2} - \frac{1}{2\tau^2}\right) \\ &= -\beta v_0^3 \tau^3 \frac{1}{\tau^2} \left(\frac{1}{8}-\frac{1}{2} \right) = -\beta v_0^3 \tau \frac{3}{8}\end{split}\]

en replaçant \(\tau=\frac{m}{v_0 \beta}\) on obtient finalement:

\[\boxed{W(\vec{f})_{0\to \tau} = -\frac{3}{8} m v_0^2}\]

- en appliquant le théorème de l’énergie cinétique

D’après le théorème de l’énergie cinétique, la variation d’énergie cinétique entre deux instants est égale à la somme des travaux de toutes les forces extérieures entre ces deux instants. Donc ici:

\[\Delta E_c^{0\to \tau} = W^{0\to \tau}(\vec{P}) + W^{0\to \tau}(\vec{R}) +W^{0\to \tau}(\vec{f})\]

Les travaux du poids et de la force de réaction du support sont tous les deux nuls car ces deux forces sont perpendiculaires au mouvement. Il reste donc:

\[\begin{split}\Delta E_c^{0\to \tau} &= W_{\vec{f}}^{0\to \tau} =\frac{1}{2} m v^2(\tau)-\frac{1}{2} m v_0^2 \\ &= \frac{1}{2} m \Big(\frac{v_0}{1+\frac{\tau}{\tau}}\Big)^2 - \frac{1}{2} m v_0^2 \\ &= \frac{1}{2} m v_0^2 \Big(\frac{1}{(1+1)^2}-1\Big) \\ &= \frac{1}{2} m v_0^2 \Big(\frac{1}{4} - 1\Big) \\\end{split}\]

\[\boxed{\Delta E_c^{0\to \tau} = W_{\vec{f}}^{0\to \tau} = -\frac{3}{8} m v_0^2}\]

On retrouve bien la même expression.

Note

On note que le travail est négatif, ce qui est logique puisque la force de frottement s’oppose au mouvement et est une force résistive.

6.6) Rebonds d’une balle de tennis \((\ast \ast \ast)\)

On considère une balle de tennis que l’on lâche sans vitesse initiale d’une hauteur \(h_0\). La balle rebondit plusieurs fois au sol. On suppose que lors du choc, une fraction \(\epsilon <1\) de l’énergie mécanique est perdue par la balle. On néglige les frottements avec l’air durant les phases de chute libre. Calculer la hauteur \(h_n\) du \(n\)-ième rebond de la balle, ainsi que le temps total \(T_n\) de l’ensemble des rebonds.

Solution

Exprimons la hauteur atteinte pour les 3 premiers rebonds.

Rebond nº1:

À l’instant \(t=0\), la vitesse est nulle et l’énergie mécanique initiale de la balle de tennis vaut:

\[\begin{split}E_m^0 &= E_c^0 + E_p^0 = \frac{1}{2} m \underbrace{v_0^2}_{=0} + m g h_0\\ \Rightarrow E_m^0 &= m g h_0\end{split}\]

De la même manière, l’énergie mécanique au sommet du premier rebond sera égale à:

\[\begin{split}E_m^1 &= E_c^1 + E_p^1 = \frac{1}{2} m \underbrace{v_1^2}_{=0} + m g h_1\\ \Rightarrow E_m^1 &= m g h_1\end{split}\]

puisque au sommet du rebond la vitesse est toujours nulle.

D’après l’énoncé, la variation de l’énergie mécanique entre deux rebonds successifs est égale à: \(\Delta E_m^{0\to 1}=E_m^1-E_m^0= -\epsilon E_m^0 = -\epsilon m g h_0\).

Avertissement

Attention au signe moins: l’énergie mécanique du premier rebond est inférieure à l’énergie mécanique initiale.

On peut donc écrire:

\[\begin{split}\Delta E_m^{0\to 1} &=E_m^1-E_m^0 = mgh_1 - mgh_0 = -\epsilon m g h_0\\ \Leftrightarrow h_1 &= h_0 - \epsilon h_0 \\\end{split}\]

soit finalement:

\[\boxed{h_1= h_0 \cdot (1-\epsilon)}\]

Rebond nº2:

En raisonnant de la même manière, on peut écrire:

\[\Delta E_m^{1\to2}=E_m^2-E_m^1= -\epsilon E_m^1\]

avec:

• \(E_m^2 = E_c^2 + E_p^2 = \frac{1}{2} m \underbrace{v_2^2}_{=0} + m g h_2\)

• \(E_m^1 = m g h_1 = m g h_0 \cdot (1-\epsilon)\) puisque \(h_1 = h_0 \cdot (1-\epsilon)\)

On obtient donc:

\[\begin{split}E_m^2-E_m^1 &= -\epsilon E_m^1 \\ \Leftrightarrow mgh_2 - mg h_1 &= -\epsilon m g h_1\\ \Leftrightarrow h_2 - h_1 &= -\epsilon h_1 \\ \Leftrightarrow h_2 &= h_1 -\epsilon h_1 = h_1 (1-\epsilon) \\ \Leftrightarrow h_2 &= \underbrace{ h_0 \cdot (1-\epsilon) }_{=h_1} (1-\epsilon)\end{split}\]

soit finalement:

\[\boxed{h_2 = h_0 \cdot (1-\epsilon)^2}\]

Rebond nº3:

Toujour en raisonnant de la même manière, on peut écrire:

\[\Delta E_m^{2\to3}=E_m^3-E_m^2= -\epsilon E_m^2\]

avec:

• \(E_m^3 = E_c^3 + E_p^3 = \frac{1}{2} m \underbrace{v_3^2}_{=0} + m g h_3\)

• \(E_m^2 = m g h_2 = m g h_0 \cdot (1-\epsilon)^2\) puisque \(h_2 = h_0 \cdot (1-\epsilon)^2\)

On obtient donc:

\[\begin{split}E_m^3-E_m^2 &= -\epsilon E_m^2 \\ \Leftrightarrow mgh_3 - mg h_2 &= -\epsilon m g h_2\\ \Leftrightarrow h_3 - h_2 &= -\epsilon h_2 \\ \Leftrightarrow h_3 &= h_2 -\epsilon h_2 = h_2 (1-\epsilon) \\ \Leftrightarrow h_3 &= \underbrace{ h_0 \cdot (1-\epsilon)^2 }_{=h_2} (1-\epsilon)\end{split}\]

soit finalement:

\[\boxed{h_3 = h_0 \cdot (1-\epsilon)^3}\]

On voit apparaître une relation simple entre le rebond numéro \(n\) et sa hauteur:

\[\boxed{h_n = h_0 \cdot (1-\epsilon)^n}\]

Étudions maintenant le temps total des rebonds. Nous avons vu au Chapitre 3 (dans l’exercice 3.3) que le temps de la chute depuis une hauteur \(h_n\) est égale à: \(t_n = \sqrt{\frac{2h_n}{g}}\). En remplaçant \(h_n\) par l’expression déterminée ci-dessus on obtient:

\[t_n = \sqrt{\frac{2 h_0 (1-\epsilon)^n}{g}}\]

Le temps total des rebonds est donné par la somme de tous les temps de chute, plus tous les temps d’ascension. Or les temps d’ascension depuis le sol jusqu’à la hauteur \(h_n\) sont égaux au temps de chute depuis cette même hauteur \(h_n\). Le temps total est donc égal à:

\[\begin{split}T_n &= t_0 + 2t_1 + 2t_2 + 2 t_3 + ... + 2 t_n \\ &= \sqrt{\frac{2h_0}{g}} + 2 \sqrt{\frac{2 h_0 (1-\epsilon)}{g}} + 2 \sqrt{\frac{2 h_0 (1-\epsilon)^2}{g}} + ... + 2 \sqrt{\frac{2 h_0 (1-\epsilon)^n}{g}}\\ &= \sqrt{\frac{2h_0}{g}} \Big(1 + 2\sqrt{(1-\epsilon)} + 2\sqrt{(1-\epsilon)^2} + 2\sqrt{(1-\epsilon)^3} + ... + 2\sqrt{(1-\epsilon)^n} \Big) \\ &= 2 \sqrt{\frac{2h_0}{g}} \Big(\frac{1}{2} + (1-\epsilon)^{1/2} + (1-\epsilon)^{2/2} + (1-\epsilon)^{3/2} + ... + (1-\epsilon)^{n/2}\Big)\end{split}\]

On reconnait (presque) l’expression de la somme des termes d’une suite géométrique de raison \(q=(1-\epsilon)^{1/2}\) et de premier terme \(u_0=1\):

\[\sum_{k=0}^{n} u_k = 1 + (1-\epsilon)^{1/2} + (1-\epsilon)^{2/2} + (1-\epsilon)^{3/2} + ... + (1-\epsilon)^{n/2}\]

Rappels

La somme d’une telle suite géométrique vérifie:

\[\sum_{k = 0}^{n} u_k = u_0 + ⋯ + u_n = u_0 ( 1 + q + ⋯ + q^n ) = u_0 \frac{1 − q^{n + 1}}{1 − q}\]

Avertissement

On voit que le premier terme de cette suite vaut 1 et ne correspond pas exactement au premier terme présent dans l’expression de \(T_n\) qui est \(\frac{1}{2}\)! Il faudra prendre soin de soustraire \(\frac{1}{2}\sqrt{\frac{2h_0}{g}}\) à la somme des termes de cette suite.

Dans notre cas, on obtient donc:

\[\begin{split}T_n &= 2 \sqrt{\frac{2h_0}{g}} \Big(\frac{1- (1-\epsilon)^{(n+1)/2}}{1- (1-\epsilon)^{1/2}}\Big) - \frac{1}{2}\sqrt{\frac{2h_0}{g}} \\ &= 2 \sqrt{\frac{2h_0}{g}} \left(\frac{1- (1-\epsilon)^{(n+1)/2}}{1- (1-\epsilon)^{1/2}} -\frac{1}{4}\right)\end{split}\]