2. Cinématique du point

La cinématique a pour objet l’étude des mouvements, indépendamment des causes qui les produisent. Dans ce chapitre, nous introduisons les notions de vitesse et d’accélération dont nous aurons besoin par la suite afin de caractériser les trajectoires en mécanique du point.

Rappels sur les vecteurs

On peut distinguer deux types de grandeurs physiques : les scalaires, qui sont spécifiés par un nombre et éventuellement une unité, et les vecteurs, caractérisés par une direction, un sens et une norme. La norme étant elle-même un scalaire, elle peut également avoir une dimension. Nous commençons par rappeler quelques propriétés des vecteurs, qui seront utiles par la suite.

Définition

Un vecteur est un segment orienté, ayant pour extrémités un point de départ et un point d’arrivée, que l’on note respectivement \(A\) et \(B\) pour fixer les idées. Le vecteur \(\overrightarrow{AB}\) ainsi formé est défini par :

• sa direction, la droite \((AB)\).

• son sens, du point \(A\) vers le point \(B\).

• sa norme, qui correspond à la longueur du segment \([AB]\).

On note en particulier que les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{BA}\) ont même direction et même norme, mais ils sont de sens opposé : \(\overrightarrow{BA}=-\overrightarrow{AB}\).

Une propriété importante des vecteurs est la relation de Chasles. Pour tous points \(A\), \(B\) et \(C\), on a la relation d’addition suivante :

\[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC} \ .\]

D’un point de vue géométrique, cette relation implique que l’addition de deux vecteurs s’effectue selon la méthode du triangle — voir la fig-ch2-chasles (a) : on fait coïncider l’origine du second vecteur avec l’extrémité du premier. La somme s’obtient alors en joignant l’origine du premier vecteur avec l’extrémité du second.

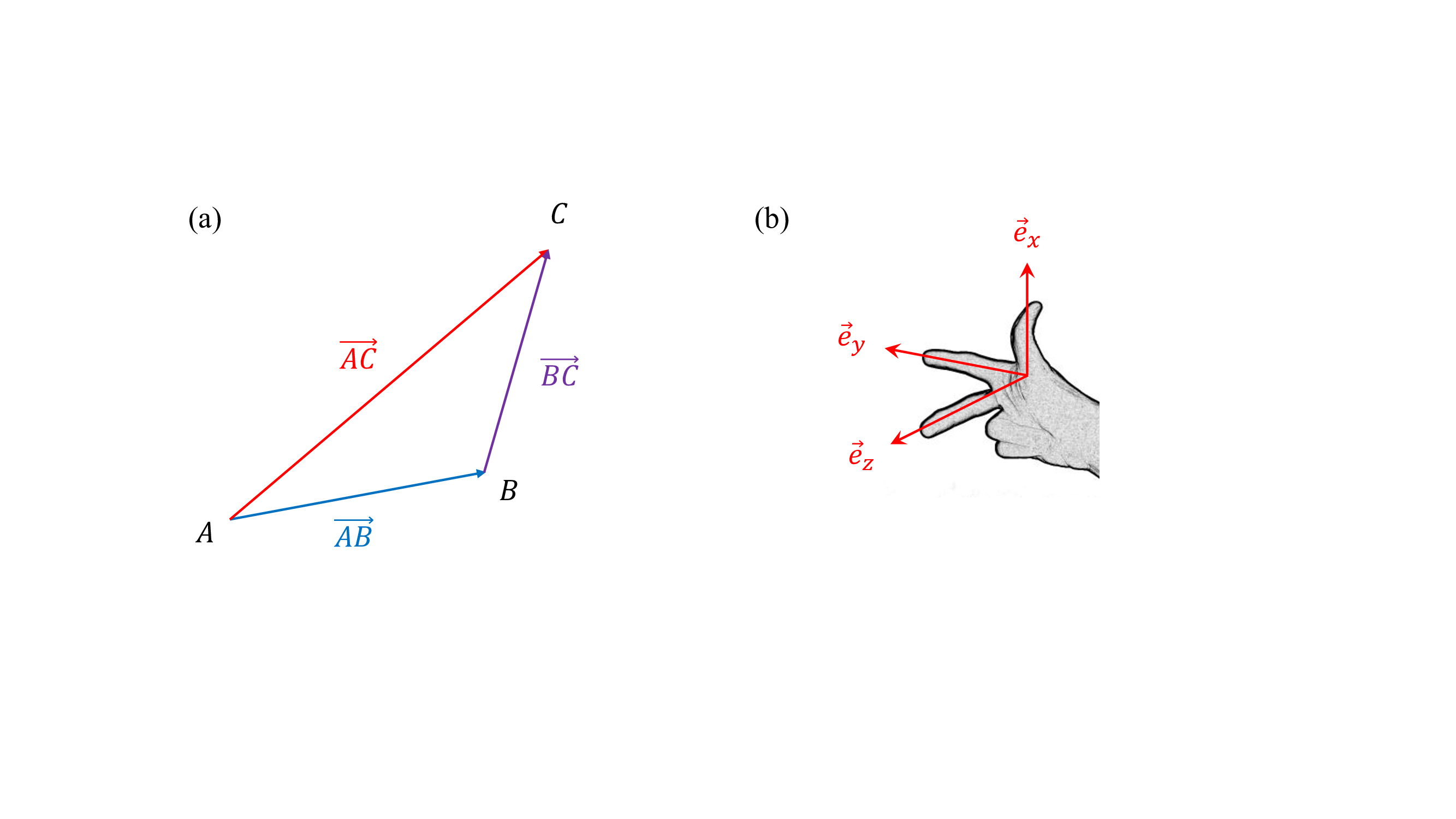
(a) Illustration de la relation de Chasles. (b) Définition d’une base directe à partir de la règle des trois doigts de la main droite : le pouce donne le sens de \(\vec{e}_x\), l’index celui de \(\vec{e}_y\) et le majeur celui de \(\vec{e}_z\).

Coordonnées cartésiennes

Pour repérer la position d’un point dans l’espace, on définit le repère cartésien qui est constitué d’une origine, \(O\), et de trois vecteurs \(\vec{e}_x\), \(\vec{e}_y\) et \(\vec{e}_z\) qui sont tels tels que :

• les vecteurs sont unitaires : \(\Vert \vec{e}_x\Vert =\Vert \vec{e}_y \Vert = \Vert \vec{e}_z \Vert = 1\).

• ils sont orthogonaux deux à deux.

• ils forment un trièdre directe, comme illustré sur la fig-ch2-chasles (b)

Le repère cartésien est un repère orthonormé direct. Dans ce repère, la position d’un point \(M\) est repérée par ses coordonnées \((x,y,z)\), qui correspondent aux projections orthogonales de \(M\) sur les axes \((Ox)\), \((Oy)\) et \((Oz)\) — voir la fig-ch2-coords (a). De façon équivalente, le vecteur \(\overrightarrow{OM}\) peut s’écrire :

\[\begin{split}\overrightarrow{OM}= x \vec{e}_x + y \vec{e_y} + z \vec{e}_z = \begin{pmatrix} x \\ y \\ z \end{pmatrix} \ .\end{split}\]

Plus généralement, si deux points \(A\) et \(B\) ont pour coordonnées \(A(x_A,y_A,z_A)\) et \(B(x_B,y_B,z_B)\), alors le vecteur \(\overrightarrow{AB}\) a pour composantes :

\[\begin{split}\overrightarrow{AB}= \overrightarrow{OB} -\overrightarrow{OA}= \begin{pmatrix} x_B-x_A \\ y_B-y_A \\ z_B-z_A \end{pmatrix} \ .\end{split}\]

(a) Définition des coordonnées d’un point \(M\) dans la base cartésienne. (b) Produit scalaire entre deux vecteurs.

Produit scalaire et norme

Dans un repère cartésien, la norme du vecteur \(\vec{u} = u_x \vec{e}_x + u_y \vec{e_y} + u_z \vec{e}_z\) est donnée par :

\[\Vert \vec{u} \Vert = \sqrt{u_x^2 + u_y^2 + u_z^2} \ .\]

On définit également le produit scalaire entre \(\vec{u}\) et le vecteur \(\vec{v} = v_x \vec{e}_x + v_y \vec{e_y} + v_z \vec{e}_z\) :

\[\vec{u} \cdot \vec{v} = u_xv_x + u_yv_y + u_zv_z \ .\]

Le produit scalaire vérifie les propriétés suivantes :

\[\vec{u}\cdot\vec{v} = \vec{v}\cdot\vec{u} \ , \quad \text{et} \quad \vec{u}\cdot \vec{u} = \Vert \vec{u} \Vert^2 \ .\]

D’un point de vue géométrique, le produit scalaire est relié à l’angle \(\theta\) entre les vecteurs. Supposons en effet que les deux vecteurs \(\vec{u}\) et \(\vec{v}\) sont dans le plan \(Oxy\), comme représenté sur la fig-ch2-coords (b). Pour simplifier, on choisit l’axe \((Ox)\) tel que le vecteur \(\vec{u}\) lui soit colinéaire. Un soupçon de trigonométrie permet alors d’obtenir :

()\[\vec{u}\cdot\vec{v} = \Vert \vec{u} \Vert \times \Vert \vec{v} \Vert \times \cos \theta\]

Application 2.1: Démontrer la relation \(\vec{u}\cdot\vec{v} = \Vert \vec{u} \Vert \times \Vert \vec{v} \Vert \times \cos \theta\)

Pour simplifier les notations, on notera \(u=\Vert \vec{u} \Vert\) et \(v=\Vert \vec{v} \Vert\).

Les coordonnées des deux vecteurs s’écrivent (voir fig-ch2-coords):

\[\begin{split}\vec{u}=\begin{pmatrix} u \\ 0 \end{pmatrix} \, \, ; \, \, \vec{v}=\begin{pmatrix} v \cos{\theta} \\ v \sin{\theta} \end{pmatrix}\end{split}\]

et donc, par définition du produit scalaire:

\[\begin{split}\vec{u}\cdot\vec{v} &= u_x \cdot v_x + u_y \cdot v_y \\ &= u v \cos{\theta} + 0 &= u v \cos{\theta}\end{split}\]

Dans le cas particulier où \(\vec{u}=\vec{e}_x\), on obtient donc : \(\vec{v}\cdot\vec{e_x}=v_x\). Ce résultat peut se généraliser à 3 dimensions. On retiendra que les coordonnées d’un vecteur s’obtiennent par projection sur les vecteurs de base :

\[v_x = \vec{v}\cdot\vec{e_x} \ , \quad v_y = \vec{v}\cdot\vec{e_y} \ , \quad \text{et} \quad v_z = \vec{v}\cdot\vec{e_z} \ .\]

Vitesse et accélération

Appliquons maintenant les propriétés des vecteurs pour décrire les trajectoires. La trajectoire d’un point \(M\) est définie comme l’ensemble des positions occupées par le point \(M\) au cours du temps. Nous discutons d’abord le cas unidimensionnel avant de généraliser les notions de vitesse et d’accélération à un mouvement quelconque.

Mouvement unidimensionnel

Considérons tout d’abord le mouvement d’un point le long d’une droite, l’axe \((Ox)\) pour fixer les idées. La position du point \(M\) à un instant \(t\) est décrite par son abscisse \(x(t)\), qui est donc une fonction de la variable \(t\). On définit alors la vitesse du point \(M\) comme la dérivée de la position :

()\[\boxed{v_x(t) = \frac{d x}{d t} \ .}\]

En terme de dimension, on a : \([v_x] = \frac{[dx]}{[dt]}=L\cdot T^{-1}\). La vitesse s’exprime donc en \(\text{m}\cdot\text{s}^{-1}\). Connaissant la fonction \(v_x(t)\), on peut remonter à \(x(t)\) par l’opération mathématique inverse de la dérivée : on dira que la position est la primitive de la vitesse .

Application 2.2: Un train se déplace en ligne droite à vitesse constante \(v_x(t)=v_0\). Exprimer la distance parcourue par le train au bout d’un temps \(T\).

Le train se déplace à vitesse constante: \(v_{x}(t)=\frac{dx}{dt}=v_0\). Donc:

\[x(t) = v_{0} t + c\]

où \(c\) est une constante. Si l’on suppose que à l’instant \(t=0\) on a \(x(t=0)=0\), alors on peut déduire que \(c=0\).

La distance parcourue au bout d’un temps \(t\) est donc:

\[\boxed{x(T)=v_0 T}\]

Le calcul différentiel, sur lequel repose toute la physique contemporaine, a été développé indépendamment par Newton (1642-1727) et Leibniz (1646-1716). Nous rappelons dans ce complément les définitions de dérivée et de primitive d’une fonction.

Dérivée et équation de la tangente

Pour définir la dérivée d’une fonction \(f(t)\), on considère deux points \(t_0\) et \(t_0+ \Delta t\) très proches l’un de l’autre, comme illustré sur la fig-ch2-derivee.

On note \(\Delta f = f(t_0+ \Delta t) - f(t_0)\) la variation de la fonction \(f\). On définit alors la dérivée de \(f\) en \(t_0\) comme la limite du taux de variation :

()\[f'(t_0) = \frac{df }{dt} \bigg\vert_{t_0} = \lim_{\Delta t \to 0} \frac{\Delta f}{\Delta t} \ .\]

Avertissement

Suivant les disciplines, on rencontre différentes notations pour désigner la dérivée. La première notation de l’équation () est employée traditionnellement en mathématiques, alors que le seconde est plus commune en physique.L’intérêt de la seconde notation est qu’elle exprime la dérivée comme le rapport de deux quantités infinitésimales.

Rappelons encore l’interprétation géométrique de la dérivée qui correspond à la pente de la tangente à la courbe. Elle représente le taux de variation de la courbe en chaque point. L’équation de la tangente \(y(t)\) à la courbe représentative de la fonction \(f\) au point \(t_0\) est donnée par :

\[y(t) = f(t_0) + \frac{d f}{dt}\bigg\vert_{t_0}(t-t_0) \ .\]

Dérivée d’une fonction composée

Les fonctions rencontrées en physique sont très souvent des fonctions composées : \(\cos \omega t\), \(e^{-\alpha t}\), \(\ln \sqrt{1-t^2}\), … Pour dériver une fonction de la forme \(f\left( u(t) \right)\), on applique la règle suivante [1] :

\[\frac{d f}{dt} = \frac{ df}{du} \frac{du}{dt} \ .\]

On a par exemple : \(d (\cos \omega t)/dt=-\omega \sin \omega t\), ou encore : \(d (e^{-\alpha t})/dt=-\alpha e^{-\alpha t}\).

La table ci-dessous rappelle quelques dérivées de fonctions usuelles.

Dérivées de fonctions usuelles

Fonction \(f\)	Dérivée \(f'\)	Intervalles de dérivabilité
k (constante)	0	\(\mathbb{R}\)
\(x\)	1	\(\mathbb{R}\)
\(a x + b\)	\(a\)	\(\mathbb{R}\)
\(x^n (n \in \mathbb{N})\)	\(n x^{n-1}\)	\(\mathbb{R}\)
\(x^{-n} (n \in \mathbb{N})\)	\(-n x^{-n-1}\)	\([-\infty;0[ ]0;+\infty]\)
\(\cos{x}\)	\(-\sin{x}\)	\(\mathbb{R}\)
\(\sin{x}\)	\(\cos{x}\)	\(\mathbb{R}\)
\(\tan{x}\)	\(\frac{1}{\cos^2{x}}=1+\tan^2{x}\)	\(\mathbb{R}\)
\(e^{x}\)	\(e^{x}\)	\(\mathbb{R}\)
\(\ln{x}\)	\(\frac{1}{x}\)	\(]0;+\infty]\)

Primitive

En physique, nous sommes fréquemment appelés à utiliser l’opération inverse de la dérivation. On appelle primitive de la fonction \(f\) toute fonction \(F\) telle que :

\[\frac{dF}{dt} = f(t) \ .\]

Avertissement

Cette définition implique que, contrairement à la dérivation, la primitive d’une fonction n’est pas unique : comme la dérivée d’une constante est nulle, si on ajoute n’importe quelle constante \(C\in \mathbb{R}\) à \(F\), la fonction obtenue est encore une primitive de \(f\): \(d (F(t) + C)/ dt = d F / d t + 0 = f(t)\).

Par conséquent, une primitive est toujours définie à une constante près.

On a par exemple : \(f(t)=\cos t \ \Rightarrow \ F(t)= \sin t + C\), ou encore : \(f(t)=t \ \Rightarrow \ F(t)=\frac{t^2}{2}+C\).

La table ci-dessous rappelle quelques primitives de fonctions usuelles.

Primitives de fonctions usuelles

Fonction \(f\)	Intervalles	Primitive \(F\)
\(k\) (constante)	\(\mathbb{R}\)	\(kx+C\)
\(x\)	\(\mathbb{R}\)	\(\frac{x^2}{2}+C\)
\(x^n (n \in \mathbb{N}^{*})\)	\(\mathbb{R}\)	\(\frac{x^{n+1}}{n+1}+C\)
\(x^{-n} (n \in \mathbb{N} ; n\ge2)\)	\([-\infty;0[ ]0;+\infty]\)	\(-\frac{1}{n-1} x^{1-n} + C\)
\(\cos{x}\)	\(\mathbb{R}\)	\(\sin{x}+C\)
\(\sin{x}\)	\(\mathbb{R}\)	\(-\cos{x}+C\)
\(\exp{x}\)	\(\mathbb{R}\)	\(\exp{x}+C\)
\(\ln{x}\)	\(\mathbb{R}^{*}_{+}\)	\(x\ln{x}-x+C\)

La vitesse étant elle-même une fonction du temps, on introduit la notion d’ accélération pour quantifier ses variations. L’accélération est définie comme la dérivée de la vitesse par rapport au temps :

()\[\boxed{a_x(t) = \frac{d v_x}{d t} = \frac{d^2 x}{d t^2} \ .}\]

L’accélération correspond également à la dérivée seconde de la position. Dans le système international, elle s’exprime en \(\text{m}\cdot\text{s}^{-2}\). Il est important de noter que l’accélération peut prendre des valeurs aussi bien positives que négatives : \(a_x>0\) en phase d’accélération (lorsque la vitesse augmente), et \(a_x<0\) en phase de décélération (lorsque la vitesse diminue). Si la vitesse est constante, l’accélération est nulle : on parle alors de mouvement rectiligne uniforme.

Application 2.3: On lâche un ballon sans vitesse initiale à l’instant \(t=t_0\) en \(x=0\). L’axe \((Ox)\) est vertical, orienté vers le bas. On observe alors que la position évolue en fonction selon la loi: \(x(t) = \frac{1}{2}g(t-t_0)^2\), avec \(g\approx 9.81~\text{m}\cdot\text{s}^{-2}\) l’accélération de la pesanteur. a) Établir l’expression de la vitesse \(v_x(t)\). b) En déduire que l’accélération \(a_x(t)\) est constante.

1. La vitesse est par définition la dérivée de la position en fonction du temps:

\[v_x(t)=\frac{dx}{dt}=g(t-t_0)\]

2. L’accélération est par définition la dérivée de la vitesse en fonction du temps:

\[a_x(t)=\frac{dv}{dt}=g\]

L’accélération est donc constante.

Un mouvement pour lequel l’accélération est constante est dit uniformément accéléré.

Généralisation à 3 dimensions

Dans le cas général d’un mouvement dans l’espace (c’est-à-dire à 3 dimensions), la position du point \(M\) à l’instant \(t\) est repérée par le vecteur position \(\vec{r} = \overrightarrow{OM}\). Les vecteurs vitesse \(\vec{v}(t)\) et accélération \(\vec{a}(t)\) sont alors définis par :

()\[\boxed{\vec{v}(t) = \frac{d \vec{r}}{d t} \ , \quad \text{et} \quad \vec{a}(t) = \frac{d \vec{v}}{d t} \ .}\]

En coordonnées cartésiennes, on a donc :

\[\begin{split}\vec{r}(t) = \begin{pmatrix} x(t) \\ y(t) \\ z(t) \end{pmatrix} \ , \quad \vec{v}(t) = \begin{pmatrix} \displaystyle{d x/d t} \\ \displaystyle{d y/d t} \\ \displaystyle{d z/d t} \end{pmatrix} \ , \quad \text{et} \quad \vec{a}(t) = \begin{pmatrix} \displaystyle{d v_x/d t} \\ \displaystyle{d v_y/d t} \\ \displaystyle{d v_z/d t} \end{pmatrix} \ ,\end{split}\]

où \(x\), \(y\) et \(z\) sont respectivement l’abscisse, l’ordonnée et l’altitude du point \(M\).

La fig-ch2-vitesse permet de mieux comprendre ces définitions. Discutons tout d’abord le vecteur vitesse. On note \(M\) et \(M'\) les positions du point dont on suit la trajectoire à deux instants infiniment proches \(t\) et \(t+\Delta t\). Pendant cet intervalle de temps, le vecteur position varie de la quantité infinitésimale \(\Delta \vec{r} = \vec{r}(t+\Delta t)-\vec{r}(t)\). Dans la limite \(\Delta t \to 0\), le point \(M'\) se rapproche de plus en plus du point \(M\) de telle sorte que \(\Delta \vec{r} \to \vec{0}\). Le rapport \(\Delta \vec{r} / \Delta t\) tend quant à lui vers une valeur finie qui définie le vecteur vitesse \(\vec{v}\) :

\[\vec{v} = \lim_{\Delta t \to 0} \frac{\Delta \vec{r}}{\Delta t} = \frac{d \vec{r}}{d t} \ .\]

Nous pouvons en particulier conclure que le vecteur vitesse est tangent à la trajectoire.

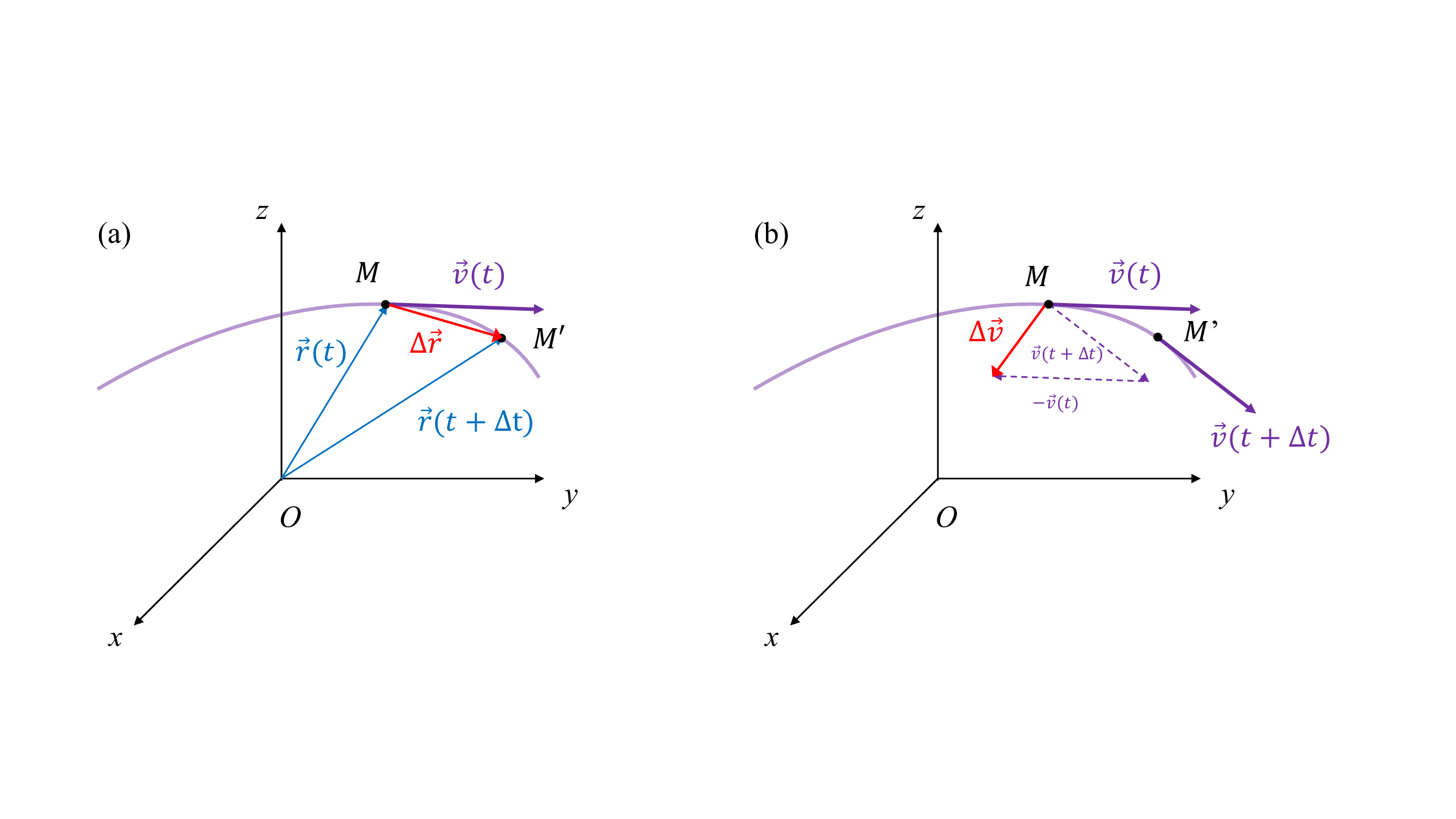
Définition et interprétation géométrique des vecteurs vitesse (a) et accélération (b).

Un raisonnement similaire peut être développé pour le vecteur accélération. Pendant le même intervalle de temps \(\Delta t\), le vecteur vitesse varie de la quantité \(\Delta \vec{v}= \vec{v}(t+\Delta t) -\vec{v} (t)\), comme représenté sur la figure 1.3(b). Dans la limite \(\Delta t \to 0\), le rapport \(\Delta \vec{v}/ \Delta t\) tend également vers une valeur finie :

\[\vec{a} = \lim_{\Delta t \to 0} \frac{\Delta \vec{v}}{\Delta t} = \frac{d \vec{v}}{d t} \ .\]

La figure 1.3(b) révèle également que le vecteur accélération est toujours orienté vers l’intérieur de la concavité de la trajectoire.

Natures d’un mouvement

On distingue trois types de mouvements :

• les mouvements uniformes, pour lesquels la norme du vecteur vitesse est constante.

• les mouvement accélérés, pour lesquels la vitesse augmente.

• les mouvements décélérés, pour lesquels la vitesse diminue.

Mathématiquement, la norme du vecteur vitesse est définie par :

\[v=\Vert \vec{v} \Vert = \sqrt{v_x(t)^2+v_y(t)^2+v_z(t)^2} \ ,\]

de telle sorte que :

()\[\frac{ d v}{d t}= \frac{\vec{a}\cdot\vec{v}}{v} \ .\]

Cette dernière relation indique que le signe de la dérivée de la vitesse est le même que celui du produit scalaire \(\vec{a}\cdot\vec{v}\) (car \(v \geq 0\) par définition de la norme). Nous pouvons en conclure que :

• si \(\vec{a}\cdot\vec{v}=0\) alors le mouvement est uniforme.

• si \(\vec{a}\cdot\vec{v}>0\) alors le mouvement est accéléré.

• si \(\vec{a}\cdot\vec{v}<0\) alors le mouvement est décéléré.

Pour qu’un mouvement soit uniforme, il faut donc que l’une des conditions suivantes soit vérifiée : soit \(\vec{a}=\vec{0}\), auquel cas le mouvement est rectiligne (cf. § Mouvement unidimensionnel), soit \(\vec{a} \perp \vec{v}\), ce qui correspond à un mouvement circulaire (cf. § Mouvement circulaire).

Mouvement circulaire

Nous discutons maintenant les mouvements dans le plan \(Oxy\) qui sont tels que : \(\Vert \vec{r} \Vert = R\), où \(R\) est une constante positive. Les trajectoires correspondantes sont des cercles de rayon \(R\), centrés à l’origine.

Position et angle polaire

Dans le cas d’un mouvement circulaire, la position du point \(M\) est spécifiée de façon unique par l’angle orienté \(\varphi = (\widehat{\vec{e}_x,\vec{r}})\) — voir la fig-ch2-mouvcirc.

\(\varphi\) est appelé l’angle polaire. Les coordonnées du point \(M\) peuvent s’exprimer de la façon suivante :

()\[\begin{split}\begin{cases} x(t) = R \cos \varphi (t) \ , \\ y(t) = R\sin \varphi (t) \ . \end{cases} \label{coords}\end{split}\]

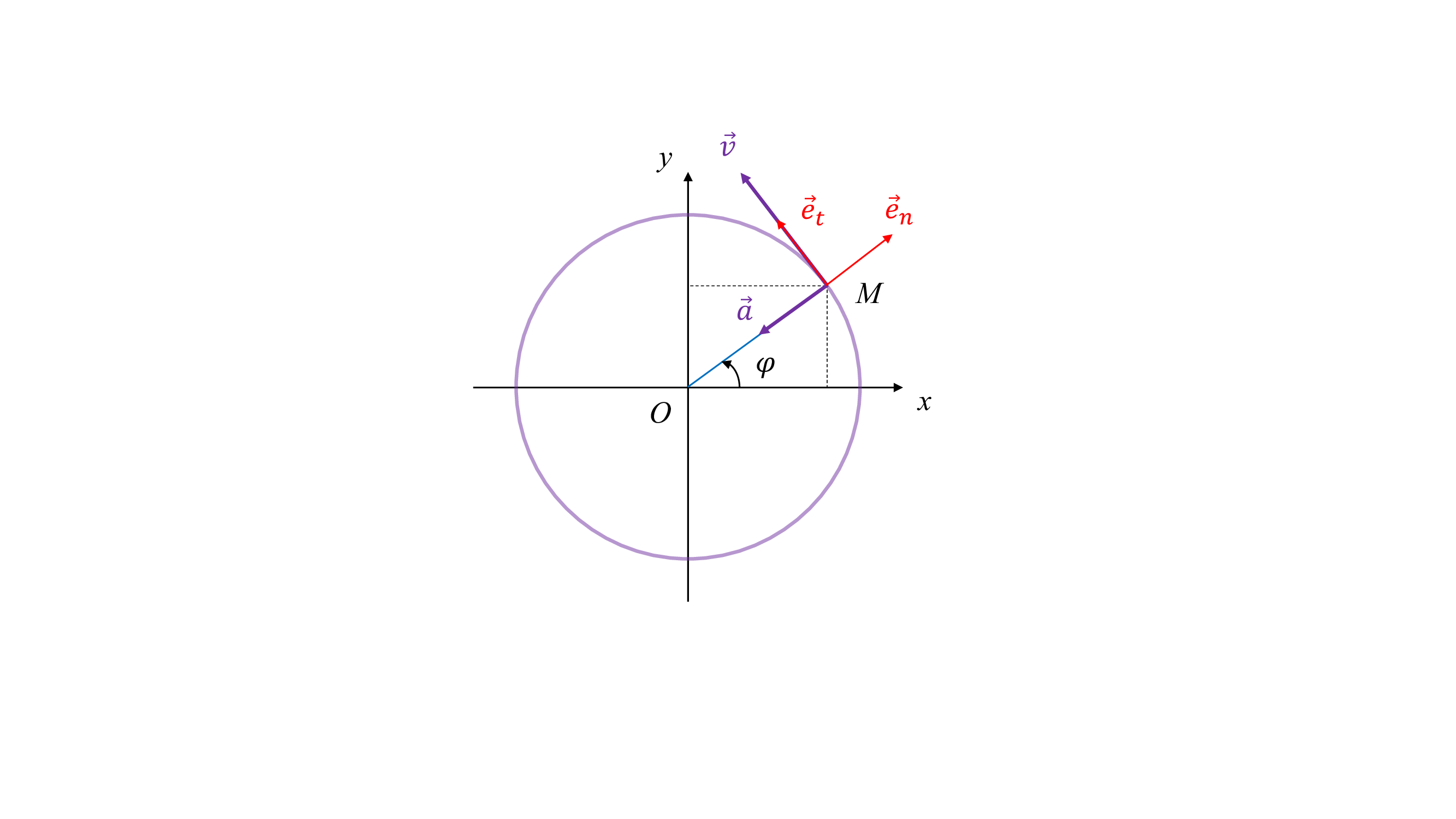
Mouvement circulaire dans le plan \(Oxy\). Les vecteurs unitaires \(\vec{e}_n\) et \(\vec{e}_t\) sont respectivement perpendiculaire et tangent au cercle de rayon \(R\). Sur ce schéma, le point \(M\) se déplace dans le sens trigonométrique.

On définit alors deux nouveaux vecteurs unitaires : le vecteur \(\vec{e}_n=\vec{r}/R\) qui est perpendiculaire à la trajectoire, et le vecteur \(\vec{e}_t\) qui est tangent à la trajectoire. Un peu de géométrie permet de déterminer les coordonnées dans la base cartésienne de ces vecteurs :

()\[\begin{split}\vec{e}_n = \begin{pmatrix} \cos \varphi \\ \sin \varphi \end{pmatrix} \ , \quad \text{et} \quad \vec{e}_t = \begin{pmatrix} - \sin \varphi \\ \cos \varphi \end{pmatrix} \ .\end{split}\]

Contrairement aux vecteurs de la base cartésienne qui sont fixes, les vecteurs \(\vec{e}_n\) et \(\vec{e}_t\) sont mobiles : leurs coordonnées évoluent à mesure que le point \(M\) se déplace.

Application 2.5: On considère le mouvement circulaire défini par les équations horaires (Eq. ()). a) Vérifier que : \(x(t)^2 + y(t)^2 =R^2\). b) Montrer également que les vecteurs \(\vec{e}_n\) et \(\vec{e}_t\) sont unitaires et orthogonaux.

1. Les équations horaires sont:

\[\begin{split}\begin{cases} x(t) = R \cos \varphi (t) \ , \\ y(t) = R\sin \varphi (t) \ . \end{cases}\end{split}\]

donc:

\[\begin{split}x^2+y^2 &= R^2 \cos^2{\varphi (t)} + R^2 \sin^2{\varphi (t)} \\ &= R^2 \big(\underbrace{\cos^2{\varphi (t)} + \sin^2{\varphi (t)}}_{=1}\big) \\ &= R^2\end{split}\]

2. Les vecteurs \(\vec{e}_n\) et \(\vec{e}_t\) sont définis par:

\[\begin{split}\vec{e}_n = \begin{pmatrix} \cos \varphi \\ \sin \varphi \end{pmatrix} \ , \quad \text{et} \quad \vec{e}_t = \begin{pmatrix} - \sin \varphi \\ \cos \varphi \end{pmatrix} \ .\end{split}\]

Donc, par définition de la norme d’un vecteur:

\[\begin{split}\Vert \vec{e}_{n} \Vert = \cos^2{\varphi (t)} + \sin^2{\varphi (t)} = 1 \\ \Vert \vec{e}_{t} \Vert = (-\sin{\varphi (t)})^2 + \cos^2{\varphi (t)} = \sin^2{\varphi (t)} + \cos^2{\varphi (t)} = 1\end{split}\]

Pour démontrer qu’ils sont orthogonaux, nous allons utiliser le produide scalaire. En effet le produit scalaire de deux vecteurs orthogonaux est nul.

\[\vec{e}_{n} \cdot \vec{e}_{t} = \cos{\varphi} \times (-\sin{\varphi}) + \sin{\varphi} \times \cos{\varphi} = 0\]

Le produit est bien nul et donc les deux vecteurs sont orthogonaux.

Mouvement circulaire uniforme

Un cas particulier important est celui du mouvement circulaire uniforme : supposons que l’angle \(\varphi\) varie au cours du temps selon la loi \(\varphi(t) = \omega t\), où \(\omega>0\) est la vitesse angulaire. Dans ce cas, le point \(M\) revient à sa position de départ au bout d’un intervalle de temps \(T\) tel que [2] :

()\[\begin{split}\begin{cases} x(t+T) = x(t) \\ y(t+T) = y(t) \end{cases} \quad \Rightarrow \quad \boxed{T=\frac{2\pi}{\omega} \ .}\end{split}\]

\(T\) est la période du mouvement, et \(\omega\) est aussi appelée la pulsation. L’unité SI de la pulsation est le \(\text{rad} \cdot \text{s}^{-1}\). On définit également la fréquence \(f=1/T\), qui s’exprime en Hz (ou en tours par minute). Fréquence et pulsation sont reliées par l’égalité :

\[\boxed{\omega = 2 \pi f \ .}\]

La vitesse s’obtient alors en dérivant les coordonnées (Equation ()) du point \(M\) en tenant compte de la relation \(\varphi(t)=\omega t\) :

()\[v_x(t) = \frac{d x}{d t} = -R \omega \sin \omega t \ , \quad \text{et} \quad v_y(t) = \frac{d y}{d t} = R \omega \cos \omega t \ .\]

La norme \(v=\Vert \vec{v} \Vert\) du vecteur vitesse s’en déduit directement :

\[v = \sqrt{v_x^2 + v_y^2} = R\omega \ .\]

La norme de la vitesse étant constante, le mouvement est bien uniforme. En outre, si l’on compare l’équation () avec l’expression () des vecteurs unitaires, on peut encore écrire :

\[\boxed{\vec{v} = v \vec{e}_t \ .}\]

Autrement dit, le vecteur vitesse est tangent à la trajectoire.

En dérivant encore une fois par rapport au temps, on détermine les composantes du vecteur accélération :

\[a_x(t) = \frac{d v_x}{d t} = -R \omega^2 \cos \omega t \ , \quad \text{et} \quad a_y(t) = \frac{d v_y}{d t} = -R \omega^2 \sin \omega t \ .\]

La norme \(a=\Vert \vec{a} \Vert\) du vecteur accélération est alors donnée par :

\[a = \sqrt{a_x^2 + a_y^2} = R\omega^2 \ .\]

On obtient donc une relation entre vitesse et accélération pour un mouvement circulaire uniforme :

()\[\boxed{a = \frac{v^2}{R} \ .}\]

Finalement, on note que le vecteur accélération est perpendiculaire au cercle :

\[\boxed{\vec{a} = - a \vec{e}_n \ .}\]

L’accélération étant dirigée vers l’intérieur du cercle, on dira qu’elle est centripète.

La centrifugeuse du CEA-Cesta au Barp (crédit photo : CEA).

Application 2.5: Afin de sonder les propriétés de la matière en condition extrême, le Centre d’Etudes Scientifiques et Techniques d’Aquitaine (Cesta) du CEA est équipé d’une centrifugeuse (ch2-centrifugeuse ). L’échantillon est placé dans une nacelle située à 8.4m de l’axe de rotation. Le système est mis en rotation à vitesse angulaire constante \(\omega = 100\) tours/min. Calculer l’accélération subie par l’échantillon. On exprimera le résultat en « nombre de \(g\) », où \(g\) est l’accélération de la pesanteur (\(g\approx 9,81~\text{m}\cdot\text{s}^{-2}\)).

Nous avons vu ci-dessus que l’accélération pour un mouvement circulaire peut s’écrire: \(a=R\cdot \omega^2\).

Pour l’application numérique, exprimons \(\omega\) en unité standard, c’est à dire en radian par seconde. Comme 1 tour vaut \(2\pi\) radians et 1min=60s, on a \(\omega=\frac{100\times2\pi}{60}\approx10.46 rad\cdots^{-1}\).

L’accélération vaut donc:

\[a=R \omega^2=8.4\times(10.46)^2 \approx 920.23 m\cdot.s^{-2}\]

Comme \(g\approx 9,81~\text{m}\cdot\text{s}^{-2}\), on peut donc déduire que:

\[a=\frac{920.23}{9.81}\approx93.8 g\]

Mouvement circulaire non uniforme

Reprenons le raisonnement précédent dans le cas général où la vitesse angulaire \(d \varphi / dt\) n’est pas constante. En dérivant les coordonnées (Eq. ()) du vecteur position par rapport au temps, on obtient :

()\[\vec{v} = -R \frac{d \varphi}{dt} \sin \varphi(t) \vec{e}_x + R \frac{d \varphi}{dt} \cos \varphi(t) \vec{e}_y \ .\]

Ceci s’exprime encore dans la base locale \((\vec{e}_n,\vec{e}_t)\) :

()\[\boxed{\vec{v} = R \frac{d \varphi}{dt} \vec{e}_t \ .}\]

Bien entendu, on trouve que le vecteur vitesse est toujours tangent à la trajectoire. Si l’on dérive encore une fois l’équation (), on obtient l’expression de l’accélération qui prend la forme suivante dans la base locale :

()\[\vec{a} = -R \left( \frac{d \varphi}{dt} \right)^2 \vec{e}_n + R \frac{d^2 \varphi}{dt^2} \vec{e}_t \ .\]

On voit donc que l’accélération a maintenant une composante tangentielle qui est proportionnelle à l’accélération angulaire \(d^2 \varphi/ dt^2\). On peut encore écrire en fonction de \(v=\Vert \vec{v} \Vert\) :

()\[\boxed{\vec{a} = -\frac{v^2}{R} \vec{e}_n + R \frac{d^2 \varphi}{dt^2} \vec{e}_t \ .}\]

Démontrer les équations () et (). Commenter le résultat dans le cas où la vitesse angulaire est constante.

\[\begin{split}\vec{v} &= \frac{d\varphi}{dt} \vec{e}_{t} \Rightarrow v^2 = R^2 \big(\frac{d\varphi}{dt}\big)^2 \\ \vec{a} &= \frac{d\vec{v}}{dt} = \frac{d}{dt}\Big(-R \frac{d\varphi}{dt} \sin{\varphi} \vec{e}_x + R \frac{d\varphi}{dt} \cos{\varphi} \vec{e}_y\Big) \\ &= -R \frac{d^2\varphi}{dt^2} \sin{\varphi} \vec{e}_x - R \Big(\frac{d\varphi}{dt}\Big)^2 \cos{\varphi}\vec{e}_x + R \frac{d^2\varphi}{dt^2} \cos{\varphi} \vec{e}_y - R \Big(\frac{d\varphi}{dt}\Big)^2 \sin{\varphi} \vec{e}_y &= R \frac{d^2\varphi}{dt^2} \underbrace{\Big[\sin{\varphi}\vec{e}_x + \cos{\varphi}\vec{e}_y\Big]}_{\vec{e}_t} - R\Big(\frac{d\varphi}{dt}\Big)^2 \underbrace{\Big[\cos{\varphi} \vec{e}_x + \sin{\varphi} \vec{e}_y \Big]}_{\vec{e}_n}\end{split}\]

soit finalement:

\[\boxed{\vec{a} = R \frac{d^2\varphi}{dt^2} \vec{e}_t - R \Big(\frac{d\varphi}{dt}\Big)^2 \vec{e}_{n}}\]

or on note que: \(\Big(\frac{d\varphi}{dt}\Big)^2=\frac{v^2}{R^2}\). Et donc finalement:

\[\boxed{\vec{a}=-\frac{v^2}{R^2}\vec{e}_{n} + R \frac{d^2\varphi}{dt^2} \vec{e}_{t}}\]

Lorsque \(\omega=\frac{d\varphi}{dt}=\text{cte}\), alors:

\[\begin{split}\vec{v} &= R\omega \vec{e}_t \\ \vec{a} &= -R \omega^2 \vec{e}_n\end{split}\]

et l’on retrouve bien les résultats du mouvement circulaire uniforme.

[1]

Avec les notations des mathématiciens, la dérivée de la fonction composée \(f \circ u (t)\) est : \(\left( f' \circ u(t)\right) \times u'(t)\).

[2]

Le système d’équation () admet une infinité de solutions définies à \(2\pi\) près. La période \(T\) est le plus petite solution positive.