9. Capillarité

Dans ce chapitre, nous étudions les phénomènes d’interaction qui se produisent aux interfaces liquides. Les effets capillaires interviennent dans de nombreux processus de la vie quotidienne (forme des gouttes, imbibition d’un morceau de sucre, …) ou en lien avec le vivant (dynamique des alvéoles pulmonaires). Ils sont également utilisés en nanotechnologies pour la conception de nouveaux matériaux.

Un peu d’Histoire…

Bien que longtemps inexpliqué, le phénomène de capillarité a été observé et décrit il y a plusieurs siècles. Leonard de Vinci fait mention en 1490 de la montée de liquide dans des tubes capillaires de différents diamètres, sans fournir d’explication. Il fallu attendre les travaux du médecin anglais James Jurin qui développa et confirma les travaux réalisés par ses prédécesseurs, en particulier Francis Hauksbee et Isaac Newton.

Définition de la tension de surface

Un expérience préliminaire

Commençons par une expérience simple : prenons un récipient rempli d’eau et agitons avec un batteur. On observe alors l’apparition de bulles d’air dans l’eau, et donc la création d’interfaces entre les phases liquides et gazeuses. Cette expérience illustre le fait qu’une interfaces entre un liquide et un gaz a une énergie : l’expérimentateur doit fournir de l’énergie mécanique pour créer des interfaces.

On remarque également que les bulles disparaissent très rapidement. Or si l’on ajoute quelques gouttes de liquide vaisselle, il est plus facile de créer des bulles dont la durée de vie est également plus longue. Les molécules de liquide vaisselle permettent donc de diminuer l’énergie de surface.

Gauche: Interactions entre molécules dans le volume du liquide et au voisinage d’une interface. Droite: Forme d’une goutte d’eau et de lait en apesanteur dans l’ISS (crédits photos : CNES).

La tension de surface : une énergie par unité de surface

Pour comprendre l’origine de cette énergie de surface, considérons une molécule dans le volume du liquide, comme la molécule \(a\) sur la ch9_fig_interaction (a). Cette molécule interagit en moyenne avec 6 molécules voisines. Ces interactions sont attractives puisque les interactions au sein d’un liquide sont cohésives. En revanche, pour une molécule au voisinage de la surface telle que la molécule \(b\) sur la ch9_fig_interaction (a), il n’y a — par construction — que 4 interactions attractives en raison de la présence de l’interface : il y a donc un déficit d’interactions attractives.

Si on note \(U_0\) l’ordre de grandeur de l’énergie potentielle d’interaction entre deux molécules (pour les liquides usuels \(U_0 \approx k_b T\)), alors pour une molécule en surface la pénalité énergétique est égale à \((6-4) \times U_0 = 2 U_0\). On définit alors l’énergie par unité de surface — appelée tension de surface ou tension de superficielle \(\gamma\) — qui est égale au coût énergétique \(\sim 2 U_0\) divisée par la surface \(S\sim d^2\) avec \(d\) la taille typique de la molécule :

()\[\gamma \approx \frac{2 U_0}{d^2}  \ .\]

D’après la formule (), la tension de surface est donc égale en ordre de grandeur à l’énergie typique d’interaction entre molécules divisée par l’échelle moléculaire \(d\) au carré. La tension de surface s’exprime donc en \(\text{J}\cdot\text{m}^2\). Le tableau suivant donne quelques valeurs (approximatives) de \(\gamma\) à température ambiante.

Interface	Tension de surface (\(\text{mN}\cdot \text{m}^{-1}\))
eau / air	72
eau savonneuse / air	20 – 30
eau / huile	50
mercure / air	485

Application 9.2: Sachant que pour les liquides usuels on a \(U_0 \approx k_B T\), avec \(T=300\) \(K\) et \(k_B =1,38 \times 10^{-23}~\text{J}\cdot\text{K}^{-1}\), estimez l’ordre de grandeur de \(\gamma\) (on prendra : \(d \approx 0,1~\text{nm}\)).

L’équation () nous donne: \(\gamma=\frac{2U_0}{d^2}\), avec:

\[\begin{split}U_0&\approx k_B T \\ &\approx1.38\times10^{-23}\times30 \\ &= 4\times10^{-21} J\end{split}\]

Comme \(d=0.1 \text{nm} =10^{-10} \text{m}\):

\[\gamma=\frac{2.4\times10^{-21}}{(10^{-10})^2}=0.8 J/m^2\]

Ainsi, pour un liquide de tension de surface \(\gamma\) et ayant une surface de contact \(S\) avec l’air, l’énergie de surface totale s’écrit :

()\[\boxed{ E_{s}= \gamma . S}\]

Pour diminuer l’énergie de surface, il faut donc soit diminuer la tension de surface (en ajoutant des molécules de savon par exemple), soit diminuer la surface \(S\). En particulier, la forme d’une goutte ou d’une bulle résulte de la minimisation de son énergie totale. En l’absence de gravité, seule l’énergie de surface est pertinente : cela revient à minimiser la surface de la goutte à volume fixé. Or, la forme géométrique qui possède la surface minimale pour un volume donné est la sphère : la forme des gouttes en apesanteur est donc sphérique — voir la ch9_fig_interaction (b).

Application 9.2: Estimer en Joule l’énergie de surface d’une goutte d’eau sphérique de 1 mm de rayon en contact avec l’air (\(\gamma = 72~\text{mN}\cdot \text{m}^{-1})\))

\[\begin{split}E_s &= \gamma \times \underbrace{4\pi R^2}_{=\text{Surface de la sphère}} \\ &= 72.8\times10^{-3} \times 4\pi 10^{-6} \\ &= 9\times10^{-7} \text{J}\end{split}\]

La tension de surface : une force par unité de longueur

Par analyse dimensionnelle, on peut remarquer que l’unité de \(\gamma\) vérifie la relation :

\[1~\text{J}\cdot \text{m}^{-2} = 1~\text{N} \cdot \text{m}^{-1} \ .\]

La tension de surface s’interprète donc comme une force par unité de longueur. Expérimentalement, on peut visualiser cette force en réalisant l’expérience décrite sur la ch9_fig_force1: un film de savon est initialement séparé en deux par une tige mobile. Si on perce à l’aide d’une aiguille le film de la partie gauche, la tige est alors tirée vers la droite par le film de savon restant. Pour un déplacement élémentaire de la tige, on peut écrire :

\[dE_{s}= \gamma \cdot dS = 2 \gamma L dx = Fdx \quad \Rightarrow \quad \boxed{F= 2\gamma L \ .}\]

Le facteur 2 correspond ici au fait qu’il y ait 2 interfaces eau-air (dessus et dessous). On retiendra que la tension de surface est la force par unité de longueur qui s’exerce parallèlement à l’interface, et dirigée du solide vers le liquide. Cette force tire le long de l’interface pour diminuer l’aire de contact entre le liquide et l’air.

La tension de surface est également une force par unité de longueur. Voir la vidéo de l’expérience sur Moodle.

Notion de Mouillage

Les différents types de mouillage

Considérons maintenant le cas d’une goutte posée sur un solide. Comme le montre la ch9_fig_mouillage2, une goutte d’huile posée sur du téflon a tendance à s’étaler, alors que la goutte d’eau ne s’étale presque pas. Ceci vient du fait que l’on peut généraliser la notion de tension de surface dès lors que deux phases quelconques non miscibles — solide, liquide ou gaz — sont en contact. La forme des gouttes est alors donnée par l’équilibre mécanique entre les 3 tensions interfaciales.

Gauche : Forme de gouttes posées sur une surface de téflon. Droite : Angle de contact.

On définit alors l’angle de contact \(\theta\) entre les interfaces liquide/air et liquide/solide, comme représenté sur la ch9_fig_mouillage2. Suivant la valeur de \(\theta\), on peut distinguer différentes configurations :

• le cas non mouillant, pour \(\theta > 90^{\circ}\), qui correspond à la situation A de la ch9_fig_mouillage.

• le cas mouillant, pour \(\theta < 90^{\circ}\), qui correspond à la situation B de la ch9_fig_mouillage.

• si \(\theta=0^{\circ}\), on parle de mouillage total. On dira que le liquide est parfaitement mouillant.

Différents types de mouillage. A : cas non mouillant. B: cas mouillant.

Loi de Young-Dupré

Pour déterminer l’angle de contact, considérons le schéma de droite de la ch9_fig_mouillage2. En effectuant la projection des forces interfaciales (par unité de longueur) selon l’axe \(x\), on obtient à l’équilibre :

()\[0=\gamma_{L/G} \cos{\theta}+\gamma_{S/L}-\gamma_{S/G}\]

On en déduit donc la loi de Young-Dupré qui permet de calculer l’angle de contact en fonction des différentes tensions interfaciales :

\[\cos{\theta}=\frac{\gamma_{S/G} - \gamma_{S/L}}{\gamma_{L/G}} \ .\]

Longueur capillaire

Comme le montre la ch9_fig_lcap, si on dépose un petit volume de liquide sur une surface, la goutte adopte une forme sphérique. Plus on augmente le volume déposé, plus les gouttes vont être aplaties par la gravité. La forme des gouttes découle donc d’une compétition entre énergie de surface et énergie potentielle de pesanteur.

Forme des gouttes en fonction du volume déposé (eau sur téflon).

Considérons en effet une goutte sphérique de rayon \(R\). Son énergie de surface est :

()\[E_S =\gamma \times 4 \pi R^2 \ ,\]

où \(\gamma = \gamma_{L/G}\). On peut également estimer l’énergie potentielle de pesanteur \(E_p\) de la goutte de rayon \(R\) :

\[E_p \approx m g R \ ,\]

avec \(m= \rho (4 \pi R^3)/3\). La goutte sera de forme sphérique si l’énergie de surface est grande devant l’énergie potentielle de pesanteur \(E_s \gg E_p\) :

\[\gamma 4 \times \pi R^2 \gg \rho \frac{4 \pi R^3}{3} g R \quad \Rightarrow \quad R \ll \sqrt{\frac{3\gamma}{\rho g}} \ .\]

On définit alors la longueur capillaire qui compare les effets de tension de surface et de gravité :

()\[\boxed{\ell_{c} = \sqrt{\frac{\gamma}{\rho g}} \ .}\]

Une goutte est de forme sphérique si \(R \ll \ell_{c}\) ; par contre, elle est aplatie par la gravité si \(R \gg \ell_{c}\).

Application 9.3: Calculer la longueur capillaire pour l’interface eau / air à température ambiante. Discuter la forme d’une goutte de rayon \(R=0.5\) mm.

\[\begin{split}\ell_{\rm cap}&=\sqrt{\frac{\gamma}{\rho g}} \\ &\approx\sqrt{\frac{72.8\times10^{-3}}{10^3\times9.81}} \\ &\approx2.7mm\end{split}\]

Donc \(R=0.5\ll \ell_{\rm cap}\), c’est la force de tension superficielle qui domine et donc la goutte aura la forme d’une calotte sphérique et ne sera pas applatie par la gravité.

Loi de Laplace et ascension capillaire

Loi de Laplace

Dans le Chapitre 8, nous avons montré que l’interface entre un liquide et un gaz dans un champ de gravité uniforme est horizontale. Et pourtant, l’expérience montre qu’une goutte ou qu’une bulle ont plutôt tendance à adopter une forme sphérique. En effet, les forces de tension de surface peuvent contrebalancer les forces de pression hydrostatique. Considérons en effet une goutte sphérique de rayon \(R\) et de tension de surface \(\gamma\). On peut montrer que la différence de pression entre l’intérieur et l’extérieur de la bulle obéit à la loi de Laplace :

()\[\boxed{\Delta p_{\textrm{goutte}}=p_{int}-p_{ext}= \frac{2 \gamma}{R}  .}\]

La pression au passage d’une interface est donc discontinue, la différence de pression étant proportionnelle à la tension de surface. La pression intérieure est plus élevée qu’à l’extérieur.

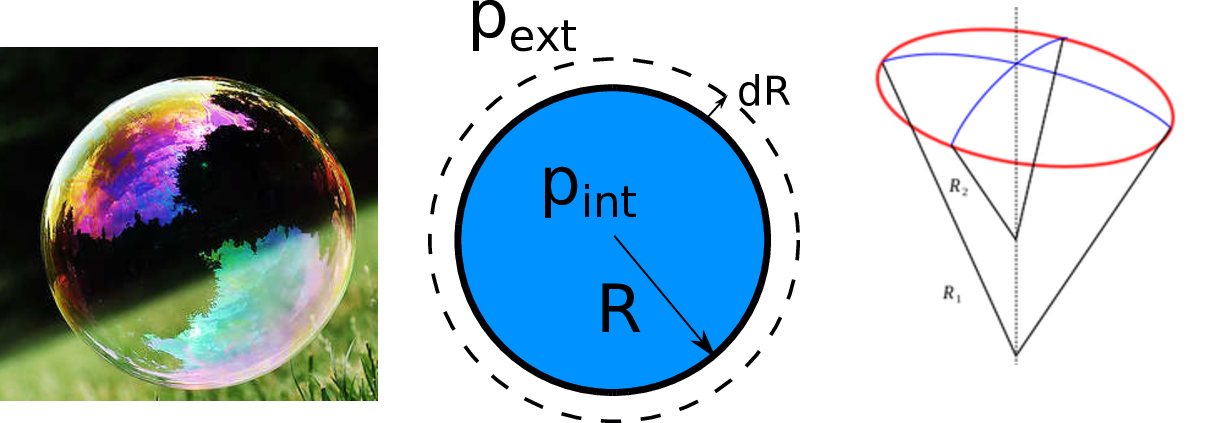
Surpression dans une bulle ou une goutte. À droite : définition des rayons de courbure.

Notons que dans le cas d’une bulle de savon, il y a 2 interfaces en contact avec l’air. La différence de pression entre l’intérieur de la bulle et l’extérieur est alors :

()\[\boxed{\Delta p_{\textrm{bulle}}=p_{int}-p_{ext}= \frac{4 \gamma}{R} \ .}\]

Application 9.4: Calculer la surpression à l’intérieur d’une bulle de savon de rayon \(R = 1~\text{cm}\).

\[\begin{split}p_{int}-p_{ext}&=\underbrace{2\times}_{\text{2 interfaces}}\frac{2\gamma}{R}\\ &=\frac{4\gamma}{R}\\ &=100\text{Pa}\end{split}\]

Démonstration et généralisation de la loi de Laplace

Faisons subir une transformation à cette bulle de savon en faisant passer son rayon de \(R\) à \(R+dR\) (voir ch9_laplace au milieu). Dans ce cas, son volume augmente de \(dV= 4 \pi R^2 dR\). La surface de la bulle a augmenté de \(dS=8 \pi R dR\). Le coût énergétique pour créer cette surface supplémentaire est \(dE_s= 2 \gamma dS\) (x2 car il y a deux interfaces). Le travail des forces de pression associées à \(P_{int}\) et \(P_{ext}\) va compenser la variation d’énergie de surface.

La force associée à une pression s’exprime comme \(F= P. S\) et le travail associé est : \(\delta W= \vec{F} . \vec{d \ell}= P.S d \ell\). On trouve donc :

\[- p_{ext} (4 \pi R^2) dR +p_{int} (4 \pi R^2) dR=2\gamma dS =\gamma 8 \pi R dR \ ,\]

d’où

\[p_{int} -p_{ext} =\frac{4 \gamma}{R} \ .\]

Dans le cas où l’interface n’est pas sphérique, il faut prendre en compte les rayons de courbures \(R_1\) et \(R_2\) de l’interface qui sont obtenus en prenant le rayon de courbure de l’interface dans 2 directions orthogonales (voir ch9_laplace de droite). Pour une goutte (une seule interface avec l’air), on trouve :

\[\boxed{p_{int} -p_{ext} =\gamma \left( \frac{1}{R_1}+\frac{1}{R_2} \right) \ .}\]

On peut remarquer que si \(R_1=R_2=R\) cas qui correspond au cas d’une sphère, on retrouve l’expression  ()) : \(\Delta p =\frac{2 \gamma}{R}\).

Ascension capillaire : Loi de Jurin

On s’intéresse dans cette partie à la formation d’un ménisque par un liquide dans un tube cylindrique de rayon \(R\). Comme le montre la ch9_jurin1, un liquide mouillant va monter d’autant plus que le rayon du tube est fin. Dans le cas d’un liquide non mouillant, on observe une dépression au lieu d’une ascension du liquide.

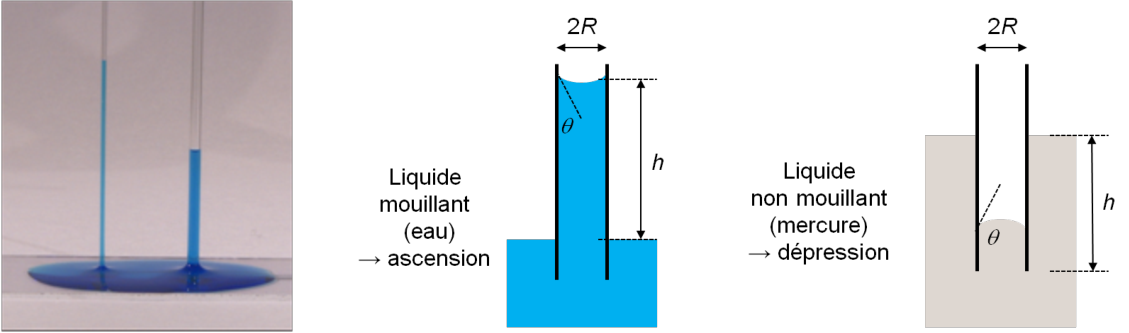
Ascension d’un liquide dans un tube capillaire.

Pour relier la hauteur d’ascension du liquide au rayon du tube, nous appliquons la loi de Laplace. Considérons la situation représentée sur la ch9_jurin3. La pression au point A (sous le ménisque) est donnée par :

\[p_{0} -p_{A} =\frac{2 \gamma}{R_c} \ ,\]

où \(R_c\) est le rayon du ménisque, supposé sphérique. Par construction géométrique, on a :

\[R_c = \frac{R}{\cos{\theta}} \ .\]

La pression au point B est donnée par la relation de l’hydrostatique :

\[p_{B}=p_{A} + \rho g h \ .\]

Par ailleurs, on a également \(p_B= p_C=p_0\), de telle sorte que l’on obtienne :

\[p_{B}-p_{A} =\rho g h=\frac{2 \gamma \cos{\theta}}{R} \ .\]

On démontre ainsi la loi de Jurin :

()\[\boxed{h=\frac{2 \gamma \cos{\theta}}{\rho g R} \ .}\]

Loi de Jurin.

Ainsi, si le liquide mouille les parois du tube (\(\theta >0\)), on trouve \(h >0\) : il y a ascension du liquide dans le tube. Plus le rayon \(R\) est fin, plus \(h\) augmente. Si le liquide ne mouille pas les parois du tube (\(\theta > 90^{\circ}\)) alors \(h<0\) : il y a dépression.

Application 9.5: Calculer la hauteur d’ascension de l’eau dans un tube en verre de rayon \(R=100\) \(\mu \text{m}\). On supposera que le liquide est parfaitement mouillant (\(\theta = 0^{\circ}\)).

Le liquide est parfaitement mouillant, et donc \(\theta = 0^{\circ}\). On a alors:

\[\begin{split}h&=\frac{2\gamma}{\rho g R}\\ &= \frac{2\times72.8\times10^{-3}}{10^{3}\times9.81\times100\times10{-6}}\\ &\approx 14.8cm\end{split}\]