8. Statique des fluides
Dans ce chapitre, nous appliquons les principes de la mécanique pour décrire les propriétés des fluides. Nous démontrons la loi de l’hydrostatique qui exprime la variation de pression avec l’altitude. Nous appliquons ensuite cette loi pour établir la formule de la poussée d’Archimède.
Équation d’état d’un fluide
Un fluide est un milieu matériel continu et déformable, qui possède la propriété de s’écouler. Il existe deux états fluides de la matière : les gaz et les liquides. Un liquide adopte la forme du récipient qui le contient ; il est limité par une interface. Un gaz occupe quant à lui tout le volume disponible.
On caractérise les fluides par leur compressibilité, c’est-à-dire leur capacité à changer de volume lorsqu’on exerce sur eux une contrainte.
Les liquides sont généralement très peu compressibles : leur masse volumique \(\rho\) est (quasiment) constante.
Contrairement aux liquides, les gaz ont une compressibilité finie.
Considérons par exemple \(n\) moles d’un gaz parfait contenu dans une enceinte de volume \(V\) et maintenu à la température \(T\). D’après la loi des gaz parfaits, la pression est donnée par : \(p=nRT/V\), où \(R=8.31~\text{J}\cdot\text{mol}^{-1}\cdot\text{K}^{-1}\). La masse \(m\) de gaz se déduit de la masse molaire \(M\) à partir de la relation : \(m=nM\). Sa masse volumique vérifie donc :
On peut alors ré-exprimer la loi des gaz parfaits sous la forme suivante :
Loi de l’hydrostatique
Forces de pression
Nous avons vu au Chapitre 7 qu’un fluide exerce des forces pressantes. Considérons le cas simple d’un fluide dont la pression \(p\) est constante. Le fluide est délimité par une paroi plane d’aire \(S\). On note \(\vec{n}\) le vecteur unitaire normal, dirigé vers l’extérieur. La force de pression exercée par le fluide sur la paroi est donnée par :
Pour illustrer cette notion, examinons la situation représentée sur la
ch8_magdebourg (a) : une enceinte est composée de
deux compartiments séparés par une paroi hermétique d’aire \(S\).
Les pressions dans chacun des compartiments sont notées \(p_{1}\) et
\(p_{2}\) (avec par exemple \(p_1>p_2\) pour fixer les idées).
Quelle est la résultante des forces pressantes qui s’exercent sur la
paroi ?
Compartiment de gauche : le fluide est à la pression \(p_1\) et le vecteur unitaire normal à la surface est \(\vec{n}_1=\vec{e}_x\). La force de pression est donc : \(\vec{F}_1 =p_1 S\, \vec{e}_x\).
Compartiment de droite : le fluide est à la pression \(p_2\) et le vecteur unitaire normal à la surface est \(\vec{n}_2=-\vec{e}_x\). La force de pression est donc : \(\vec{F}_2 =-p_2 S \, \vec{e}_x\).
La force totale qui s’exerce sur la paroi est donc :
Si la paroi est mobile et \(p_{1}>p_{2}\), alors la paroi se déplacera de la gauche vers la droite.
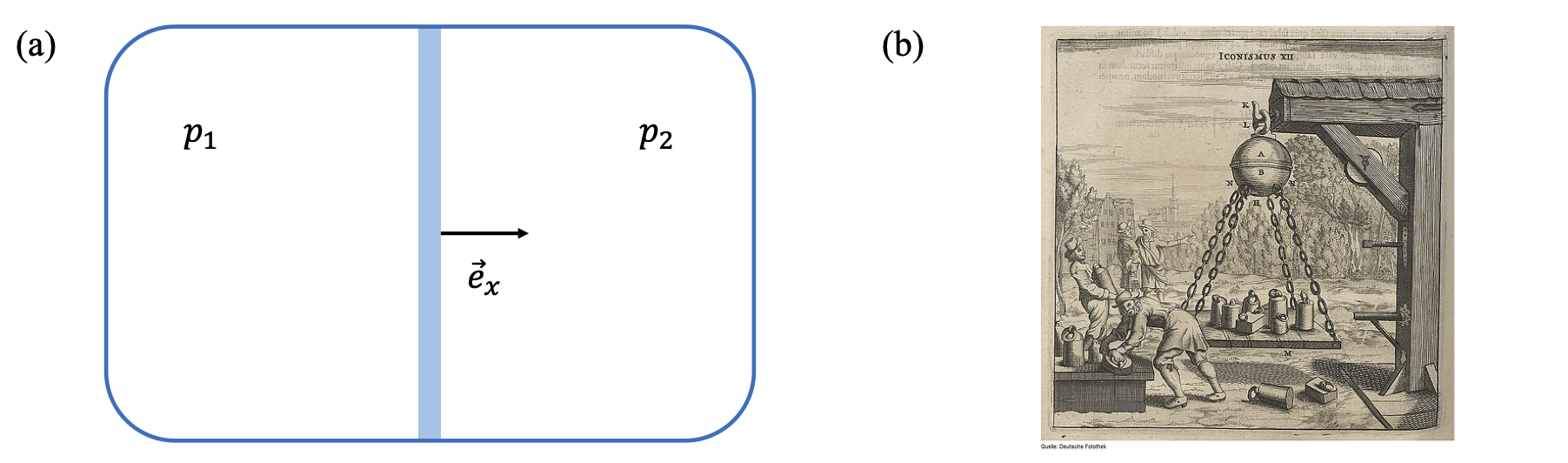
Gauche: Enceinte séparée par une paroi. Droite: Expérience des hémisphères de Magdebourg.
Il est important de noter que les forces pressantes sont généralement considérables : par exemple, l’air à la pression atmosphérique (\(p=10^5\) Pa) exerce sur l’extrémité d’un doigt (\(S=1~\text{cm}^2\)) une force \(F=10\) N, soit l’équivalent du poids exercé par une masse de 1 kg.
Application 8.2: Otto von Guericke (1602–1686) a réalisé à Magdebourg une expérience spectaculaire mettant en évidence l’effet de la pression atmosphérique. Il réalise le vide dans un système composé de deux hémisphères de rayon \(R=28\) cm, comme représenté sur la ch8_magdebourg (b). Quelle est la force qui maintient ensemble les deux hémisphères ? Calculer la masse que l’on doit suspendre pour les séparer.
Avant de résoudre le problème, il faut décrire l’action de la force de pression sur les hemisphères. Premièrement il convient de se rappeler que en tout point de la sphère, la force de pression de l’atmosphère exerce une force perpendiculaire à sa surface, comme illustré sur la ch8_magdebourg2.
La force exercée par l’atmosphère en chaque point de la sphère est perpendiculaire à la tangente.
seuls les composants normaux au plan de contact entre les deux hémisphères agissent activement pour les maintenir ensemble.
Ensuite, il convient de constater que seule les composantes normales au plan de contact vont effectivement agir, puisque du fait de la symmétrie sphérique de chacun des hémisphères les composantes parallèles vont s’annuler diamétralement, comme illustré sur la ch8_magdebourg3 ci-dessous.
Toute composante \(\vec{F}\) parallèle au plan de séparation des hémisphères, est compensée par une autre composante \(\vec{F'}\) diamétralement opposée. Seule les composantes perpendiculaires au plan de contact agissent.
Donc finalement la résultante des forces de pression est égale à la force de pression qui s’exercerait sur un disque de même rayon que les sphères: \(F=p S=p \pi r^2\). Donc:
ce qui est équivalent à un poids de 2545kg !
Équilibre hydrostatique
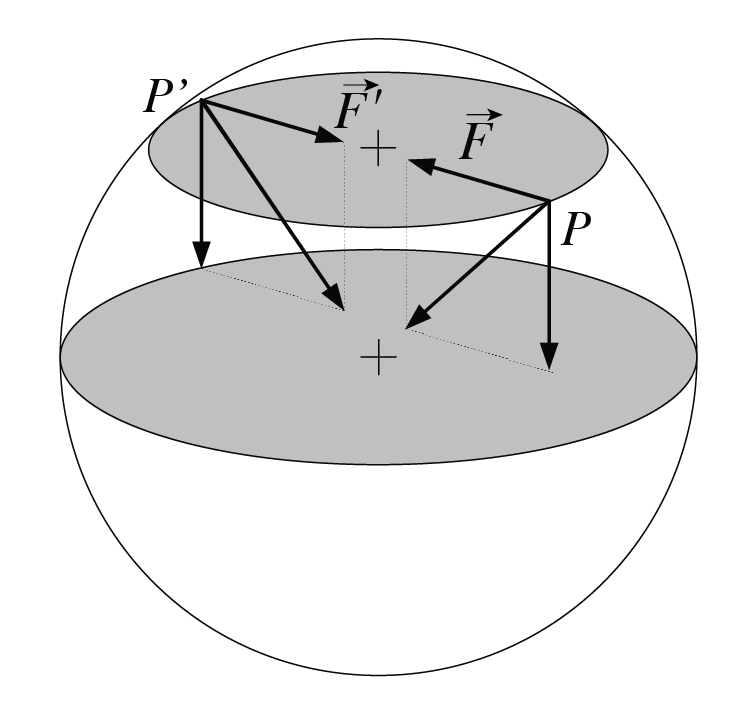
Considérons un élément de fluide de forme parallélépipédique, compris
entre les points d’abscisse \(x\) et \(x+dx\), d’ordonnée
\(y\) et \(y+dy\), et d’altitude \(z\) et \(z+dz\) —
voir le ch8_pression. Nous supposons que les
dimensions \(dx\), \(dy\) et \(dz\) sont petites comparées
aux échelles macroscopiques ; mais en même temps, elles restent grandes
par rapport aux échelles microscopiques (la taille des molécules par
exemple). On définit ainsi une particule de fluide, qui est une
particule fictive à laquelle nous pouvons appliquer les lois de la
mécanique.
Un fluide étant un milieu continu, nous allons exprimer les grandeurs physiques par unité de volume. Par exemple, la masse \(dm\) de fluide contenue dans le volume \(dV=dxdydz\) est donnée par : \(dm = \rho dV\). La particule de fluide est donc soumise à deux forces :
son poids : \(\vec{P} = dm \vec{g} = - \rho dV g \vec{e}_z\), le signe négatif provenant de l’orientation de l’axe \((Oz)\).
la résultante \(\vec{F}\) des forces de pression qui s’appliquent sur chacune des 6 faces, comme illustré sur la
ch8_pression.
La condition d’équilibre s’écrit : \(\vec{P} + \vec{F} = \vec{0}\). On projette alors cette égalité sur les trois axes.
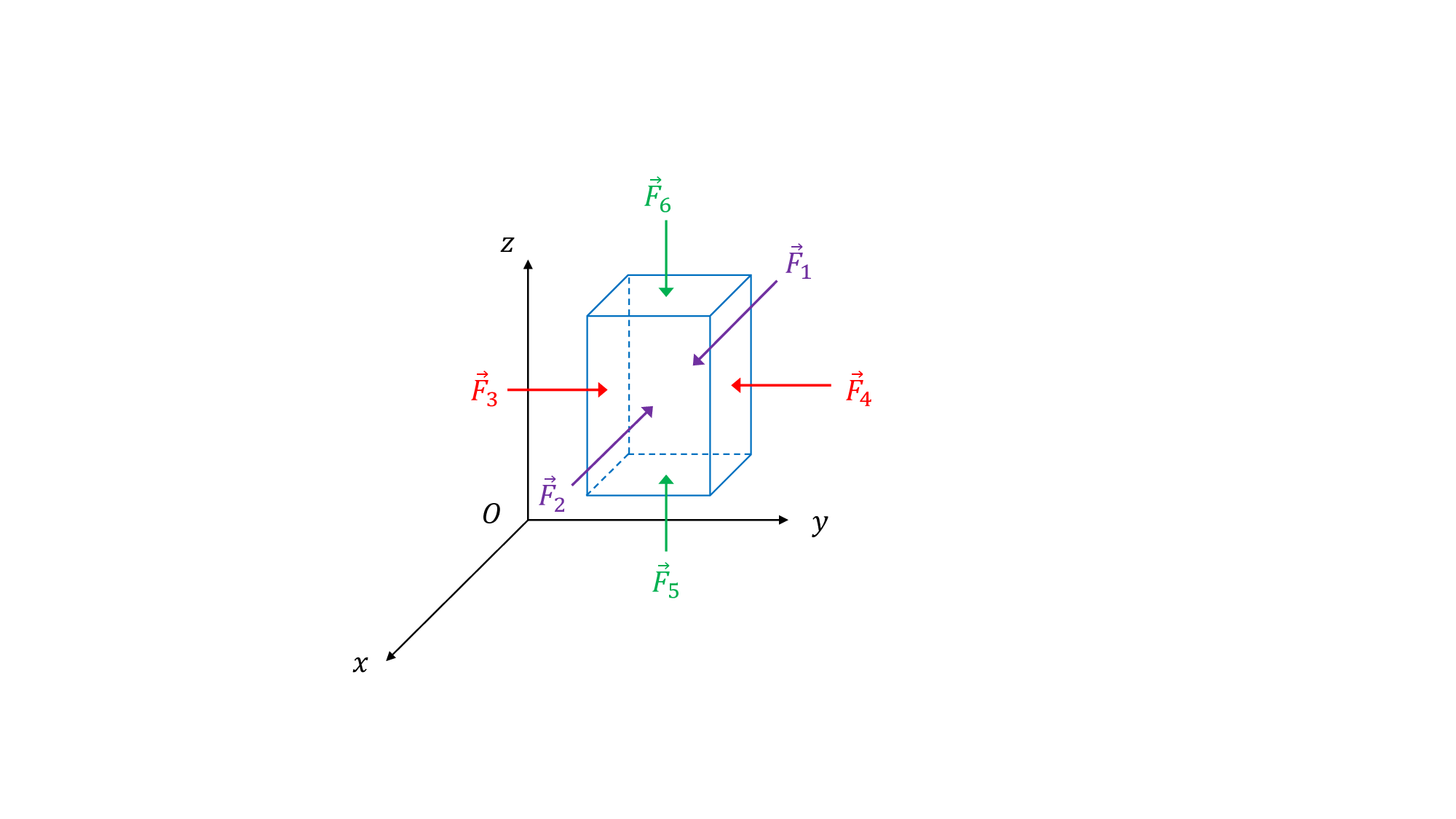
Forces de pression s’exerçant sur une particule de fluide.
Selon \((Ox)\) : l’aire des faces latérales est \(dS=dydz\). L’équilibre des forces s’écrit donc :
\[\vec{F}_1 + \vec{F}_2 = \vec{0} \quad \Rightarrow \quad p(x) dydz - p(x+dx) dy dz = 0 \quad \Rightarrow \quad \boxed{p(x+dx)=p(x) \ .}\]Autrement dit, la pression ne varie pas suivant la direction \((Ox)\).
Le même raisonnement s’applique selon \((Oy)\) :
\[\vec{F}_3 + \vec{F}_4 = \vec{0} \quad \Rightarrow \quad p(y) dxdz - p(y+dy) dx dz = 0 \quad \Rightarrow \quad \boxed{p(y+dy)=p(y) \ .}\]
Ces résultats intermédiaires nous permettent d’ores et déjà de conclure que, dans un fluide au repos, la pression est la même en tout point situé à la même altitude.
La question qui subsiste est la suivante : comment la pression varie-t-elle avec l’altitude \(z\) ? Selon \((Oz)\), l’équilibre des forces fait cette fois-ci intervenir le poids :
\[\vec{F}_5 + \vec{F}_6 + dm \vec{g} = \vec{0} \quad \Rightarrow \quad p(z) dxdy - p(z+dz) dx dy - \rho gdxdydz = 0 \ .\]
Or si \(dz\) est suffisamment petit, on peut écrire simplement que:
Après simplification, on obtient la relation fondamentale de l’hydrostatique :
Cette relation exprime l’équilibre entre la pesanteur et les forces de pression au sein du fluide. Elle implique en particulier que la pression décroît avec l’altitude.
Interface entre deux fluides
Definitions
1.1 Une interface est la frontière qui sépare deux fluides dont les propriétés physiques sont différentes, comme par exemple deux liquides immiscibles, ou un liquide et un gaz.
À l’équilibre hydrostatique, les pressions de part et d’autre d’une interface sont égales. Considérons en effet une portion d’aire \(S\) de l’interface séparant deux fluides. Chacun des fluides exerce une force pressante de norme \(f_{\pm} =p_{\pm} S\). Les deux forces sont orientées en sens opposé. Le système étant au repos, les forces se compensent : \(\text{d}\vec{f}_+ + \text{d}\vec{f}_- = \vec{0}\), ce qui implique : \(p_+=p_-\).
Application aux fluides incompressibles
Notion d’incompressibilité
Definitions
1.2 Un fluide est dit incompressible si sa masse volumique est indépendante de la pression. Mathématiquement, ceci s’exprime par l’égalité: \(\rho=\text{constante}\)
En première approximation, on pourra supposer que les liquides sont incompressibles (même s’ils présentent en réalité une faible compressibilité). C’est également le cas des gaz pour de faibles différences de hauteur.
Relation de l’hydrostatique pour un fluide incompressible
La relation de l’hydrostatique est une relation locale, en ce sens qu’elle relie la dérivée de la pression à la masse volumique \(\rho\) du liquide. Or, si le fluide est incompressible (i.e., \(\rho=\text{constante}\)), on peut intégrer la relation () pour obtenir :
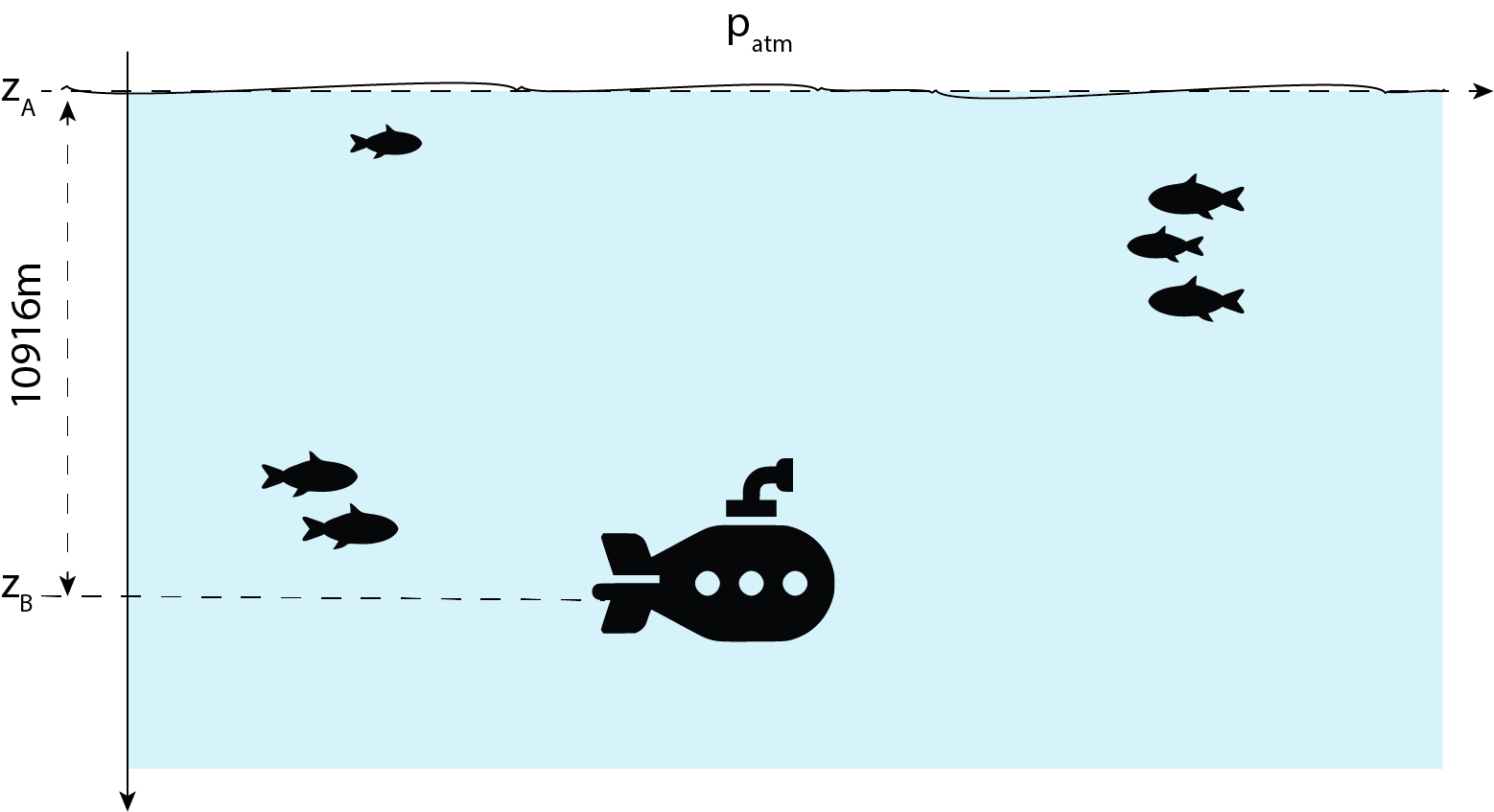
où \(C\) est une constante. Pour appliquer cette dernière relation, on considère deux points \(A\) et \(B\) situés aux altitudes \(z_A\) et \(z_B\). La différence de pression entre \(A\) et \(B\) est alors donnée par :
On pourra appliquer directement ce résultat si les hypothèses suivantes sont vérifiées :
le fluide est au repos.
le fluide est incompressible.
l’axe vertical \((Oz)\) est orienté vers le haut [2].
Afin d’illustrer la formule (), supposons par exemple que \(z_B>z_A\) et calculons la différence de pression \(\Delta p=p_A-p_B\) (on rappelle que la pression décroît avec l’altitude) entre deux points séparés de la hauteur \(h=z_B-z_A=10\) m :
dans l’eau : \(\Delta p = \rho_{\textrm{eau}}gh\approx 10^5~\text{Pa} \approx 1~\text{atm}\). La pression varie de \(1~\text{atm}\) tous les 10 m environ.
dans l’air : \(\Delta p = \rho_{\textrm{air}}gh\approx 10^2~\text{Pa} \approx 0,001~\text{atm}\). La pression ne varie que de \(0,1\%\) de la pression atmosphérique sur une hauteur de 10 m.
En pratique, tant que les différences de hauteur resteront inférieures au km, on pourra négliger les variations de pression dans l’air.
Application 8.3: En janvier 1960, l’océanographe J. Piccard atteint à bord de son bathyscaphe « Trieste » la profondeur de \(10\ 916\) m dans la fosse des Mariannes (Océan Pacifique). Calculer la pression à laquelle doit résister le bathyscaphe. On donne : \(p_{\textrm{atm}}=1,013\times 10^5\) Pa.
Schéma de l’océanographe Picard.
La relation () s’écrit ici:
avec:
On obtient donc:
Photographie du bathyscaphe Trieste inventé par Auguste Piccard, père de Jacque Piccard, qui l’utilisa pour atteindre le fond des fosses Mariannes à -10916m
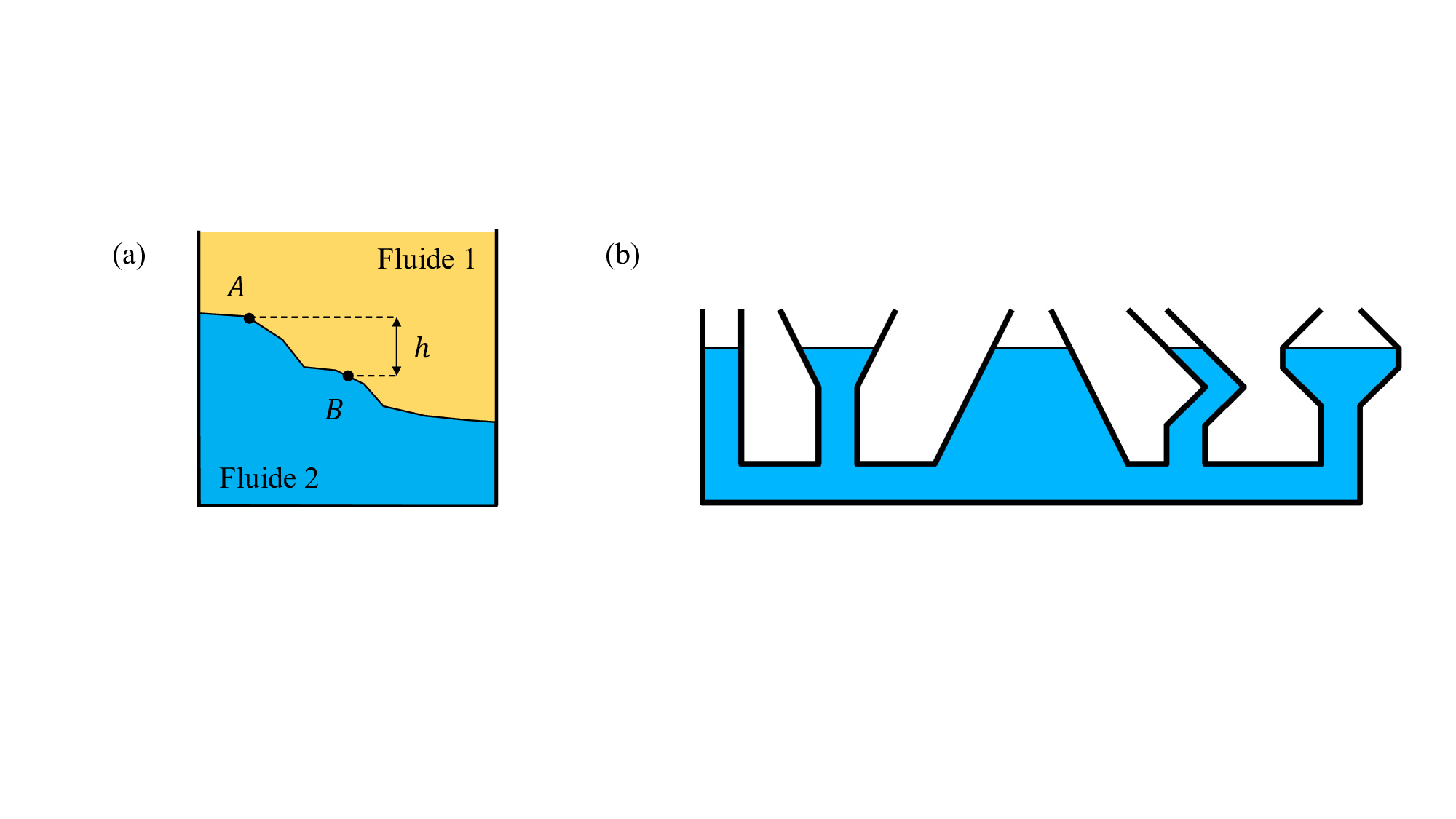
Gauche: Interface fictive entre deux fluides. Droite: Principe des vases communiquants.
Principe des vases communiquants
Un conséquence directe de la relation () est
qu’une interface entre deux fluides au repos est horizontale. Pour
justifier cette proposition, considérons la situation présentée sur la
ch8_vases (a) et exprimons la différence de pression
entre deux points \(A\) et \(B\) situés sur l’interface séparant
deux fluides non miscibles :
dans le fluide 1 : \(p_A-p_B = -\rho_1 g (z_A-z_B)\).
dans le fluide 2 : \(p_A-p_B = - \rho_2 g (z_A-z_B)\).
Ceci implique donc l’égalité : \(\rho_1 g (z_A-z_B)= \rho_2 g (z_A-z_B)\). Or les masses volumiques \(\rho_1\) et \(\rho_2\) étant différentes, on a nécessairement : \(z_A=z_B\). Autrement dit, l’interface est plane.
On peut en déduire le principe des vases communiquants : lorsqu’un
liquide remplit plusieurs récipients connectés entre eux et soumis à la
pression atmosphérique, les niveaux des interfaces s’équilibrent à une
hauteur qui est identique dans tous les récipients. Ceci est vrai quel
que soit la forme et le volume des récipients — voir la
ch8_vases (b). Si on ajoute du liquide dans l’un des
récipients, les niveaux s’équilibrent à nouveau dans l’ensemble des
récipients.
Méthodologie
Résumons les principaux résultats obtenus jusqu’ici :
dans un fluide incompressible, la différence de pression entre deux points \(A\) et \(B\) est proportionnelle à la différence de leurs altitudes : \(p_B-p_A= -\rho g (z_B-z_A)\).
la pression est continue au passage d’une interface qui sépare deux liquides immiscibles ou un liquide et un gaz. En outre, l’interface est horizontale.
Avertissement
Il est important de noter qu’on ne peut pas appliquer la relation de l’hydrostatique entre deux points situés dans des fluides différents. En effet, si les masses volumiques ne sont pas les mêmes, on doit appliquer deux fois la relation de l’hydrostatique en faisant intervenir un point intermédiaire situé sur l’interface. En pratique, on introduira autant de points intermédiaires qu’il y a d’interfaces.
Mesure de la pression atmosphérique : le baromètre de Torricelli
Afin de mesurer la pression atmosphérique, Evangelista Torricelli
(1608–1647) inventa en 1643 à Florence le baromètre à mercure. Le
mercure est un métal qui présente la particularité d’être liquide à
température ambiante. Le principe du baromètre de Torricelli est
illustré sur la ch8_torricelli: un long tube de
verre, fermé à l’une de ses extrémités, est plongé dans un bain de
mercure. Lorsqu’on le relève à la vertical, le tube ne se vide que
partiellement (tant que la partie ouverte du tube reste immergée). La
hauteur de la colonne de mercure qui subsiste à l’intérieur du tube est
\(h\approx 760\) mm. Elle est directement reliée à la pression de
l’air.
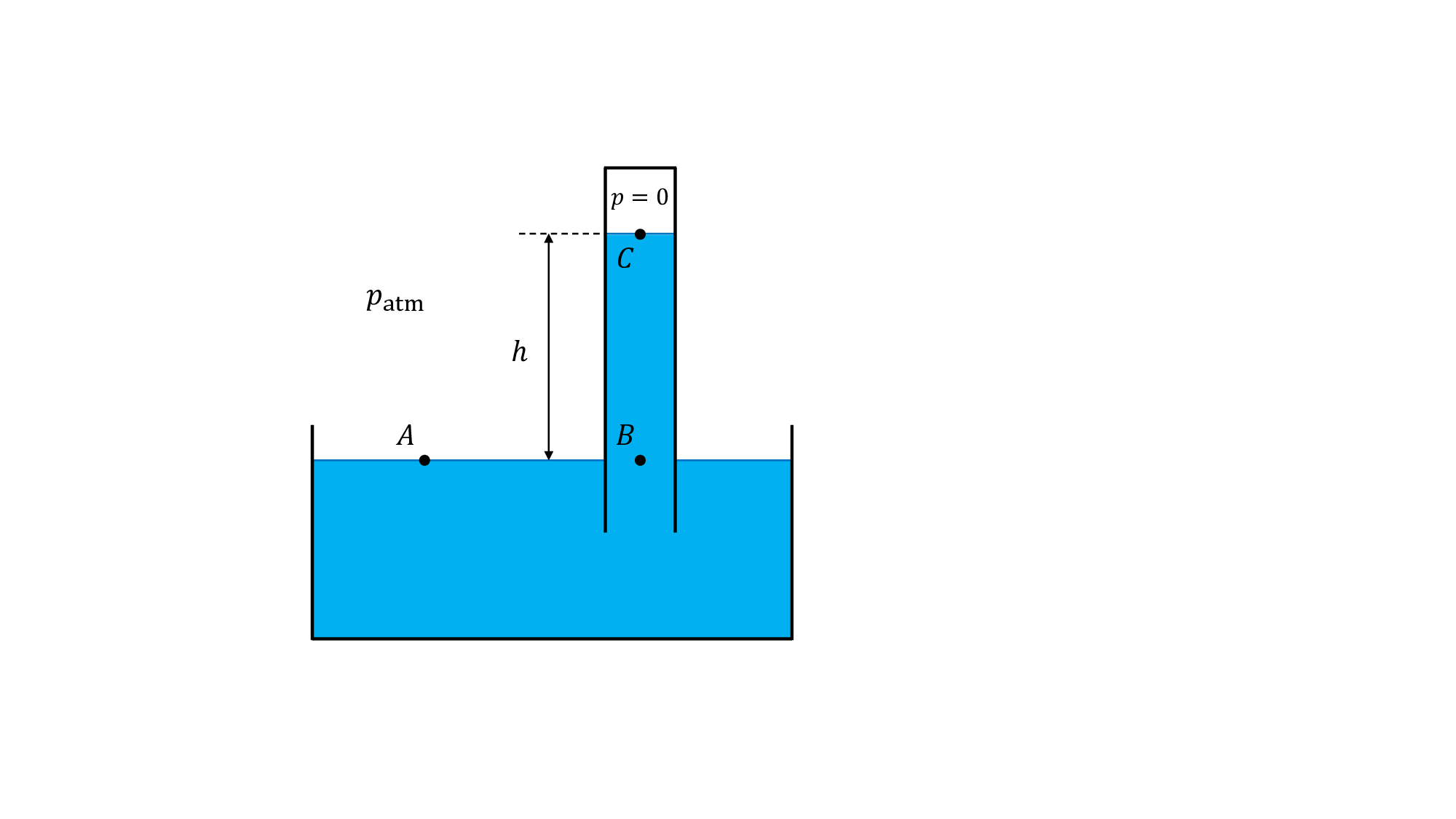
Principe du baromètre de Torricelli.
Pour comprendre le fonctionnement du baromètre de Torricelli, on définit
les points \(A\), \(B\) et \(C\) qui sont indiqués sur la
ch8_torricelli:
le point \(A\) est situé à l’interface avec l’air : sa pression est donc \(p_A=p_{\textrm{atm}}\).
les points \(A\) et \(B\) sont situés à la même altitude dans le même fluide (le mercure) : \(p_B=p_A\).
lorsque le tube est mis à la verticale, on crée le vide dans sa partie supérieure : \(p_c=0\).
enfin, on applique la relation de l’hydrostatique entre \(B\) et \(C\) : \(p_B-p_C=-\rho g(z_B-z_C)=\rho gh\).
En regroupant tous ces résultats, on obtient finalement :
Le baromètre de Torricelli sera utilisé en particulier par Blaise Pascal (1623–1662), qui démontra en 1648 à Clermont-Ferrand que la pression de l’air décroît bien avec l’altitude. L’importance de ses travaux en hydrostatique conduiront à donner son nom à l’unité de pression : le pascal (Pa). Torricelli a quant à lui laissé son nom à une autre unité, le torr (\(1~\text{Torr} = 1~\text{mmHg}\)), qui est encore couramment utilisée en physique des très basses pressions.
La poussée d’Archimède
Énoncé historique
Dans son « Traité des corps flottants », Archimède (287 av. J.-C.–212 av. J.-C.) étudie la flottabilité des corps dans un liquide. Il y formule son célèbre principe :
Loi
1.3 (Principe d’Archimède). Tout corps plongé dans un fluide au repos, en immersion totale ou partielle, subit de la part de ce fluide une force verticale ascendante, dont l’intensité est égale au poids du volume de fluide déplacé.
Il fallut attendre le XVII\(^{\text{e}}\) siècle et les progrès de l’hydrostatique pour démontrer ce résultat.
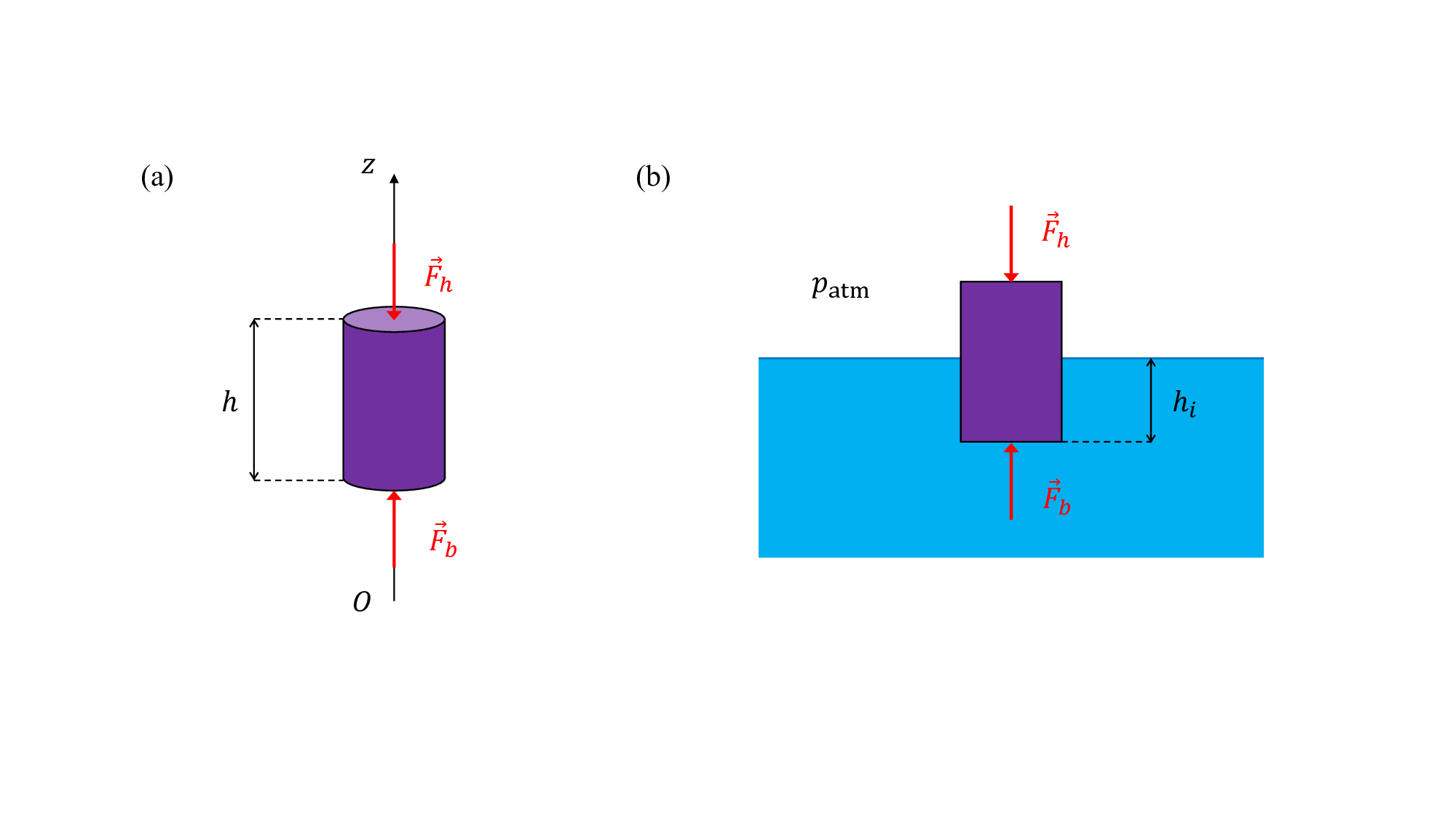
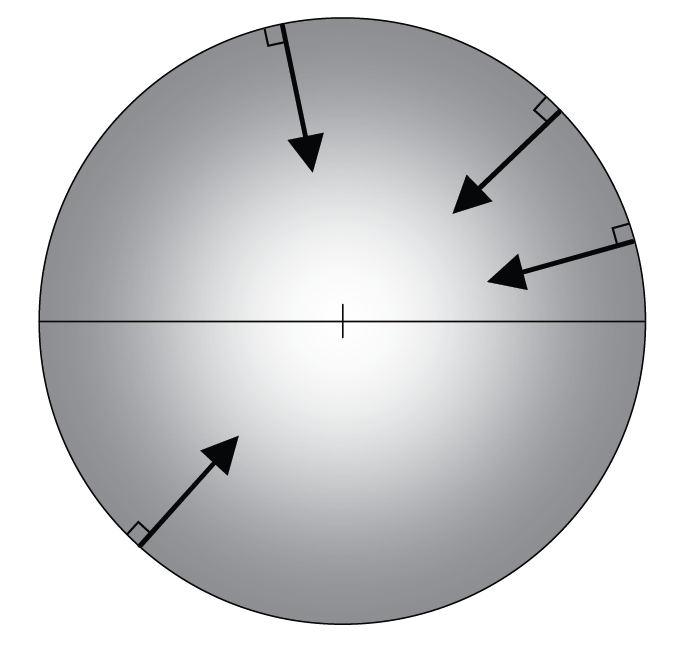
La poussée d’Archimède est la résultante des forces de pressions qui s’exercent sur un corps (a) totalement ou (b) partiellement immergé dans un fluide.
Résultante des forces de pression
La poussée d’Archimède découle de la variation de la pression avec l’altitude : la pression étant plus forte sur la partie inférieure d’un corps immergé que sur sa partie supérieure, la résultante des forces est verticale ascendante. Nous allons discuter séparément les deux configurations qui peuvent se présenter : soit le corps est totalement immergé dans le fluide, soit il flotte à l’interface avec l’air.
Corps entièrement immergé
Considérons un corps solide plongé dans un fluide de masse volumique
\(\rho\). Pour simplifier la discussion [3], on supposera que le
solide est un cylindre de hauteur \(h\) et de volume
\(V = S \times h\), voir la ch8_archimede (a). On
effectue alors le bilan des forces exercées par le fluide sur les
différentes faces du cylindre :
à profondeur fixée, les forces qui s’exercent de part et d’autre de la surface latérale se compensent. La composante horizontale de la résultante des forces de pression est donc nulle par symétrie.
notons \(p_h\) et \(p_b\) les pressions qui s’exercent sur chacune des faces horizontales (les indices \(h\) et \(b\) correspondant à « haut » et « bas ») . Si \(\vec{e}_z\) est le vecteur unitaire de l’axe vertical ascendant, la résultante des forces de pression s’écrit :
\[\vec{\pi} = \vec{F}_b+ \vec{F}_h=\left(p_b - p_h \right) S\, \vec{e}_z \ .\]
Il ne reste plus qu’à exprimer la différence de pression à l’aide de la relation fondamentale de l’hydrostatique : \(p_b-p_h = \rho g h\), ce qui donne finalement :
Corps partiellement immergé
Reprenons le raisonnement dans le cas d’un corps flottant à l’interface
avec l’air, comme représenté sur la ch8_archimede. On
néglige la variation de pression avec l’altitude dans l’air. On note
\(h_{i}\) la hauteur immergée du cylindre. Comme précédemment, seule
la composante verticale de la résultante des forces de pression est non
nulle :
sur la face supérieure, la pression est \(p_{\textrm{atm}}\) et donc \(\vec{F}_h=-p_{\textrm{atm}}S \, \vec{e}_z\).
sur la face inférieure, on a : \(\vec{F}_b=p_bS \, \vec{e}_z\).
la différence de pression entre la surface inférieure et l’interface est donnée par la relation de l’hydrostatique : \(p_b-p_{\textrm{atm}}=\rho g h_{i}\). La résultante \(\vec{\pi} = \vec{F}_b+ \vec{F}_h\) est donc :
\[\vec{\pi}= \rho V_{i}g \vec{e}_z \ ,\]où \(V_{i}=Sh_{i}\) est le volume immergé du corps solide.
Formulation générale
Nous pouvons maintenant récapituler ces résultats en une formulation unique : la poussée d’Archimède \(\vec{\pi}\) est la résultante des forces de pression qui s’exercent sur un corps en immersion totale ou partielle. Mathématiquement, cette force est donnée par :
où \(V_{i}\) est le volume immergé, et \(\vec{g}=-g\vec{e}_z\). On voit donc que la poussée d’Archimède est égale à l’opposé du poids \(\vec{P} = m \vec{g}\) (avec \(m=\rho V_{i}\)) du volume de fluide déplacé par le corps solide.