7. Thermodynamique
La thermodynamique est la science qui étudie les phénomènes thermiques, en relation avec les autres domaines de la physique (mécanique, électromagnétisme, …). Son développement est intimement lié à la Révolution industrielle qui a bouleversé l’économie aux XVIII\(^{\text{e}}\) et XIX\(^{\text{e}}\) siècles. Dans ce chapitre, nous présentons d’abord les différents états de la matière. Nous introduisons ensuite les notions fondamentales de température et de pression, que nous appliquons au modèle du gaz parfait.
Les états de la matière
La matière qui nous entoure est constituée d’atomes, d’ions et de molécules — nous utiliserons par la suite le terme générique de particules — qui s’organisent dans l’espace pour former différentes phases. Dans le cas d’un corps pur, c’est-à-dire une substance qui ne contient qu’un seul type d’élément chimique, les trois états les plus courants sont l’état solide, l’état liquide et l’état gazeux.
L’état solide est un état dense de la matière. Un solide possède une forme propre et est difficilement compressible. Dans un solide, l’énergie potentielle d’interaction des particules est grande devant l’énergie cinétique.
L’état liquide est également un état dense de la matière. Un liquide s’adapte à la forme de son récipient mais reste peu compressible. Ses constituants peuvent se mouvoir les uns par rapport aux autres. Dans un liquide, l’énergie cinétique est comparable à l’énergie d’interaction.
L’état gazeux est quant à lui un état dilué de la matière. Un gaz est facilement compressible. Il n’a pas de forme ni de volume propre, mais tend à occuper tout le volume qui lui est accessible. Ses constituants interagissent très peu, leur énergie cinétique est grande devant l’énergie potentielle d’interaction.
Les liquides et les gaz possèdent tous deux la propriété de s’écouler : ces sont des fluides. Dans un solide ou dans un liquide, la distance typique \(d\) séparant deux particules est comparable à la taille \(a\) des constituants : \(d \sim a \sim 1~\text{Å}\). Ceci n’est pas le cas dans un gaz où l’on a : \(a \sim 1~\text{Å} \ll d\).
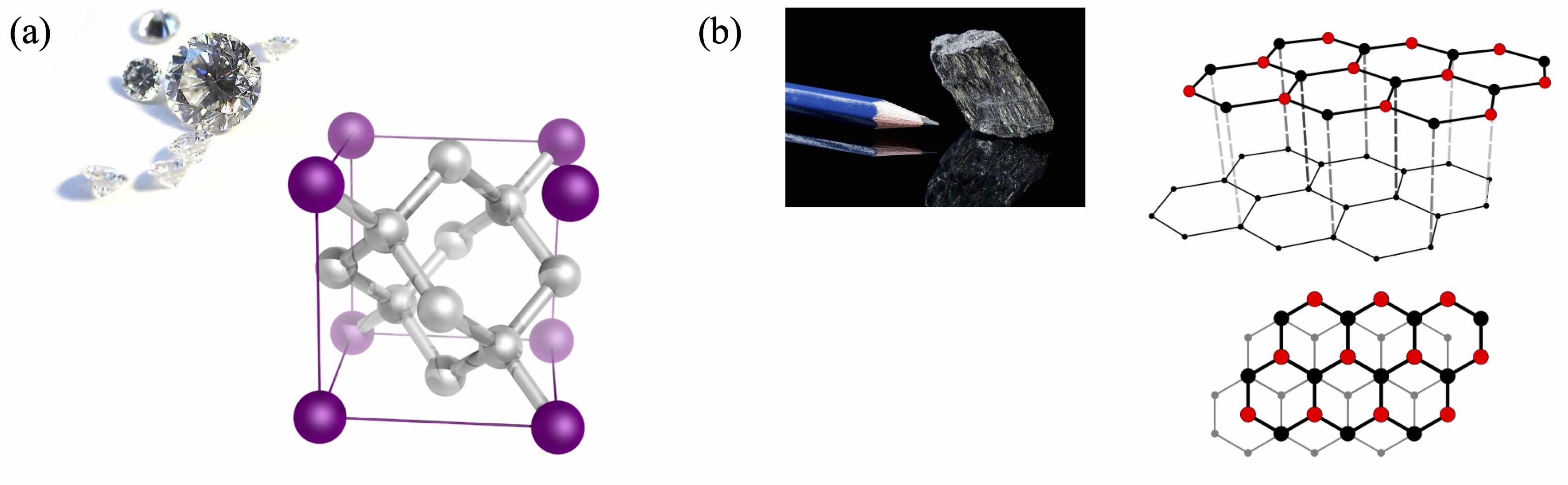
Structure cristalline de deux allotropes du carbone : (a) diamant et (b) graphite.
En pratique, la situation est plus complexe que ne laisse penser cette
classification rudimentaire. En effet, un composé à l’état solide peut
présenter plusieurs formes avec des propriétés physiques très
différentes : on parle de formes allotropiques. C’est par exemple le
cas du carbone : cet élément se retrouve sous la forme commune de
graphite, mais aussi sous la forme plus rare de diamant. Elles se
différencient par leur structure cristalline, c’est-à-dire
l’arrangement des atomes au niveau microscopique, comme illustré sur la
ch7_structures.
Les états de la matières sont donc caractérisés de façon plus rigoureuse par l’organisation microscopique de leurs constituants. On trouve également des matériaux qui combinent à la fois les propriétés d’un liquide ordinaire et celles d’un solide cristallisé. Ce sont les cristaux liquides, dont les propriétés physiques singulières ont des applications dans de nombreux domaines technologiques (écrans LCD par exemple). Il existe en réalité toute une variété d’états plus « exotiques » de la matière, que nous ne discuterons pas ici.
Enfin, il est important de mentionner que l’état de la matière le plus commun n’est ni solide, ni liquide, ni gazeux. En effet, la forme la plus abondante dans l’univers est l’état plasma : il s’agit d’un gaz ionisé de particules chargées (ions et électrons), qui constitue plus de 99 % de la matière connue actuellement dans l’univers (étoiles, nébuleuses, vents solaires, …).
Les variables thermodynamiques
Un échantillon macroscopique de matière est composé d’un nombre astronomiquement grand de particules, dont l’ordre de grandeur est donné par le nombre d’Avogadro \(\mathcal{N}_A\). Le nombre d’Avogadro est une constante fondamentale dont la valeur a été fixée par convention :
Ce nombre est tellement grand qu’il est impossible, même avec les ordinateurs actuels, de résoudre les équations du mouvement d’un système macroscopique composé de \(\mathcal{N}_A\) particules. Le point de vue de la thermodynamique consiste alors à réduire le nombre de variables pour ne retenir que quelques grandeurs physiques, que nous allons maintenant définir.
Volume
La variable la plus évidente est le volume, qui caractérise l’extension spatiale du système étudié. L’unité SI de volume est le \(\text{m}^3\). Une unité dérivée commune est le litre : \(1~\ell=1~\text{dm}^3=10^{-3}~\text{m}^3\).
Quantité de matière
Dans un système macroscopique, le nombre \(N\) de particules est généralement très grand. Il s’avère plus commode de mesurer la quantité de matière en moles. Le nombre de moles \(n\) est défini par :
On définit également la masse molaire \(M=m/n\), où \(m\) est la masse de la substance étudié. Dans le système international, la masse molaire s’exprime en \(\text{kg} \cdot \text{mol}^{-1}\), mais on utilise plus couramment le \(\text{g} \cdot \text{mol}^{-1}\). Enfin, à partir de la masse et du volume, on construit la masse volumique \(\rho = m/V\) (unité SI : \(\text{kg}\cdot\text{m}^{-3}\)).
Pression
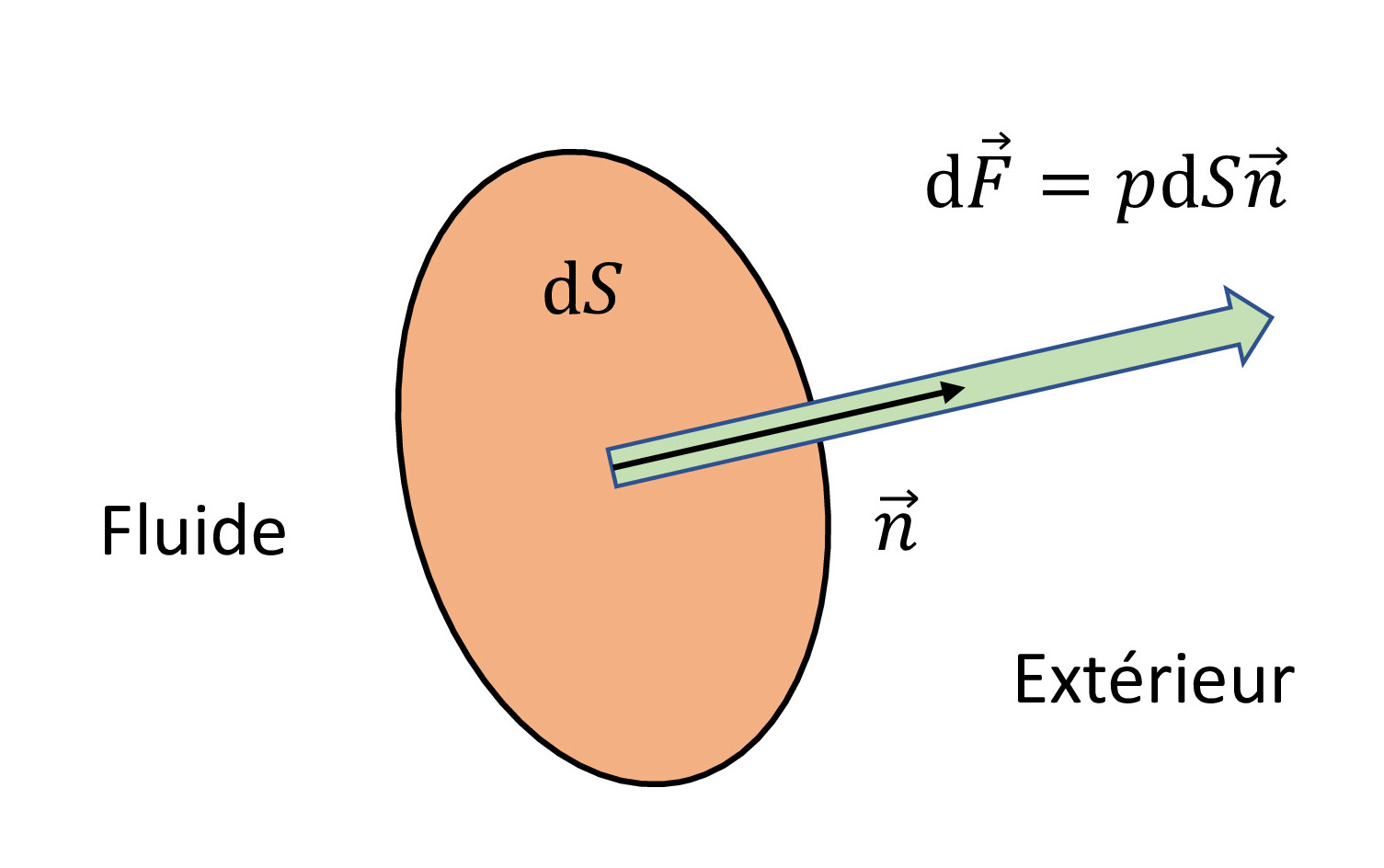
Pour caractériser l’intensité de la force exercée par un fluide sur une
surface, on introduit la notion de pression. Considérons la surface
infinitésimale \(\text{d}S\) représentée sur la ch7_pressure. La résultante
\(\text{d}\vec{F}\) des forces appliquées par le fluide
perpendiculairement à cet élément de surface est définie par :
où \(\vec{n}\) est le vecteur unitaire (\(\Vert \vec{n} \Vert = 1\)) normal à la surface.
La pression est donc définie comme la force par unité de surface qui s’exerce perpendiculairement à cette surface. La force de pression est toujours dirigée vers l’extérieur (du fluide vers la surface). Il s’agit d’une quantité isotrope, donc indépendante de l’orientation de la surface. L’unité SI de pression est le pascal : \(1~\text{Pa} = 1~\text{N} \cdot \text{m}^{-2}= 1~\text{kg}\cdot \text{m}^{-1} \cdot \text{s}^{-2}\). On utilise également le bar : \(1~\text{bar} = 10^{5}~\text{Pa}\), ainsi que l’atmosphère : \(1~\text{atm}=1,01325 \times 10^{5}~\text{Pa}\). Notons que, si la pression est constante sur une surface macroscopique d’aire \(S\), alors la norme \(F\) de la force de pression est donnée par :

L’astronaute américaine Tracy Caldwell dans la coupole d’observation de l’ISS.
Température
La température \(T\) est la grandeur physique caractérisant l’état thermique d’un système. L’unité SI de température est le kelvin (K). Bien que la notion de température nous soit familière, sa définition scientifique rigoureuse est complexe. Nous verrons ci-dessous que la température est liée à l’agitation thermique, c’est-à-dire le mouvement aléatoire et incessant des atomes et molécules qui composent la matière.
Dans la vie quotidienne, le kelvin n’est pas l’unité la plus pratique. L’échelle de température usuelle est l’échelle Celsius, dont l’unité est le degré (symbole : \(^{\circ}\)C). Historiquement, cette échelle a été construite à partir de deux phénomènes physiques : le point de solidification de l’eau, qui définit la température de \(0^{\circ}\)C, et le point de vaporisation de l’eau, qui définit la température de \(100^{\circ}\)C. Les échelles Kelvin et Celsius sont simplement décalées l’une par rapport à l’autre :
Il existe également d’autres échelles de température, dont l’échelle Fahrenheit (symbole : \(^{\circ}\text{F}\)) qui est encore très répandue en Amérique du Nord. Cette dernière est homothétique à l’échelle Celsius. La règle de conversion est donnée par la formule suivante :
Abordons pour finir l’évolution vers l’équilibre d’un système composé de deux corps \(\mathcal{C}_1\) et \(\mathcal{C}_2\), dont les températures initiales \(T_1\) et \(T_2\) sont différentes (\(T_1<T_2\) par exemple). Lorsqu’on les met en contact, les transferts d’énergie thermique vont toujours du corps le plus chaud vers le corps le plus froid. Le processus se poursuit jusqu’à ce que les températures s’équilibrent à une valeur commune \(T_f\) qui est telle que : \(T_1 \leq T_f \leq T_2\).
Le modèle du gaz parfait
Afin d’illustrer de façon concrète les notions de température et de pression, nous discutons maintenant les propriétés du gaz parfait. Historiquement, l’équation d’état des gaz parfaits résulte de nombreuses lois empiriques établies au cours de plus de deux siècles d’observations expérimentales.
Loi de Boyle-Mariotte
À la fin du XVII\(^{\text{e}}\) siècle, Boyle (1627-1691) et Mariotte (1620-1695) observent que, lors d’une transformation isotherme (à température constante), le produit de la pression et du volume occupé par le gaz est constant :
La valeur de la « constante » dépend de la température, mais elle n’a pas nécessairement besoin d’être connue. En effet, si l’on note \(p_1\) et \(V_1\) (respectivement \(p_2\) et \(V_2\)) la pression et le volume au début (resp. à la fin) d’une transformation entre deux états 1 et 2, alors on a l’égalité :
Loi de Charles
Près d’un siècle plus tard, le physicien français Charles (1746-1823) étudie expérimentalement la dilatation des gaz. Il montre que, lors d’une transformation isobare (à pression constante) entre deux états 1 et 2, le rapport du volume d’un gaz et de sa température absolue est constant :
Loi de Gay-Lussac
Dans la continuité des travaux de Charles, Gay-Lussac (1778-1850) démontre que, lors d’une transformation isochore (à volume constant) entre deux états 1 et 2, le rapport de la pression d’un gaz et de sa température absolue est lui aussi constant :
Loi d’Avogadro
En combinant les trois lois que nous venons d’évoquer, nous pouvons conclure que la pression, le volume et la température d’un gaz vérifient la relation :
où \(K\) est une constante. Cependant, pour obtenir l’équation des gaz parfaits sous sa forme la plus générale, il faut tenir compte d’un paramètre supplémentaire : la quantité de matière. C’est le physicien italien Avogadro (1776-1856) qui établit que, à pression et température données, tous les gaz occupent le même volume molaire :
Notons que cette loi n’a pas le même statut que les précédentes : en effet, elle repose sur une hypothèse — purement spéculative à l’époque — selon laquelle la matière est constituée d’atomes et de molécules. Il faudra attendre le tournant du XX\(^{\text{e}}\) siècle pour que cette description soit établie définitivement (avec en particulier la mesure du nombre d’Avogadro par Jean Perrin en 1908).
Loi des gaz parfaits
En regroupant tous les résultats précédents, nous pouvons déduire que la constante \(K\) dans l’équation () doit être proportionnelle au nombre de moles \(n\). Ce travail de synthèse a été effectué par Émile Clapeyron (1799-1864), qui énonce en 1834 l’équation d’état du gaz parfait :
Cette formule fait intervenir une constante, \(R\), appelée constante des gaz parfaits :
Cette constante est universelle, c’est-à-dire que sa valeur est indépendante de l’espèce chimique considérée.
Éléments de théorie cinétique des gaz
Il a fallut attendre l’avènement de la physique statistique, développée à partir de la seconde moitié du XIX\(^{\text{e}}\) siècle, pour fournir une interprétation microscopique à la loi phénoménologique des gaz parfait. Pour ce faire, nous adoptons une description probabiliste de l’agitation thermique.
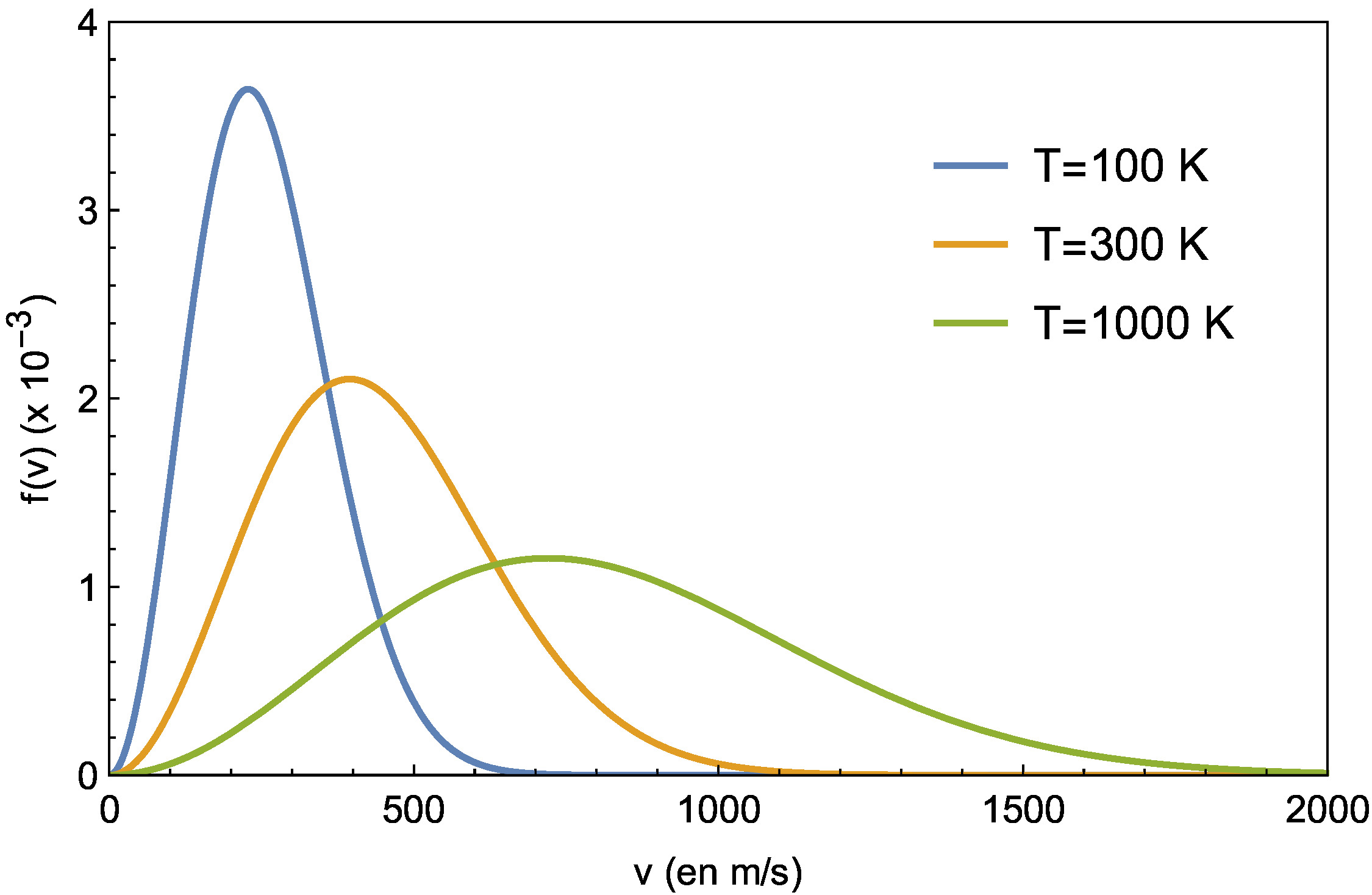
Loi de distribution des vitesses du dioxygène pour différentes valeurs de la température.
Distribution des vitesses
Au niveau microscopique, le mouvement des molécules apparaît complètement désordonné. En suivant un raisonnement basé sur les probabilités, le physicien écossais J.C. Maxwell (1831-1879) démontre en 1860 que la distribution de probabilité des vitesses \(f(v)\) est donnée par :
où \(k_B\) est la constante de Boltzmann :
La fonction \(f(v)\) est représentée sur la
ch7_mb. On remarque en particulier que la courbe passe
par un maximum qui correspond à la vitesse \(v_p\) la plus probable
:
Connaissant la densité de probabilité, il est possible de calculer les valeurs moyennes des quantités impliquant la vitesse. On obtient ainsi le théorème d’équipartition de l’énergie :
Ce résultat illustre le lien entre la notion macroscopique de température et l’énergie cinétique des molécules. On définit encore la vitesse thermique des molécules :
On utilisera cette définition pour caractériser l’agitation thermique des molécules d’un gaz.
La formule () a une conséquence importante. L’énergie cinétique étant toujours positive, il en est de même pour la température thermodynamique. La température \(T=0~\text{K}=-273,15^{\circ}\text{C}\) représente donc le minimum absolu de température. Cette température théorique correspond à une absence de mouvement, c’est-à-dire une situation où toutes les particules seraient figées. En réalité, cette image n’est pas strictement valide car la physique à très basse température est dominée par la mécanique quantique. Les effets quantiques confèrent à la matière des propriétés singulières (supraconductivité, superfluidité, …) lorsqu’on s’approche du zéro absolu. À ce jour, la température la plus basse qui ait été atteinte expérimentalement est de l’ordre du nanokelvin (\(1~\text{nK}=10^{-9}\) K).
Pression cinétique
Partant du mouvement aléatoire des molécules d’un gaz au niveau microscopique, nous allons maintenant calculer la pression exercée par le gaz. Nous supposons que le gaz est composé de \(N\) particules ponctuelles dans un récipient cubique de volume \(V=L^3\). Nous faisons l’hypothèse que la distribution des particules est uniforme et que les vitesses suivent la loi de probabilité (). En outre, seuls les chocs — entre particules ou avec les parois — ont une influence, les autres interactions étant négligeables.
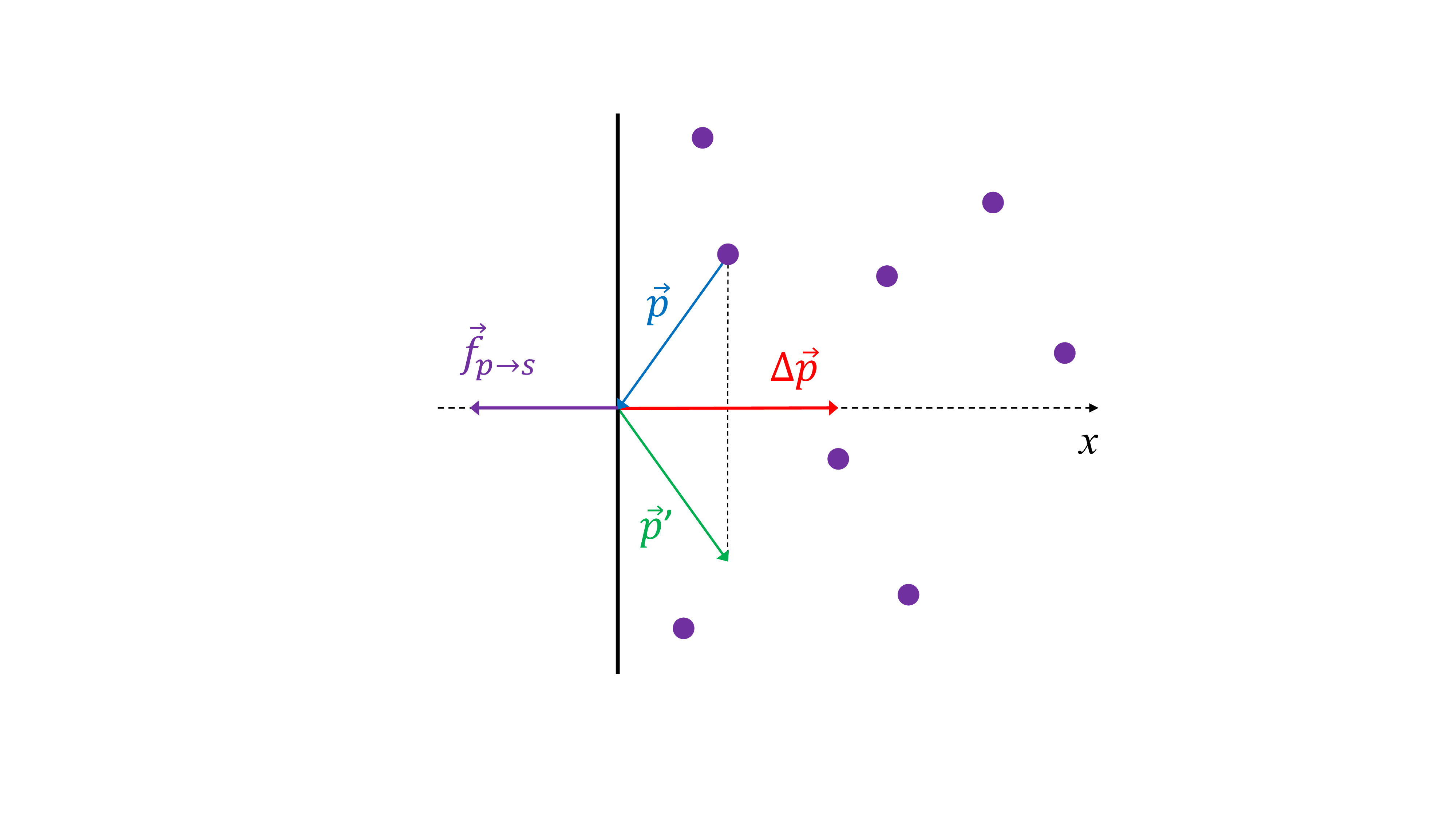
Considérons tout d’abord le choc d’une particule sur l’une paroi : comme représenté sur le schéma ci-dessus, la paroi est choisie perpendiculaire à l’axe \((Ox)\). Dans ce référentiel, les vitesses avant et après le choc s’écrivent (en notant avec un prime les grandeurs physiques après le choc):
On suppose que le choc est élastique, c’est-à-dire que la norme de la quantité de mouvement \(\vec{p}=m\vec{v}\) est conservée. Les composantes de la vitesse en \(y\) et \(z\) sont inchangées en norme et en direction, tandis que la composante en \(x\) après le choc aura la même norme mais sera de direction opposée, et nous pouvons donc écrire :
Les impulsions s’écrivent donc:
et le transfert d’impulsion \(\Delta \vec{p} = \vec{p}'-\vec{p} = m (\vec{v}'- \vec{v}) = m \Delta \vec{v} = 2mv_x\vec{e}_x\) est donc perpendiculaire à la paroi.
Cette variation d’impulsion se produit au cours d’un temps \(\Delta t\) associée à la collision. Que vaut \(\Delta t\)? La seule échelle de temps dans le problème est celle qui sépare deux chocs successifs, et qui est égale au temps que met la particule pour faire un aller-retour entre deux parois opposées: \(\Delta t = 2 L/v_x\)
Or d’après le principe fondamental de la dynamique, on a:
c’est à dire qu’on peut associer à une variation d’impulsion une force \(\vec{f}_{s\to p} = f \vec{e}_x\) exercée par la surface sur la particule, dont l’intensité est donnée par :
Pour déterminer la pression, nous avons besoin de connaître la force \(\vec{f}_{p \to s}\) exercée par la particule sur la surface. Or d’après le principe des actions réciproques, on a simplement \(\vec{f}_{p \to s}= - \vec{f}_{s\to p}\). La force de pression est donc bien orientée vers l’extérieur. La résultante des forces exercées par les \(N\) particules sur la paroi vaut alors, en moyenne :
de telle sorte que la pression, c’est-à-dire la force par unité de surface, est donnée par :
Ce résultat est important car il relie la pression, qui est une quantité macroscopique, à l’agitation thermique des particules. Or la vitesse quadratique moyenne est donnée par la distribution de Maxwell-Boltzmann. Les trois directions de l’espace étant équivalentes, on peut écrire :
En remplaçant dans l’équation () et en réarrangeant les différents termes, on démontre ainsi l’équation d’état des gaz parfaits :
Cette forme diffère de l’équation (). Or si l’on compare les deux expressions, on obtient finalement une relation entre \(R\) et les deux constantes fondamentales :