8. Statique des fluides

1. Masse de l’atmosphère terrestre \((\ast)\)

La pression atmosphérique moyenne à la surface de la Terre est : \(p_{\textrm{atm}}=1~\text{atm} = 1,013 \times 10^5~\text{Pa}\).

1. Calculer la force de pression exercée par l’air sur une surface horizontale de \(1~\text{m}^2\). En identifiant cette force avec le poids de la colonne d’air, déduire la masse correspondante.

2. Étant donné le rayon de la Terre \(R_T\approx 6400\) km, estimer la masse totale de l’atmosphère.

Solution

1. Calculer la force de pression exercée par l’air sur une surface horizontale de \(1~\text{m}^2\). En identifiant cette force avec le poids de la colonne d’air, déduire la masse correspondante.

Par définition de la pression (équation ()) on a:

\[F=p S=1.013\times10^5 \times 1= 1.013\times10^5 \text{N}\]

Cette force de pression est dûe au poids de la colonne d’air correspondante. On a donc:

\[\begin{split}\vec{F} &=\vec{P}=m\vec{g}\\ \Leftrightarrow m&=\frac{F}{g}=\frac{1.013\times10^5}{9.8}\approx10337~\text{kg}\end{split}\]

2. Étant donné le rayon de la Terre, estimer la masse totale de l’atmosphère.

La surface totale de la Terre est égale à \(4\pi R^2\approx5.05\times10^{14}\text{m}^2\).

La masse de l’atmosphère est donc égale à:

\[m=5.05\times10^{14} \times 10337 \approx 5.2\times10^{18}~\text{kg}\]

2. Tonneau de Pascal \((\ast)\)

On attribue à Pascal l’expérience présentée sur la ch8_exospression (a) : un tube de section \(s=5~\text{cm}^2\) et de longueur \(L=10\) m est relié à un tonneau rempli d’eau. On verse alors de l’eau dans le tube. La légende voudrait que le tonneau explose sous la pression de l’eau.

1. Calculer la masse d’eau contenue dans le tube.

2. Déterminer la surpression \(\Delta p = p-p_{\textrm{atm}}\) à la jonction entre le tube et le tonneau. Cette surpression dépend-elle de la section du tube ?

3. La surface interne du tonneau est \(S=2~\text{m}^2\). En supposant que la surpression est constante dans tout le tonneau, donner la force totale due à cette surpression. Comparer au poids de la colonne d’eau.

Gauche: Expérience du tonneau de Pascal. Droite: Tube en U.

Solution

1. Calculer la masse d’eau contenue dans le tube.

La masse d’eau est égale au produit du volume d’eau (\(=s \times L\)) par la masse volumique de l’eau:

\[m=\rho V = \rho s L = 1000 \times (5\times 10^{-4} ) \times 10 = 5~\text{kg}\]

2. Déterminer la surpression \(\Delta p = p-p_{\textrm{atm}}\) à la jonction entre le tube et le tonneau. Cette surpression dépend-elle de la section du tube ?

En haut du tuyau, à l’air libre, la pression est égale la pression atmosphérique \(p_0=p_{\textrm{atm}}\). D’après la relation de l’hydrostatique (équation ()), la différence de pression entre le haut et le bas du tuyau vaut:

\[\begin{split}\Delta p &=\rho g L \\ \Delta p &= 1000 \times 9.8 \times 10 = 98000~\text{Pa}\end{split}\]

On voit dans cette expression que la surpression ne dépend pas de la section du tube, mais seulement de la hauteur. Donc tout se passe comme s’il y avait une colonne complète d’eau de la même section que le tonneau et de hauteur L dans le tube.

3. La surface interne du tonneau est \(S=2~\text{m}^2\). En supposant que la surpression est constante dans tout le tonneau, donner la force totale due à cette surpression. Comparer au poids de la colonne d’eau.

La pression qu’exerce l’eau sur la face supérieure du tonneau est:

\[\begin{split}F&=\Delta p S\\ &=98000 \times 2 = 196000 \text{N}\end{split}\]

En négligeant un terme \(\rho g z\) dans le tonneau, cette force de pression est la même sur toutes les faces du tonneau. La masse équivalente à cette force serait égale à \(m_{\rm éq}=\frac{196000}{9.8}=20000\text{kg}\), alors que la masse d’eau effictivement présente dans le tube est de seulement 5kg!

On a ainsi une situation qui semble paradoxale : on exerce une force équivalente à une masse de 20 tonnes simplement en plaçant une colonne d’eau de 10m de hauteur, quelle que soit la section (et donc la masse) de cette colonne. Si la section du tuyau est de \(0.1\text{cm}^2\), alors cette colonne d’eau pèse 100g seulement, mais la force équivalente est toujours de 20 tonnes.

Cette expérience souligne le comportement très particulier de la pression dans un fluide : celle-ci est isotrope, c’est à dire identique dans toutes les directions, et le fluide « pousse » dans toutes les directions avec la même force surfacique. Remplaçons le liquide du tonneau par un solide (de la glace par exemple): la force est alors répercutée vers le bas dans la glace, et rien ne s’exerce sur la surface du tonneau.

Pour aller plus loin: la presse hydraulique

C’est sur ce principe que fonctionnent les presses hydrauliques: un circuit hydraulique ingénieusement construit permet d’appliquer des pressions considérables pour déformer ou écraser des matériaux très durs ou déplacer des objets très lourds.

3. Tube en U \((\ast \ast)\)

Un tube en U, de section \(S=1~\text{cm}^2\), contient initialement de l’eau (\(\rho_e=1000~\text{kg}\cdot \text{m}^{-3}\)). On verse dans la branche de droite un volume \(V_1=10~\text{cm}^3\) d’huile (\(\rho_h=900~\text{kg}\cdot \text{m}^{-3}\)), comme représenté sur la ch8_exospression (b).

1. Déterminer la hauteur d’huile \(h_1\).

2. En appliquant la relation fondamentale de l’hydrostatique, exprimer la différence de niveau \(\Delta h\) entre les deux surfaces libres, en fonction de \(\rho_e\), \(\rho_h\) et \(h_1\).

3. On ajoute ensuite \(V_2=20~\text{cm}^3\) de la même huile dans la branche de gauche. On note \(h_2\) la hauteur d’huile correspondante. Déterminer la nouvelle différence de niveau \(\Delta h'\) en fonction de \(\rho_e\), \(\rho_h\), \(h_1\) et \(h_2\).

Solution

1.Déterminer la hauteur d’huile \(h_1\).

La surface de la section du tube vaut: \(S=1\text{cm}^{2}=10^{-4}\text{m}^{2}\). Le volume ajouté est de: \(V_1=10\text{cm}^{3}=10^{-5}\text{m}^{3}\), or le volume est égale à la section fois la hauteur: \(V_1=S\times h_1\). On a donc:

\[\begin{split}h_1 &= \frac{V_1}{S}\\ h_1 &= \frac{10^{-5}}{10^{-4}}=0.1\text{m}=10\text{cm}\end{split}\]

2. En appliquant la relation fondamentale de l’hydrostatique, exprimer la différence de niveau \(\Delta h\) entre les deux surfaces libres, en fonction de \(\rho_e\), \(\rho_h\) et \(h_1\).

La ch8_tube_u_1 représente le montage, et introduit les points A, B et C qui désignent les différentes interfaces.

Schéma de l’expérience

• Le principe de l’hydrostatique appliqué entre les interfaces A et B (dans l’huile) s’écrit:

  \[p_A-p_B = -\rho_h g h_1\]

  avec \(p_A=p_{\text{atm}}\), soit finalement:

  ()\[p_B = p_{\text{atm}} + \rho_h g h_1\]

• Le principe de l’hydrostatique appliqué entre les interfaces C et B (dans l’eau) s’écrit:

  \[p_B-p_C = - \rho_e g h'\]

  avec \(p_C=p_{\text{atm}}\) et \(h'=h_1-\Delta h\), soit finalement:

  ()\[p_B = p_{\text{atm}} + \rho_e g (h_1 - \Delta h)\]

Les deux expressions de \(p_B\) données par les relations () et () doivent être égales:

\[\begin{split}p_{\text{atm}} + \rho_h g h_1 &= p_{\text{atm}} + \rho_e g (h_1 - \Delta h) \\ \Leftrightarrow \rho_h g h_1 &= \rho_e g (h_1 - \Delta h) \\ \Leftrightarrow \rho_h g h_1 &= \rho_e g h_1 - \rho_e g \Delta h \\ \Leftrightarrow \rho_e \Delta h &= (\rho_e - \rho_h) h_1 \\\end{split}\]

et finalement:

\[\boxed{\Delta h=\left(1-\frac{\rho_h}{\rho_e}\right)h_1}\]

Application numérique:

\[\begin{split}\Delta h&=\left(1-\frac{900}{1000}\right)\times 0.1\\ &= (1-0.9)\times 0.1\\ &= 0.01\text{m} \\ &= 1\text{cm}\end{split}\]

3. On ajoute ensuite \(V_2=20~\text{cm}^3\) de la même huile dans la branche de gauche. On note \(h_2\) la hauteur d’huile correspondante. Déterminer la nouvelle différence de niveau \(\Delta h'\) en fonction de \(\rho_e\), \(\rho_h\), \(h_1\) et \(h_2\).

La ch8_tube_u_2 représente le montage, et introduit le points D qui désignent la nouvelle interface huile/air. Cette fois \(p_C\neq p_{\text{atm}}\)

Schéma de l’expérience

• Le principe de l’hydrostatique appliqué entre les interfaces A et B (dans l’huile) s’écrit toujours:

  ()\[p_B = p_{\text{atm}} + \rho_h g h_1\]

• Le principe de l’hydrostatique appliqué entre les interfaces C et B (dans l’eau) s’écrit toujours:

  ()\[p_B = p_{C} + \rho_e g h' = p_{C} + \rho_e g (h_1 - \Delta h)\]

• Le principe de l’hydrostatique appliqué entre les interfaces D et C (dans l’huile) s’écrit:

  \[p_D-p_C = - \rho_h g h_2\]

  avec \(p_D=p_{\text{atm}}\), soit finalement:

  ()\[p_C = p_{\text{atm}} + \rho_h g h_2\]

  En combinant les relations () et () qui doivent être égale on obtient:

  \[p_{\text{atm}} + \rho_h g h' = p_C + \rho_e g (h_1-\Delta h)\]

  En remplaçant \(p_C\) par l’expression donnée dans la relation () on obtient:

  \[\begin{split}p_{\text{atm}} + \rho_h g h_1 &= \underbrace{p_{\text{atm}} + \rho_h g h_2}_{=p_C} + \rho_e g (h_1-\Delta h) \\ \Leftrightarrow \rho_e \Delta h &= \rho_h (h_2-h_1)+\rho_e h_1 \\\end{split}\]

  et finalement:

  \[\boxed{\Delta h = \frac{\rho_h}{\rho_e}(h_2-h_1) + h_1}\]

  Pour pouvoir faire l’application numérique il nous faut calculer \(h_2\). On sait que:

  \[V_2 = S h_2\]

  On déduit que:

  \[h_2=\frac{V_2}{S} = \frac{20\text{cm}^3}{1\text{cm}^2}=20\text{cm}\]

  Avertissement

  Attention aux unités: ici on divise des \(\text{cm}^3\) par des \(\text{cm}^2\) donc on obtient le résultat directement en \(\text{cm}\).

  Ce qui donne finalement:

  \[\Delta h= \frac{900}{1000} (0.2-0.1) + 0.1 = 0.19\text{m}=19\text{cm}\]

4. Modèle d’atmosphère isotherme \((\ast \ast \ast )\)

On tient compte dans cet exercice de la compressibilité de l’air afin de décrire l’évolution de la pression avec l’altitude \(z\). L’axe vertical \((Oz)\) est orienté vers le haut, l’altitude \(z=0\) correspondant au niveau du sol.

1. Rappeler la loi fondamentale de l’hydrostatique sous sa forme locale.

2. L’air étant considéré comme un gaz parfait, exprimer sa masse volumique \(\rho\) en fonction de \(p\), \(R\), \(T\) et \(M\) sa masse molaire.

3. Dans ce modèle, on suppose que la température est constante : \(T=T_0\). Montrer que la pression vérifie l’équation différentielle suivante : \(\frac{d p}{ d z} = - \frac{1}{\lambda} p(z)\), où \(\lambda\) est une constante que l’on déterminera. Quelle est sa dimension ? Faire l’application numérique pour \(T_0=293\) K, \(R=8,31~\text{J}\cdot \text{mol}^{-1} \cdot \text{K}^{-1}\) et \(M=29~\text{g} \cdot \text{mol}^{-1}\).

4. Résoudre l’équation différentielle avec la condition initiale \(p(0)=p_0\). Tracer la solution \(p(z)\). On fera figurer \(\lambda\) sur le graphique.

5. Pour des altitudes \(z \ll \lambda\), on peut remplacer la courbe de \(p(z)\) par sa tangente à l’origine [1]. En déduire une expression approchée de la pression lorsque \(z\) est petit. Commenter le résultat.

Solution

1. Rappeler la loi fondamentale de l’hydrostatique sous sa forme locale.

Nous avons vu en cours que l’équation de l’hydrostatique s’écrit:

\[\boxed{\frac{dp}{dz} =-\rho g }\]

2. L’air étant considéré comme un gaz parfait, exprimer sa masse volumique \(\rho\) en fonction de \(p\), \(R\), \(T\) et \(M\) sa masse molaire.

La masse volumique, exprimée pour une mole de gaz, vaut:

\[\rho=\frac{\text{masse d'une mole}}{\text{volume d'une mole}}=\frac{M}{V}\]

On connait la masse d’une mole (masse molaire) \(M\). Il reste à déterminer le volume d’une mole. Pour cela on utilise la loi des gaz parfaits:

\[\begin{split}p V &= n R T \text{ avec } n=1\text{mole} \\ \Leftrightarrow V = \frac{R T}{p}\end{split}\]

En combinant ces deux expressions on obtient:

\[\boxed{\rho=\frac{M p}{R T}}\]

3. Dans ce modèle, on suppose que la température est constante […]

On a: \(\parder{p}{z}=-\rho g\) et par ailleurs on a aussi \(\rho=\frac{M}{R T_0} p\). En combinant les deux on obtient:

\[\parder{p}{z}=-\frac{M g}{R T_0} p(z)\]

En posant \(\lambda=\frac{R T_0}{M g}\) l’expression précédente devient:

\[\parder{p}{z} = -\frac{1}{\lambda} p(z)\]

Le terme de gauche de cette équation différentielle a pour dimension \([\text{Pression}] \cdot [\text{Longueur}]^{-1}\).

Le terme de droite à pour dimension: \([\lambda]^{-1} \cdot [\text{Pression}]\)

En identifiant il vient que:

\[[\lambda]=L\]

On peut aussi le confirmer en regardant les unités des différents termes qui composent \(\lambda\):

• \(R\) est en \(J \cdot \text{mol}^{-1} \cdot K^{-1}=\underbrace{kg \cdot m^2 \cdot s^{-2}}_{=J} \cdot \text{mol}^{-1} \cdot K^{-1}\)

• \(T_0\) est en \(K\)

• \(M\) est en \(kg \cdot \text{mol}^{-1}\)

• \(g\) est en \(m \cdot s^{-2}\)

Donc:

\[\begin{split}\lambda &= \frac{R T_0}{M g} \\ &\Rightarrow \frac{kg \cdot m^2 \cdot s^{-2} \text{mol}^{-1} \cdot K^{-1} \cdot K}{kg \cdot \text{mol}^{-1} \cdot m \cdot s^{-2}} = m \\\end{split}\]

Application numérique:

\[\lambda=\frac{8.31\times293}{29\times10^{-3}\times9.81}=8558 m\]

4. Résoudre l’équation différentielle […]

Nous avons vu au Chapitre 3 que les équations différentielles du type : \(\parder{y}{t}=\alpha y(t)\) ont pour solution \(y=C e^{\alpha t}\).

Donc ici:

\[p=C e^{-\frac{1}{\lambda} z}\]

Pour \(z=0`on a :math:`p(0)=C=p_0\) et donc finalement:

\[\boxed{p=p_0 e^{-\frac{1}{\lambda} z}}\]

La Figure interactive ci-dessous montre graphiquement l’évolution de la pression avec l’altitude \(z\) entre 0 et 10000m.

(Source code, html)

5. Pour des altitudes \(z \ll \lambda\), on peut remplacer la courbe de \(p(z)\) par sa tangente à l’origine [1]_. En déduire une expression approchée de la pression lorsque \(z\) est petit. Commenter le résultat.

Lorsque \(z<<\lambda\) on peut faire l’approximation \(p(z) \approx p(0) + z p'(0)\).

Or \(p'(z)=-p_0 \frac{1}{\lambda} e^{-\frac{1}{\lambda} z}\), et donc \(p'(0)=-\frac{p_0}{\lambda}\).

Il vient alors:

\[\begin{split}p(z) &\approx p_0 -\frac{p_0}{\lambda} z \\ p(z) &\approx p_0 (1-\frac{1}{\lambda} z)\end{split}\]

A de faibles altitudes la pression varie quasiment linéairement.

On peut représenter cette droite sur le graphique précédent. On voit que l’approximation semble valable jusqu’à environ 1000m. Au delà les deux courbes divergent.

(Source code, html)

5. Flottabilité d’une planche de surf \((\ast )\)

On modélise une planche de surf par un parallélépipède rectangle de longueur \(L=2\) m, de largeur \(l= 50\) cm et d’épaisseur \(h=8\) cm. La planche est réalisée dans une mousse de masse volumique \(\rho_s= 50~\text{kg}\cdot \text{m}^{-3}\). On note \(\rho_m= 1040~\text{kg}\cdot \text{m}^{-3}\) la masse volumique de l’eau de mer.

1. On considère d’abord la planche posée à vide sur l’eau de mer. Exprimer la hauteur immergée \(h_i\) en fonction de \(h\), \(\rho_m\) et \(\rho_s\) . Faire l’application numérique.

2. Une personne de masse \(m\) se tient debout sur la planche. À partir de quelle masse \(m^{*}\) la planche atteint-elle la limite de flottaison \(h_i=h\) ?

Solution

1. Exprimer la hauteur immergée \(h_i\) en fonction de \(h\), \(\rho_m\) et \(\rho_s\) . Faire l’application numérique.

Puisque la planche de surf flotte, c’est que son poids est équilibré par la poussée d’Archimède:

\[\vec{\Pi} = \vec{P}\]

Or la poussée d’Archimède est égale (en norme) au poids du volume d’eau de mer déplacé (équivalent au volume \(V_{im}=L \times l \times h_i\) de planche immergé):

\[\begin{split}\vec{\Pi} &=- \rho_m V_{im} \vec{g} \\ &= -\rho_m L l h_i \vec{g}\end{split}\]

Le poids quant à lui vaut simplement: \(\vec{P}=m\vec{g}=\rho_s L \times l \times h \times \vec{g}\).

La relation \(\vec{\Pi} = \vec{P}\) peut donc s’écrire (en norme):

\[\begin{split}\rho_m L \times l \times h_i  g &= \rho_s L \times l \times h \times g\\ \Leftrightarrow h_i &= \frac{\rho_s}{\rho_m} h \\\end{split}\]

Application numérique:

\[h_i = \frac{50}{1040} \times 8 = 0.38\text{cm}\]

2. Une personne de masse \(m\) se tient debout sur la planche. À partir de quelle masse \(m^{*}\) la planche atteint-elle la limite de flottaison \(h_i=h\) ?

La limite de flottaison est atteinte quand le surf commence à couler, c’est à dire qu’il est complètement immergé et \(h_i=h\). On a alors, d’après le principe fondamental de la dynamique:

\[\vec{P} + m^{*} \vec{g} + \vec{\Pi} = \vec{0}\]

avec cette fois:

\[\begin{split}\vec{P} &=\rho_s V \vec{g} \\ \vec{\Pi} &= -\rho_m V \vec{g} \\\end{split}\]

et donc, en projetant sur l’axe vertical:

\[\begin{split}\rho_s V g + m^{*} g - \rho_m V g &= 0 \\ \Leftrightarrow m^{*} &= V (\rho_m-\rho_s)\\ \Leftrightarrow m^{*} &= L\times l \times h (\rho_m-\rho_s)\end{split}\]

Application numérique:

\[m^{*} = 2 \times 0.5 \times 0.08 (1040 -50)=79.2\text{kg}\]

Conclusion:

Votre professeur préféré coule lamentablement.

6. Balance hydrostatique \((\ast \ast)\)

Principe de fonctionnement d’une balance hydrostatique.

Pour déterminer la densité d’un solide, on peut utiliser une balance hydrostatique dont le principe de fonctionnement est illustré sur la ch8_balance. On note \(\rho_s\) la masse volumique du solide et \(\rho_e\) celle de l’eau.

• On suspend le solide sous le plateau de gauche et on équilibre le fléau en disposant des poids sur le plateau de droite. On mesure ainsi la masse \(M\) de l’objet.

• On plonge l’objet dans un récipient rempli d’eau. Le premier plateau remonte car le poids apparent de l’objet est inférieur dans l’eau que dans l’air.

• On équilibre alors le fléau en ajoutant une masse \(m\) sur le premier plateau (opération non représenté sur la figure).

À partir de ces observations, montrer que la masse \(m\) correspond exactement à la masse du volume d’eau déplacé. En déduire l’expression de la densité \(d=\rho_s/\rho_e\) du solide en fonction de \(M\) et \(m\).

Solution

1. À partir de ces observations, montrer que la masse \(m\) correspond exactement à la masse du volume d’eau déplacé.

• Sur le schéma de gauche, on peut déduire qu’à l’équilibre on a, en notant \(\vec{P_s}\) le poids du solide et \(\vec{P}\) le poids de la masse sur le plateau de droite:

  ()\[\vec{P_s} = \vec{P} \Leftrightarrow P_s = M g\]

• Sur le schéma de droite, en notant \(\vec{\Pi}\) la poussée d’Archimède et \(\vec{P}_{\text{suppl}}\) le poids supplémentaire ajouter au plateau de gauche pour revenir à l’équilibre:

  ()\[\vec{P_s} + \vec{\Pi} +\vec{P}_{\text{suppl}} = \vec{P}\]

  soit en projetant sur \((Oz)\):

  \[\begin{split}-P_s + \Pi - P_{\text{suppl}} &= -P \\ \Leftrightarrow -Mg + \rho_e V_i g -m g &= -Mg \\ \Leftrightarrow -M + \rho_e V_i -m &= -M \\ \Leftrightarrow \rho_e V_i -m &= 0\end{split}\]

  soit finalement:

  \[\boxed{m=\rho_e V_i}\]

2. En déduire l’expression de la densité \(d=\rho_s/\rho_e\) du solide en fonction de \(M\) et \(m\)

Par définition des masses volumiques, on peut écrire:

\[\begin{split}\begin{cases} M = \rho_s V \\ m = \rho_e V_i \end{cases} \Rightarrow d=\frac{\rho_s}{\rho_e}=\frac{M V_i}{m V}\end{split}\]

Lorsque l’objet est totalement immergé, alors \(V_i=V\) et on obtient:

\[\boxed{\frac{M}{m}}\]

2. En déduire l’expression de la densité \(d=\rho_s/\rho_e\) du solide en fonction de \(M\) et \(m\).

7. Ascension d’un ballon-sonde \((\ast \ast)\)

En météorologie, on utilise des ballons-sonde gonflés à l’hélium (\(\rho_{He}=0,2~\text{kg}\cdot\text{m}^{-3}\)) pour faire des mesures locales de l’atmosphère. Le ballon considéré ici est constitué d’une enveloppe inextensible, dont le volume maximum est \(V_{\textrm{max}}=30~\text{m}^3\). Le ballon transporte également des instruments de mesure. La masse de l’ensemble {ballon + instruments} est \(M=10\) kg.

1. On gonfle initialement la ballon avec un volume \(V_0\) d’hélium. Exprimer la masse \(m\) d’hélium contenue dans le ballon.

2. Faire le bilan des forces qui s’exercent sur le système {ballon + instruments + hélium}. En déduire la valeur minimale de \(V_0\) pour que le ballon s’envole. On négligera le volume des instruments. Faire l’application numérique.

On suppose que l’air est un fluide incompressible (\(\rho_{\textrm{air}}=1,2~\text{kg}\cdot\text{m}^{-3}\)), et que la température est constante:  \(T_0=300\) K. Au cours de l’ascension, la pression de l’hélium contenu dans le ballon est égale à la pression de l’air à l’extérieur.

3. Déterminer la loi d’évolution \(p(z)\) de la pression de l’air avec l’altitude \(z\). Pour la pression au sol, on prendra : \(p(0)=p_0 = 10^5\) Pa.

4. En appliquant la loi des gaz parfait, montrer que le volume du ballon varie avec l’altitude selon la loi : \(V(z) = \frac{V_0}{1-z/z_0}\)

   où \(z_0\) est une constante que l’on déterminera. Quelle est la dimension de \(z_0\) ? Faire l’application numérique. Tracer la courbe \(V(z)\).

5. Étant donné la valeur de \(V_{\textrm{max}}\), déduire l’altitude maximale atteinte par le ballon.

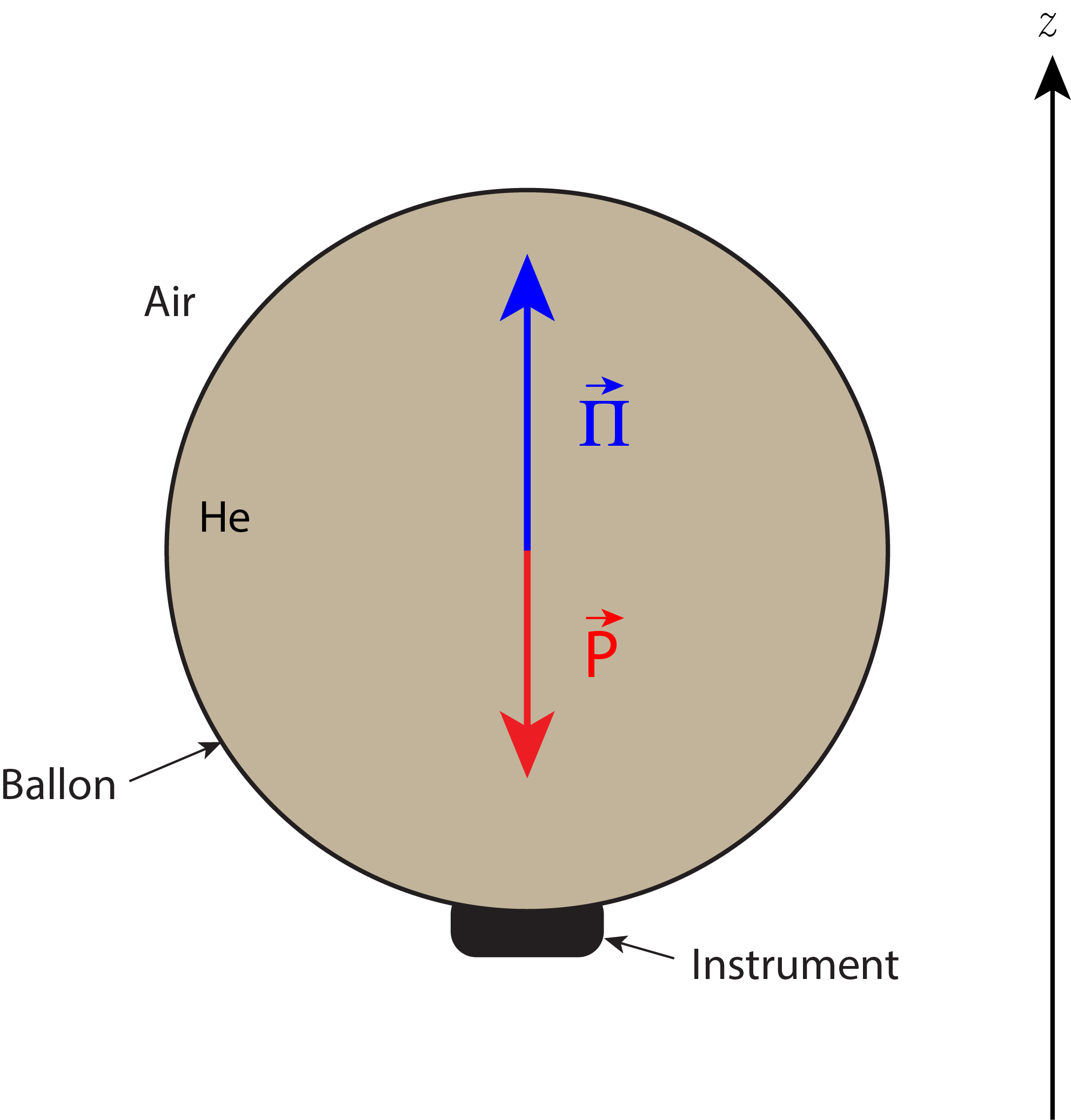
Schéma du ballon sonde

Solution

1. On gonfle initialement la ballon avec un volume \(V_0\) d’hélium. Exprimer la masse \(m\) d’hélium contenue dans le ballon.

La masse est donnée simplement par le produit de la masse volumique par le volume du ballon:

\[m = \rho_{\text{He}} V_0\]

2. Faire le bilan des forces qui s’exercent sur le système {ballon + instruments + hélium}. En déduire la valeur minimale de \(V_0\) pour que le ballon s’envole. On négligera le volume des instruments. Faire l’application numérique.

Le biland des forces qui s’appliquent inclue:

• le poids du système {ballon + instruments + hélium} \(\vec{P}\)

• la poussée d’Archimède de l’air \(\vec{\Pi}\)

On cherche le volume minimal \(V_0\) tel que \(\Pi\ge P\). À l’équilibre, on a \(\vec{P} + \vec{\Pi} = \vec{0}\). En projetant sur l’axe \((Oz)\), on obtient:

\[-P + \Pi=0 \Rightarrow P=\Pi\]

avec:

• \(\Pi=\rho_{\text{air}} V_0 g\)

• \(P=(M+\rho_{\text{He}} V_0) g\)

Donc on doit avoir:

\[\begin{split}\rho_{\text{air}} V_0 g \ge (M+\rho_{\text{He}} V_0) g \\ \Leftrightarrow \rho_{\text{air}} V_0 \ge (M+\rho_{\text{He}} V_0) \\ \Leftrightarrow V_0 (\rho_{\text{air}} - \rho_{\text{He}}) \ge M\end{split}\]

soit finalement:

\[\boxed{V_0\ge \frac{M}{\rho_{\text{air}} - \rho_{\text{He}}}}\]

3. Déterminer la loi d’évolution \(p(z)\) de la pression de l’air avec l’altitude \(z\). Pour la pression au sol, on prendra: \(p(0)=p_0 = 10^5\) Pa.

On a:

\[\frac{dp}{dz}=-\rho_{\text{air}} g \Rightarrow p = -\rho_{\text{air}} g z + C\]

Pour trouver la constante on note que pour \(z=0\) on a \(p(0)=p_0\), et donc:

\[\boxed{p = p_0 -\rho_{\text{air}} g z}\]

4. En appliquant la loi des gaz parfait, montrer que le volume du ballon varie avec l’altitude selon la loi: \(V(z) = \frac{V_0}{1-z/z_0}\)

La loi des gaz parfaits s’écrit ici: \(pV=nR T_0 = P_0 V_0\)

Donc:

\[\begin{split}V&=\frac{n R T_0}{p} \\ &= \frac{nRT_0}{p_0 -\rho_{\text{air}} g z}\end{split}\]

Or: \(nRT_0 = p_0 V_0\), donc:

\[\begin{split}V &=\frac{p_0 V_0}{p_0 -\rho_{\text{air}} g z} \\ &= \frac{V_0}{1-\frac{\rho_{\text{air}} g z}{p_0}} \\ &= \frac{V_0}{1-\frac{z}{z_0}} \text{ avec } z_0=\frac{p_0}{\rho_{\text{air}} g}\\\end{split}\]

Comme \(nRT_0 = p_0 V_0\), on peut aussi écrire:

\[\boxed{z_0=\frac{n R T_0}{\rho_{\text{air}} g V_0}}\]

La dimension de \(z_0\) est donc:

\[[z_0]=\frac{[p]L^3 T^2}{M L}\]

avec pour la pression: \([p]=\frac{[\text{Force}]}{\text{[Surface]}}=\frac{MLT^{-2}}{L^2}=\frac{ML}{T^2}\)

Donc finalement:

\[[z_0]=\frac{M L T^{-2} L^3 T^2}{M L} [z_0]=L\]

Application numérique:

\[z_0=\frac{10^5}{1.2\times9.81}=8495\text{m}\]

(Source code, html)

5. Étant donné la valeur de \(V_{\textrm{max}}\), déduire l’altitude maximale atteinte par le ballon.

Pour \(V=V_{\rm{max}}\) alors:

\[\begin{split}V &=V_{\rm{max}} = \frac{V_0}{1-\frac{z_{\rm{max}}}{z_0}} \\ \Rightarrow z_{\rm{max}} &= z_0\left(1-\frac{V_0}{V}\right) z_{\rm{max}} &= 8495 \times \left(1-\frac{10}{30}\right)=5667\text{m}\end{split}\]

[1]

Pour \(x\) petit, on peut écrire : \(f(x) \approx f(0) + xf'(0)\).